基于相角超前补偿网络的DC/DC变换器数模混合补偿方法

佟 强张东来徐殿国

(1. 哈尔滨工业大学深圳研究生院 深圳 518055 2. 哈尔滨工业大学电气工程与自动化学院 哈尔滨 150001)

基于相角超前补偿网络的DC/DC变换器数模混合补偿方法

佟 强1张东来1徐殿国2

(1. 哈尔滨工业大学深圳研究生院 深圳 518055 2. 哈尔滨工业大学电气工程与自动化学院 哈尔滨 150001)

相对于模拟控制方式，数字控制 DC/DC变换器由于反馈回路中存在着固有的延迟效应，动态性能通常不如模拟控制的 DC/DC变换器。提出了一种数模混合的控制器补偿方法，它基于相角超前校正网络来提高系统的相角裕量，从而减小输入电压波动或负载跃变时输出电压的波动幅值。搭建了一个基于 FPGA平台的数字控制同步 Buck变换器，将所提的方法与几种传统的电压控制型数字控制补偿方法进行对比。实验表明数模混合补偿方法具有电路简单、动态特性好的优点，方便和现有的商用数字电源控制芯片结合以提高电源的动态响应能力。

数字控制 DC/DC变换器 小信号离散时间模型 高动态响应 数模混合控制 相角超前补偿

1 引言

数字控制DC/DC变换器多应用于负载点电源，其动态响应能力是一项很重要的指标[1-2]。尤其重要的是要确保负载变化时，输出电压的超调量较小，以保证通信和数据处理系统中的控制器从待机状态到满负荷工作状态切换时能快速可靠地工作。

目前提高数字控制 DC/DC变换器动态性能的方法有拓扑结构的改进和数字控制器的改进，其中数字控制器改进方法概括起来可分为四种：第一种是在传统数字控制器的基础上利用数字控制的灵活性，调整控制参数或改变补偿器形式，以使系统达到较高的带宽[3-4]。此种方式容易实现，但受数字控制器结构限制以及数字控制系统中的延迟效应影响，对系统的动态响应能力提高程度有限。第二种控制方法是基于自适应PID和模糊PID的原理[5-9]，对应电源的不同工作状态设计不同的PID参数。在电源实际工作的时候，控制器可以根据电源的工作情况自动实现参数切换，使电源在整个工作范围都能达到较好的动态特性。此种方式的缺点是控制器的程序较复杂，控制参数较多，运算量大。同时也仍然受到数字控制中延迟效应的影响。第三种改进方法是加入电流反馈构成电压-电流双环控制[10]。当输入电压或负载电流变化时，电流环路可以快速反应，无需等到最终输出电压变化时才开始调节，因此动态响应能力明显好于电压反馈单环控制。然而增加电流反馈回路就要相应地在电路中加入无感电流取样电阻、高带宽的电流检测运放和A/D转换器，使得电源的成本大大提高。因此目前商用的小功率数字DC/DC变换器多以电压单环控制为主。第四种改进方法是在数字控制器中加入非线性控制，构成混合模式控制器[11-16]。当电源工作在动态条件时，非线性控制器发挥作用，可显著提高系统的动态响应能力。这些控制器有的在一定条件下会造成电源不稳定[16]，有的需要高成本的电流放大器来测量输出电容电流[15]。总的来说，这些混合控制补偿器的复杂程度和成本都已经远超过了传统的PWM控制器，因此没有在高频小功率开关电源中广泛应用。

目前各主要电源芯片制造商都已推出专属的数字电源控制芯片，这些电源芯片内部的补偿器类型都已固定，用户只能根据需要对补偿器参数进行调整。本文基于相角超前校正原理提出了一种数模混合控制相结合的补偿器设计方法，方便和现有的数字DC/DC控制芯片结合，通过加入模拟补偿网络提高了补偿器的阶数，使系统的动态响应能力得到提升。本文首先给出了数模混合控制电源系统的整体结构，描述了数模混合补偿器的设计思路和方法，以一个 RC相角超前补偿电路为例详细论述了数模混合控制器中模拟补偿部分的设计方法和参数优化方法。其次，通过仿真的方法对几种常用的数字补偿器[3,17-18]和本文提出的数模混合补偿器控制下电源系统的环路特性进行对比分析。最后，通过一个基于 FPGA控制的数字 DC/DC变换器平台对本文所提的方法以及本文所举例的其他几种数字补偿方法进行对比。

2 数模混合补偿器的设计方法

2.1 采用数模混合补偿器的电源整体结构

提高系统动态响应速度最直接的办法就是提高系统控制环路的穿越频率。数字控制系统中受数字补偿器结构的限制，提高穿越频率会降低系统的相角裕量，造成系统稳定性下降甚至不稳定。提高系统的相角裕量可以提高系统的稳定性，减小负载切换时输出电压的波动幅值，同时为进一步提高系统的穿越频率创造条件，使系统有更快的调整速度，是提高系统动态响应的最佳方法[19-20]。本文提出的数模混合补偿器的设计思路就是在那些补偿器类型已经固定的数字控制电源中加入模拟补偿环节，提高补偿器整体的阶数，使电源的动态响应速度得到提高。

模拟电路校正网络加在拓扑输出电压与A/D采样环节之间，与变换器原来的数字补偿网络串联在一起，形成了一个新的数模混合补偿网络。加入相角超前校正网络后的系统框图如图1所示。

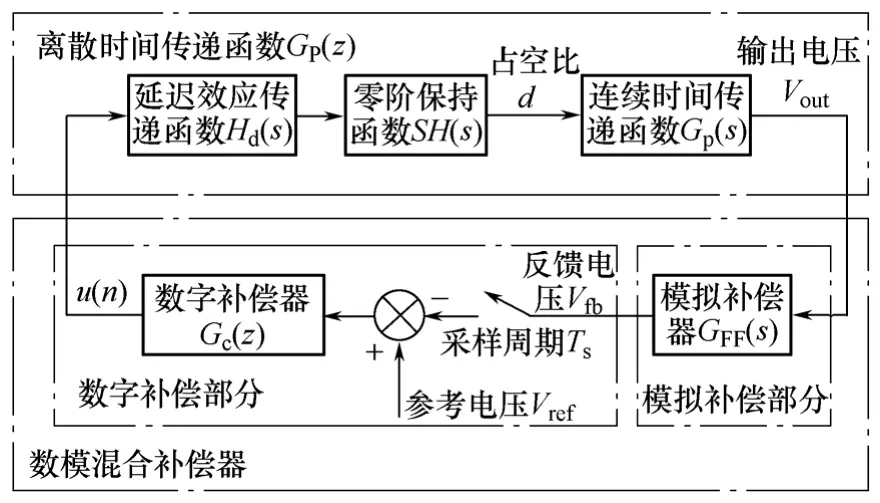
图1 数模混合控制系统的控制框图Fig.1 The analog-digital mixed compensation control loop block diagram

设计数模混合补偿器时，首先要设计数字补偿部分，然后再设计模拟补偿部分。其中数字补偿部分要对被控系统进行离散化处理，得到离散时间传递函数，然后在频域范围完成数字补偿器的设计[21-25]。设计模拟补偿部分的时候先将整个数字控制电源看作一个整体，其特性可以用连续时间函数来表示，然后根据实际需要在时域范围完成模拟补偿器的设计。它可以是由电阻电容构成的无源补偿网络，也可以是由运算放大器构成的有源补偿网络，目的都是为了在数字控制的基础上进一步提高系统控制环路中穿越频率附近的相角裕量。

2.2 模拟补偿部分的设计与参数优化

本文以一个 RC相角超前校正电路为例说明此补偿器的设计和优化过程，电路如图2所示。

此补偿电路的传递函数为

式中

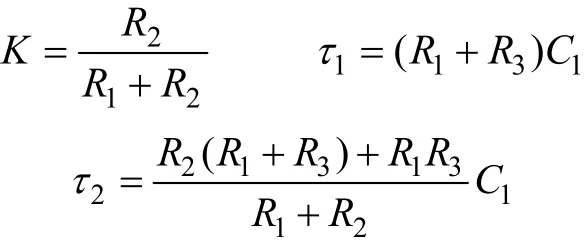
它是单零点单极点补偿网络，零点频率fz=1/τ1，极点频率 fp=1/τ2。因为τ2＜τ1，所以零点频率低于极点频率，因此它是一个相角超前校正网络，对应的博德图如图3所示。

图3 相角超前校正网络博德图Fig.3 Bode plot of the phase lead compensation

从图3可见，在所加的零点频率之前，相角就已经开始增加，在fz和fp之间相角达到最大。因此在略高于系统原穿越频率处加入此相角超前网络，既可以提高相角裕量，又保持增益曲线以−20dB/dec斜率穿越0dB。此补偿网络的相角与频率关系为

若原系统的穿越频率为 10kHz，后加入的零点和极点频率设定为20kHz和40kHz，则加入此相角超前网络后在10kHz处提升的相角为

通过式（2）可以定量地计算在一个固定的频率点（例如穿越频率）下，R3、C1取值与提升的相角之间的关系。设定R3的取值为0～1kΩ，C1的取值为0.1nF～1µF，在10kHz频率下此超前校正网络对相角的提升如图4所示。

图4 超前校正网络参数与相角提升角度关系Fig.4 The relationship between the parameters of compensation circuit and the boosted angle

从图4可以看出R3的取值对相角的提升帮助较大，电容C1的取值对相角的提升影响很小。在模拟控制方式中不可避免地存在着模拟器件参数漂移的问题，图4也可以表示模拟补偿网络中电阻和电容发生器件参数漂移时，补偿网络特性的变化。若取R3=100Ω，C1=1nF，理论上在10kHz频率处可以提升的相角度数为 40°。如果模拟补偿器选择此参数，则系统频率与提升的相角的对应关系如图5所示。

图5 补偿器提升角度与频率的对应关系Fig.5 The relationship between boosted angle and frequency

从图5可以看到此组参数在整个频率范围提升系统的相角裕量，尤其是在穿越频率附近，相角提升度数达到最大，因此可确定这组参数为最优参数。

根据式（1）此参数下模拟部分的传递函数为

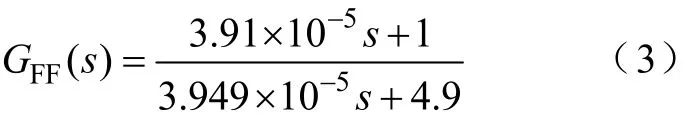
此模拟补偿网络与数字补偿器一起构成数模混合补偿网络。它的设计原则是，数字补偿器首先对被控拓扑进行补偿，主要是抵消被控对象传递函数中存在的零点和极点。利用数字补偿器的灵活性可以解决拓扑参数漂移所带来的零极点漂移问题。模拟补偿网络只是用来提升穿越频率附近的相角裕量，并不要求较高的精确度。因此模拟器件的参数误差或温漂，对整体的控制效果有一定的影响。从图4也可以看出电阻R3在60～200Ω范围之内变化均可以将相角提高 38°以上，而实际应用中 R3的阻值漂移范围也不会这么大。在数字电源的反馈回路加入模拟补偿环节，构成数模混合补偿器可以弥补单一补偿器的不足，可显著提高数字系统的性能。

3 数模混合补偿器与其他几种常用数字补偿器的仿真对比

在进行数字补偿器设计的时候首先要确定被控对象的离散时间传递函数。在考虑了采样保持效应和延迟效应之后，如图1中被控对象的离散时间传递函数为[22]

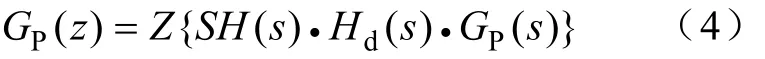
式中 GP(s)—变换器的连续时间小信号传递函数；

SH(s)—ADC与DPWM一起形成的采样保

Hd(s)—延迟效应传递函数

Ts—PWM信号的周期时间；

Td—数字控制中存在的总延迟时间。

图6描述了 DPWM与输出电压变化量的对应关系，可对数字控制中存在的延迟时间进行解释。t0时刻数字控制芯片的DPWM更新占空比，输出电压随之逐渐增大，在t1时刻控制A/D采样开始，t1要尽量避开拓扑开关开通或关断的时刻，因为在开关管开关时输出电压上有较大的开关噪声，会使采样的电压受到干扰。经过Tadc时间，在t2时刻A/D转换完成并将采样的电压值送给补偿器计算。又经过Tc时间，补偿器将计算所得的占空比送到DPWM模块，并在下一个开关周期t3时刻更新占空比。从A/D采样时刻开始一直到发出 DPWM信号所用的延迟为Td=Tadc+Tc。

图6 数字控制DC/DC变换器采样及DPWM时序关系图Fig.6 DC/DC converter digital control loop sampling scheme

对于同步 Buck拓扑，连续时间小信号传递函数为

本文以一个额定功率为 20W 的数字电源系统为例进行研究。其最高输入电压 Vin=20V，输出电压Vo=5V，额定负载RL=1.25Ω，输出滤波电感14µH，输出滤波电容为200µF，等效串联电阻RC=20mΩ，开关频率为 300kHz。本系统中，A/D采样时刻 t1设定在DPWM信号发出700ns之后开始，因此A/D转换延迟、计算延迟总和为 Td=2600ns，在 Matlab中完成时域到频域的转换，采用零阶保持（ZOH）方法，由式（1）可得此时的拓扑离散时间传递函数为

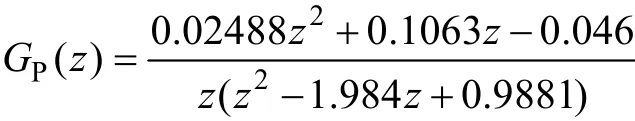
首先采用两极点两零点[17-18]补偿器对被控对象进行校正，它是目前大多数数字电源芯片采用的补偿器形式，具有典型性。两极点两零点补偿器在低频段设置一个极点使系统在低频段有−20dB的斜率，两个零点用来补偿 LC滤波器的二阶极点，另外一个极点用来补偿输出电容的等效串联电阻产生的高频零点。两极点两零点补偿器传递函数 GC1(z)为

数模混合补偿器是在两极点两零点补偿器GC1(z)的基础上进行设计的，对于校正后的系统，T1(z)首先转化为连续时间函数T1(s)，然后再进行补偿器中模拟部分的设计。模拟补偿器采用 2.2节中的结构，取值仍然为R3=100Ω，C1=1nF，对应的传递函数为式（3），校正后系统在连续时间内的传递函数为T2(s)=T1(s)GFF(s)。

三极点三零点的数字补偿器是在两极点两零点补偿器的基础上再加入一对零极点，这对零极点的位置可与模拟补偿网络中零极点的位置一致，以使两者的传递函数尽量一致。此三极点三零点补偿器传递函数GC3(z)为

图7对这三种补偿器校正后所得的系统开环博德图进行对比。在中频段（4～30kHz），两极点两零点补偿器下系统的相角裕量最低。数模混合补偿器和三极点三零点补偿器下系统的相角裕量得到明显的提高，两者的补偿效果基本一致。因此，在相同的穿越频率下，它可以大大降低电源输出电压的波动幅值。在满足稳定性要求的同时也可以尽量提高穿越频率，使电源有较快的调整速度。表1对比了三种补偿器下系统在相同频率处的相角和增益值，可以看到数模混合补偿器达到了三阶补偿器的补偿效果。

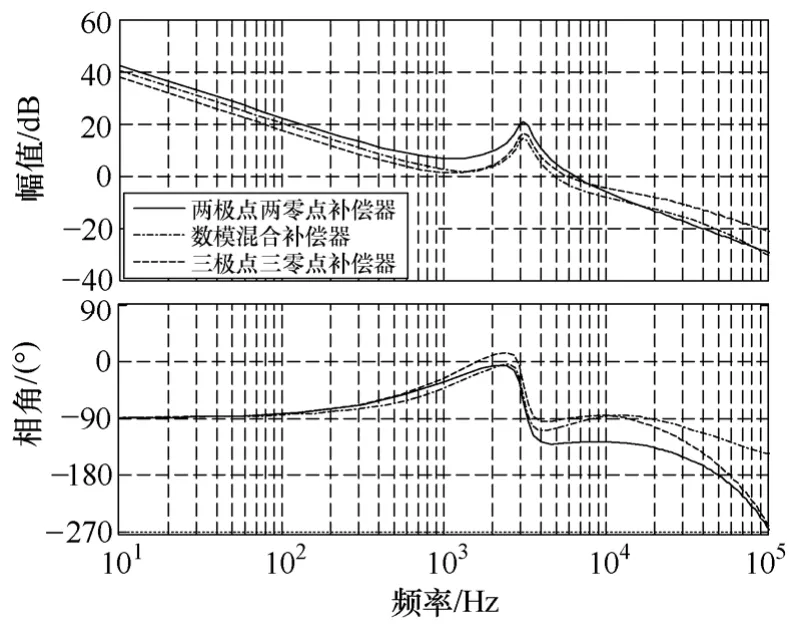
图7 三种补偿器下系统博德图的对比Fig.7 Comparison of Bode plots of systems with three different compensators

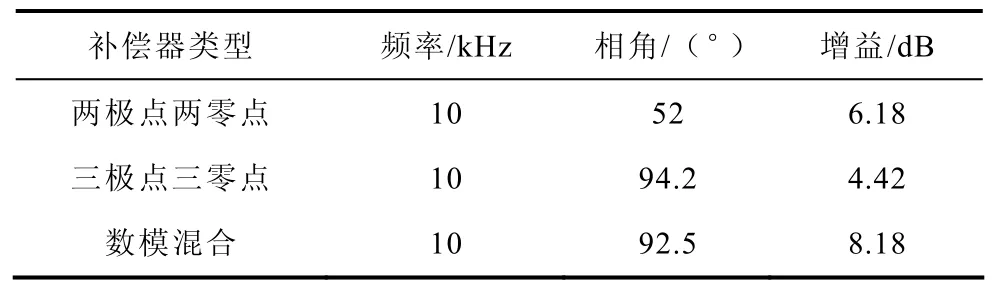
表1 三种补偿器下系统的环路参数对比Tab.1 Comparison of the control loop features of systems with three different compensators

4 实验验证

本文采用ALTERA公司CycloneII系列型号为EP2C35的 FPGA实现了一款数字控制输出功率为20W的DC/DC电源，指标参数如第3节所述。A/D的采样位数为10位，DPWM的精度为11位，避免了极限环振荡的产生[26]。采用菊水（KIKUSUI）公司型号为 PLZ664WA的电子负载和 NF公司的FRA5097频率特性分析仪。

图8和图9分别对两极点两零点补偿器和数模混合补偿器下系统的实测增益和相角博德图进行对比，可以看出采用数模混合控制器系统在穿越频率附近的相角裕量得到较大提升，实测结果与仿真分析结果一致。

图8 两种补偿器下系统实测增益的对比Fig.8 Comparison of gain of systems with two different compensators

图9 两种补偿器下系统实测相角的对比Fig.9 Comparison of phase of systems with two different compensators

对于DC/DC变换器，输入电压切换或负载电流切换都可以反映电源的动态响应能力。本文首先选择负载电流切换实验对这三种补偿器下电源系统的动态响应能力进行对比，控制电子负载的电流在0.4A和1.8A之间切换，切换斜率为2A/µs。输出电压波形如图10～图12所示。

表2给出了三种补偿器的特性以及实验测试结果，通过对比可以看出数模混合补偿器的动态特性与三极点三零点补偿器的动态性能接近，它的输出电压切换峰-峰值以及恢复时间都较小。

表2 三种补偿器下系统负载切换实验对比Tab.2 Comparison of load transient response of the power supply with the three different compensators

然后选择输入电压切换实验对这三种补偿器下电源系统的动态响应能力进行对比，设定输入电压在13V和20V之间切换，三种补偿器下变换器的输出电压波形如图13～图15所示。

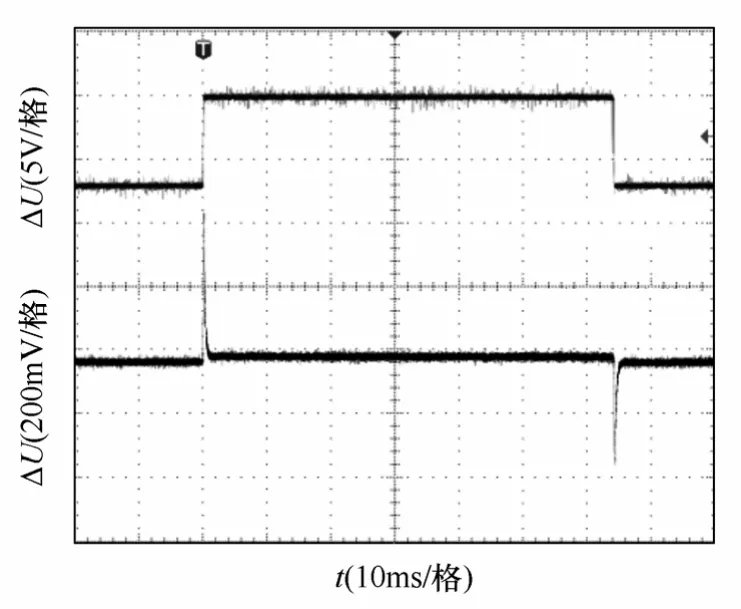
图13 采用两极点两零点补偿器时输出电压的响应Fig.13 Output voltage response with the 2-pole 2-zero compensator

图14 采用三极点三零点补偿器时输出电压的响应Fig.14 Output voltage response with the 3-pole 3-zero compensator

相同的输入电压切换条件下，采用三极点三零点补偿器和数模混合补偿器控制，变换器输出电压的波动幅值明显小于两极点两零点补偿器下输出电压的波动幅值。这与负载电流切换时所得的结果一致。

图15 采用数模混合补偿器时输出电压的响应Fig.15 Output voltage response with the analog-digital mixed compensator

数模混合补偿器可以利用数字控制的灵活性进一步提高系统的穿越频率，以得到更快的动态响应速度。保持模拟补偿网络参数不变，提高数字控制器中补偿器的增益系数可以提高系统的穿越频率。图16是提高了穿越频率后系统的实测博德图，相同负载切换条件下的输出电压波形如图17所示，可以看到输出电压的波动峰-峰值进一步减小，调整速度也得到提高，使系统达到最佳动态性能。

图16 采用提高了穿越频率的数模混合补偿器后系统实测博德图Fig.16 Bode plot of the system adopted analog-digital mixed compensator with higher crossover frequency

5 结论

本文针对低压大电流供电系统中对负载点电源动态性能的需求，提出了一种基于相位超前校正原理的数模混合补偿器设计方法。它方便和现有的数字电源控制芯片结合以提高补偿器的阶数，可以显著提高系统的相角裕量，使系统达到更好的动态性能。模拟器件组成的相角超前网络与数字控制器结合，根据系统性能需求可对每一部分进行优化设计，以使控制效果达到最佳。它既具有模拟控制结构简单、调整速度快的优点又具有数字控制设计灵活、参数可调的优点。在一个基于FPGA平台的数字电源上与其他几种数字补偿方式进行对比验证，结果表明数模混合补偿器可以使电源系统达到最优的动态性能。

图17 提高穿越频率后系统的负载切换响应Fig.17 Load transient response of the system adopted analog-digital mixed compensator with higher crossover frequency

[1] Rozman A, Fellhoelter K. Circuit considerations for fast, sensitive, low-voltage loads in a distributed power system[C]. IEEE APEC, 1995, 5: 33-42.

[2] Zhang M, Jovanovic M, Lee F C. Design considerations for low-voltage on-board DC/DC modules for next generations of data processing circuits[J]. IEEE Transactions on Power Electronics, 1996, 11: 328-337.

[3] Takayama T, Maksimovic D. Digitally controlled 10MHz monolithic Buck converter[C]. IEEE COMPEL, 2006: 154-158.

[4] Kurokawa F, Mizoguchi T. A smart control approach for digitally controlled multiple-output DC-DC converter[C]. IEEE PEDS, 2009: 405-410.

[5] Miao B, Zane R, Maksimovic D. System identifycation of power converters with digital control through cross-correlation methods[J]. IEEE Transactions on Power Electronics, 2005, 20(5): 1093-1099.

[6] Zhao Z Y, Prodic A, Mattavelli P. Self programmable PID compensator for digitally controlled SMPS[C]. IEEE COMPEL, 2006: 112-116.

[7] Stefanutti W, Mattavelli P, Saggini S, et al. Autotuning of digitally controlled DC-DC converters based on relay feedback[J]. IEEE Transactions on PowerElectronics, 2007, 22(1): 199-207.

[8] Mattavelli P, Rossetto L, Spiazzi G, et al. General purpose fuzzy controller for DC-DC converters[J]. IEEE Transactions on Power Electronics, 1997, 12(1): 79-86.

[9] Guo L P, Hung J Y, Nelms R M. Evaluation of DSP-based PID and fuzzy controllers for DC-DC converters[J]. IEEE Transactions on Industrial Electronics, 2009, 56(6): 2237-2248.

[10] Peng H, Maksimovic D. Digital current-mode controller for DC-DC converters[C]. IEEE APEC, 2005: 899-905.

[11] Zhao Z Y, Prodic A. Continuous-time digital controller for high-frequency DC-DC converters[J]. IEEE Transactions on Power Electronics, 2008, 23(2): 882-886.

[12] Hu H, Yousefzadeh V, Maksimovic D. Nonlinear control for improved dynamic response of digitally controlled DC-DC converters[C]. IEEE PESC, 2006: 1-7.

[13] Barrado A, Lazaro A, Pelite J, et al. Linear-non-linear control(LnLc) for DC/DC buck converters: stability and transient response analysis[C]. IEEE APEC, 2004, 2: 1329-1335.

[14] Soto A, Alou A P, Cobos J A. Nonlinear digital control breaks bandwidth limitations[C]. IEEE APEC, 2006: 42-47.

[15] Feng G, Meyer E, Liu Y F. Novel digital controller improves dynamic response and simplifies design process of voltage regulator module[C]. IEEE APEC, 2007: 1447-1453.

[16] Banerjee S, Verghese G C. Nonlinear phenomena in power electronics: attractors, bifurcation, chaos, and nonlinear control[M]. New Jersey: Wiley-IEEE Press, 2001.

[17] Lukic Z, Wang K, Prodic A. High-frequency digital controller for DC-DC converters based on multi-bit∑-Δ pulse-width modulation[C]. IEEE APEC, 2005: 35-40.

[18] Patella B J, Prodic A, Zirger A, et al. High-frequency digital PWM controller IC for DC-DC converters[J]. IEEE Transactions on Power Electronics, 2003, 18(1): 438-446.

[19] Marty Brown. 开关电源设计指南[M]. 徐德鸿, 等译. 北京: 机械工业出版社, 2004.

[20] Gene F Franklin, David Powell J, Abbas Emami Naeini. Feedback control of dynamic systems[M]. New Jersey: Prentice Hall, 2006.

[21] Franklin G F, Powell J D. Digital control of dynamic systems[M]. Boston, MA: Addision-Wesley Publishing Company, 1998.

[22] Van de Sype D M, Gusseme K D, Van den Bossche A P, et al. Small-signal z-domain analysis of digitally controlled converters[C]. IEEE PESC, 2004: 4299-4305.

[23] Prodic A, Maksimovic D, Erickson R W. Design and implementation of a digital PWM controller for a high-frequency switching dc-dc power converter[C]. IEEE IECON, 2001: 893-898.

[24] 姚雨迎, 张东来, 徐殿国. 级联式DC/DC变换器输出阻抗的优化设计与稳定性[J]. 电工技术学报, 2009, 24(3): 147-152. Yao Yuying, Zhang Donglai, Xu Dianguo. Output impedance optimization and stability for cascade DC/DC converter[J]. Transactions of China Electrotechnical Society, 2009, 24(3): 147-152.

[25] Maksimovic D, Zane R. Small-signal discrete-time modeling of digitally controlled dc-dc converters[J]. IEEE Transactions on Power Electronics, 2007, 22(6): 2552-2556.

[26] Peterchev A, Sanders S. Quantization resolution and limit cycling in digitally controlled PWM converters[J]. IEEE Transactions on Power Electronics, 2003, 18(1): 301-308.

Analog-Digital Mixed Compensator of DC/DC Converter Based on Phase Lead Compensation

Tong Qiang1Zhang Donglai1Xu Dianguo2
(1. Harbin Institute of Technology Shenzhen Graduate School Shenzhen 518055 China 2. Harbin Institute of Technology Harbin 150001 China)

The dynamic performance of digital controlled DC/DC converter is not as good as analog controller since there exits intrinsic delay in digital control loop. An analog-digital mixed compensation method to improve the dynamic performance of DC/DC converter is presented in this paper. It is based on phase lead compensation to boost the phase margin. So the peak to peak output voltage deviation due to changes of load current or line voltage can be decreased. A digital controlled synchronous Buck converter prototype was built. Performance of the converter with different voltage-mode compensators were tested and compared. It is demonstrated that the analog-digital mixed compensator has merits of simplicity and good dynamic performance. It can be applied with the commercial digital controller chip to further improve the dynamic performance of DC/DC converters.

Digital controlled DC/DC converters, small-signal discrete-time model, high dynamic performance, analog-digital mixed compensation, phase lead compensation

TM46

佟 强 男，1982年生，博士研究生，研究方向为开关变换器的模拟和数字控制技术，分布式电源系统。

2009-12-20 改稿日期 2010-06-15

张东来 男，1973年生，教授，博士生导师，研究方向为电力电子与电力传动、无损检测和数字信号处理等。