反渗透膜元件标准化产水量数学模型的优化

罗美莲，靖大为，朱建平，严丹燕，杨小奇

(天津城市建设学院 膜技术研究中心，天津 300384)

近年来，反渗透技术得到了快速发展，被广泛应用于市政、电力、石油、化工、冶金、电子、医药、食品等行业.在反渗透膜系统运行过程中，准确判断膜污染是保证系统稳定、高效运行的重要环节[1].膜污染直接影响反渗透系统的产水量这一重要测试指标.同时，给水温度、给水压力、回收率、给水盐浓度等运行条件的变化也会引起产水量的变化[2].例如，给水温度的变化不仅影响水的黏度，也影响膜的透水速率[3]；给水压力的变化直接影响产水的纯驱动压[4]；给水含盐量与回收率的变化直接影响膜元件给/浓水平均含盐量，间接影响产水的纯驱动压[5].

通过产水量指标的变化了解膜元件的污染程度，需剔除运行条件变化的影响.将不同运行条件下的实测产水量进行标准化处理，即将不同的运行条件折算为选定的标准条件，标准化后的计算结果即为标准化产水量[6].标准化产水量与标准条件下测试所得的标态产水量的差值就是膜污染程度的直接反映.本文以广为应用的某反渗透膜元件标准化产水量模型为基础，分析模型的计算精度，并为提高其精度对模型加以修正.

1 标准化产水量模型

计算反渗透膜元件标准化产水量 Qpn(m3/h)涉及给水温度T(℃)、给水盐浓度Cf(mg/L)、淡水盐浓度Cp(mg/L)、给水压力 Pf(MPa)、浓水压力 Pc(MPa)、淡水压力 Pp(MPa)、淡水流量 Qp(m3/h)、浓水流量Qc(m3/h)八个参数.某公司标准化产水量的数学模型如式(1)，其中下标含 r为标准条件下的相应值，下标含n为标准化模型计算的相应值.

式中：温度校正系数

净驱动压力

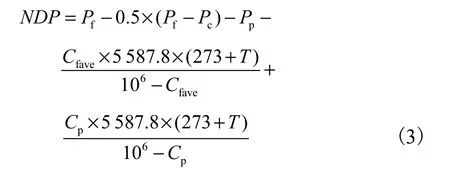
给/浓水平均盐浓度

给水盐浓度校正系数

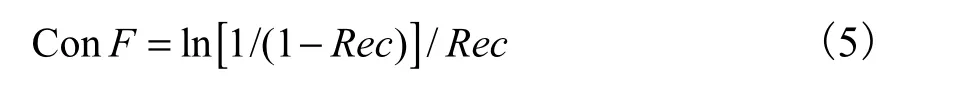
回收率

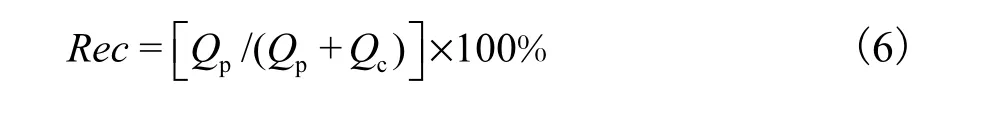
2 标准化模型计算结果准确性的检验

选择膜元件未有任何污染时的状态进行模型计算结果准确性的检验.此时计算结果的理想状况是：不同运行条件下计算出的标准化产水量 Qpn应与标准条件下的标态产水量 Qpr相等.本文以偏差比作为评价模型计算结果准确性的指标，标准化产水量的偏差比为

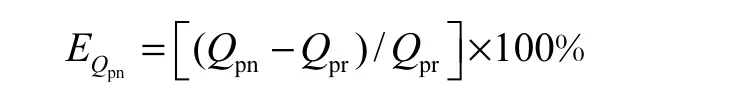
同样，不同运行条件下膜元件的实测产水量 Qp的偏差比为

由于实验条件难以精确控制，测量结果也存在误差，为使分析数据有较高的精度，采用已被广泛使用的某公司设计软件的计算数据替代工程实验数据.以下计算分析以ESPA3膜元件为例，取膜元件出厂测试条件为标准状态[6]，即T＝25 ℃，Cf＝1500 mg/L，Rec＝15%，Pf＝1.034 MPa，相应的标态产水量Qpr＝2.176 m3/h.

为分析给水温度T、回收率Rec、给水压力Pf、给水盐浓度 Cf四项运行条件分别对标准化指标的影响，采用正交实验分析方法.这里选择 T，Rec，Pf，Cf为四因素，每个因素取三个水平，按照 L9(34)正交表进行实验.膜的实测产水量偏差比、模型计算出的标准化产水量偏差比，以及标准化产水量偏差比的因素水平均值K与极差R值示于表1，标准化产水量偏差比的方差分析结果见表2.

表1 四因素三水平正交实验实测结果与标准化结果

表2 方差分析表

由表 1可知：系统实测产水量偏差比EQp的波动幅度在-45.63%～65.30%之间，而标准化产水量偏差比EQpn的波动幅度降至-0.57%～0.91%.可见，膜元件即使未受污染，仅因运行条件的变化就可使膜元件的实测产水量产生很大波动；采用标准化处理后的标准化产水量偏差比的波动幅度则大大降低，其最大波动幅度降低了 98.66%，这说明反渗透膜元件标准化产水量模型在实际工程应用中，为准确判断膜污染提供了巨大帮助.但标准化产水量的偏差比的波动幅度尚偏大，即计算模型存在一定误差.

从表 1还可知，四因素均使标准化产水量产生一定偏差，且其相关性为给水盐浓度的极差＞温度的极差＞回收率的极差＞给水压力的极差.由此可知，给水盐浓度是影响模型产生偏差的关键，远大于其它因素的影响，而给水压力影响最小.由表 2的方差分析表明，给水压力对模型计算结果影响不显著，温度和回收率的改变均对模型计算结果产生显著影响，而给水盐浓度产生的影响高度显著，与表1直观分析的结果一致.换言之，标准化产水量模型中给水盐浓度校正系数ConF对Cf的修正效果最不理想，要进一步加以改进.

3 标准化模型的优化与检验

为减少给水盐浓度 Cf对模型计算结果的影响，引入修正系数α，即以Con F′= α× ConF 取代原模型中的ConF来建立优化模型，且α应为Cf的函数.为求出模型计算结果为理想状况下的α与 Cf的关系，设计如下实验：恒定 T＝25 ℃、Rec＝15%为标准条件，每次实验均改变 Cf，Cf的取值以标态条件下的给水盐浓度为中间值，取值范围在 800～2600 mg/L之间，每次实验 Cf变化 100 mg/L，即做 19个水平的实验.通过调节对模型计算结果影响最小的参数，即给水压力 Pf，以维持膜的实测产水量为标态产水量2.176 m3/h.

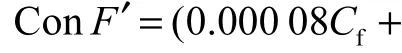
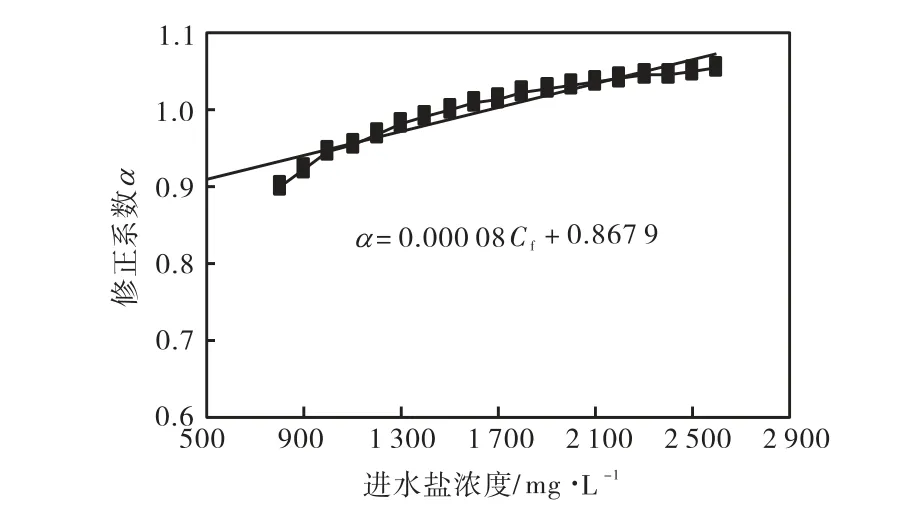
图1 进水盐浓度Cf与α 值的关系曲线

采用上述所示的正交实验，检验以 ConF′代替原模型中ConF后的优化模型计算结果的准确性.检验结果如图 2所示，其中EQpc为优化后模型的标准化产水量偏差比.由图2可以看出，EQpc较原模型计算出的EQpn准确性显著提高.优化后模型产水量偏差比的波动范围在-0.09%～0.14%之间，最大波动幅度比优化前的-0.57%～0.91%降低了84.46%，优化效果十分明显.

图2 优化前后标准化产水量的偏差比

4 结 论

(1)在实验条件下，膜元件运行参数的改变导致反渗透膜实测产水量偏差比的波动范围为-45.63%～65.30%.利用标准化模型计算出的标准化产水量偏差比的波动范围降至-0.57%～0.91%；

(2)给水盐浓度是使标准化产水量模型计算结果产生偏差的最大影响因素，温度、回收率次之，给水压力影响最小；

［1］杨 昆，郭 嘉，王宇彤. 反渗透系统的性能变化分析及量化评价方法[J]. 膜科学与技术，2005，25(5)：54-58.

［2］侯 钰，桑军强，李本高. 反渗透膜污染成因与防治[J]. 工业用水与废水，2008，1(39)：23-26.

［3］罗 浩，江 海，靖大为. 反渗透系统中产水通量的温度特性分析[J]. 天津城市建设学院学报，2006，12(4)：270-272.

［4］MEHDIZADEH H，MOLAIEE-NEJAD Kh，CHONG Y C. Modeling of mass transport of aqueous solutions of multi-solute organics through reverse osmosis membranes in case of solute-membrane affinity：Part 1.Model development and simulation [J]. Journal of Membrane Science，2005，267(1/2)：27-40.

［5］SONG L F，Gurdev Singh. Influence of various monovalent cations and calcium ion on the colloidal fouling potential [J]. Journal of Colloid and Interface Science，2005，289(2)：479-487.

［6］时 均，袁 权， 堦高从 . 膜技术手册[M]. 北京：化学工业出版社，2001.