并联混合有源电力滤波器的参数设计及仿真

纪哲夫

（深圳供电局,广东深圳 518000）

0 引 言

随着工业应用中电力电子设备和家庭负载的不断增多,电网尤其是配变低压侧的谐波成分非常多,严重影响了供电系统的安全、可靠运行。因此电力系统谐波作为衡量电能质量的一项重要指标,对电网质量的研究有着十分重要的意义,引起了各国学者的广泛关注。

电网的谐波治理通常可分为“无源滤波”及“有源滤波”两种。“无源滤波”结构简单、设备投资少、运行费用低且维护方便,但存在一些无法根治的缺点,如:只能滤除特定次谐波,电网参数变化和电网背景谐波电压过大都将导致系统发生串并联谐振,放大谐波电流而烧毁滤波装置等。而“有源滤波”则能对变化的各次谐波和无功进行动态跟踪补偿,同时补偿特性受电网阻抗和频率变化的影响小,还能抑制闪变,改善三相系统的电压对称性,阻尼电压谐波放大等,从而增强了电力系统运行的稳定性。因此自有源滤波器思想提出以来,就被予以了高度的重视,出现了多种应用于不同情况的拓扑结构和检测、控制算法[1-6]。但单一的有源滤波器(APF)成本较高,功率损耗较大,容易受到系统电压等级以及容量的限制,想在电力系统中完全取代PPF还不太现实。将APF和PPF结合在一起构成混合型电力滤波器(HAPF),一方面克服了单独使用APF和PPF的不足;另一方面可以有效降低成本和容量,具有良好的性价比,代表着目前有源滤波技术的一种发展趋势。混合有源滤波器大致可分为串联混合有源滤波器和并联混合有源滤波器。前者主要用来滤除电网的谐波电压,而且需要通过耦合变压器串联在电网中,维护不易;正常工作时,负载的基波电流全都流过变压器,造成装置容量较小,限制了其工程实用性,现已逐渐被并联型混合有源滤波器所取代。故本文主要针对并联型混合滤波器的结构、滤波特性和控制策略进行介绍,在此基础上提出一些参数选择方法并用SIMULINK建立仿真模型对所选参数和控制策略的有效性进行验证。

1 并联混合有源电力滤波器拓扑结构

随着混合有源电力滤波器研究的深入,最早提出的一些拓扑原型都有了一定程度的变化,以克服某些方面的不足,获得更好的滤波性能。本文研究的并联混合有源电力滤波器的结构如图1所示,这是一种新型的拓扑结构,它将有源滤波器与无源滤波器通过耦合变压器串联后再并联接入电源和非线性负载之间,以阻止谐波电流流入电网中。电流互感器和数字控制器实时采样电流后,进行谐波分析计算并产生电压型PWM逆变器的开关信号,控制逆变器产生与检测电流中谐波分量成比例的电压,再通过耦合变压器、无源滤波器和电网阻抗产生与谐波电流大小相等、相位相差180°的补偿电流注入电网,以达到补偿谐波、净化电网的目的。

拓扑中的无源滤波器一般由多个单调谐LC滤波器并联而成,用来滤除电网中的主要次谐波和补偿无功。有源滤波器仅对占少部分的其他次谐波进行动态补偿,主要起抑制无源滤波器和电网阻抗、负载阻抗之间的串并联谐振,改善总体滤波效果的作用,从而减小了有源滤波器的容量,简化了其结构设计。另外,无源滤波器对基频呈高阻抗,使大部分基波电压降在无源两端,有源滤波器的功率器件只承受很低的电压,这减小了有源部分的耐压要求。因此,这种结构方式更适合高压、大功率的应用场合;对低压,小功率的电力系统进行滤波时,可去掉耦合变压器,同样可达到理想的滤波效果,还进一步降低了成本[7]。

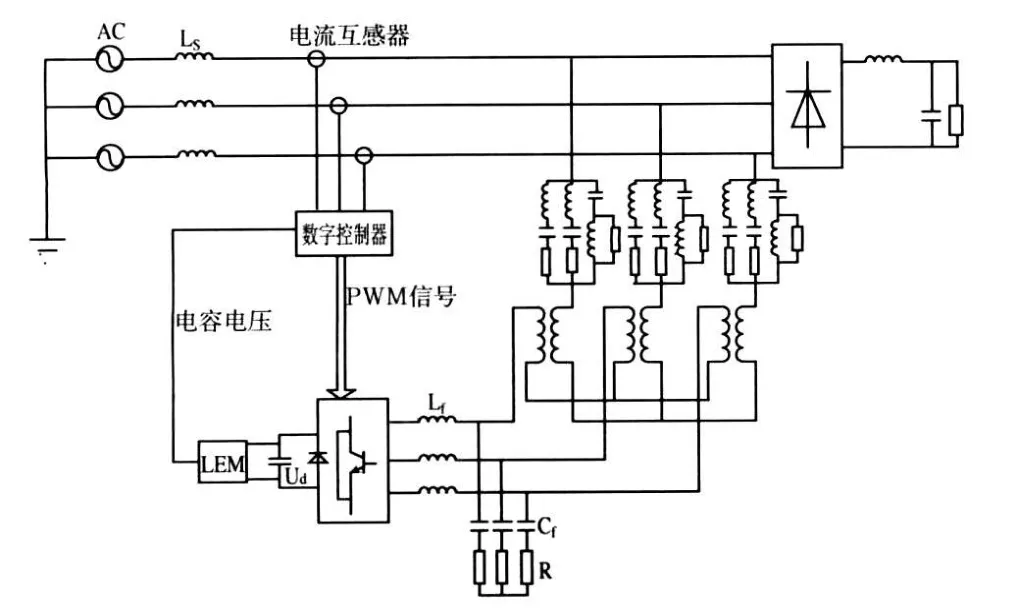
图1 并联混合有源电力滤波器结构

2 控制策略选择

通过电能质量动态监测装置的实地测量可以发现,电网中电压波形一般畸变较小,满足国家相关要求;而电流波形却畸变较大,严重影响电力系统的安全稳定运行[8]。因此,大部分有源滤波实际应用中都是对电流谐波进行补偿的。文中介绍的并联混合有源滤波器通过采用合适的逆变器控制策略,能够很好地达到这个目的。考虑到滤波的总体性能和系统的稳定性,整个控制策略可分为2个部分,下面分别介绍。因为耦合变压器主要起放大PWM逆变器的输出和绝缘的作用,并不影响电路结构。为了简化分析过程,这里假设变压器的变比为1:1;且有源电力滤波器为理想受控源,不考虑数字控制器和开关器件的延时。

2.1 抑制负载谐波电流的控制策略

抑制谐波电流的控制策略一般有3种:

(1)检测滤波器支路电流iCh,控制有源滤波器输出电压(UC=KiCh);

(2)检测负载谐波电流iLh,控制有源滤波器输出电压(UC=KiLh);

(3)检测电网谐波电流iSh,控制有源滤波器输出电压(UC=KiSh)。

策略(1)等效于通过控制有源电力滤波器对谐波呈现为负阻抗特性,来减小滤波器支路的等效谐波阻抗,而电网支路的等效谐波阻抗不变;策略(2)等效于加大电网支路的谐波阻抗,同时减小滤波器支路的谐波阻抗。虽然这两种方法在一些理想情况下可以得到很好的滤波效果,但它们都无法从根本上抑制无源滤波器和电网阻抗发生串并联谐振时对谐波电压和谐波电流的放大[9],因此本文采用控制策略(3)。

假设有源滤波器的输出为受控电压源UC,谐波源看作电流源iLh。其中ZS为电源阻抗,ZF为LC滤波器的总阻抗。则并联有源混合电力滤波器的单相电气模型如图2所示。当仅考虑对负载谐波电流iLh进行补偿,且仅考虑补偿谐波电流时,单相电气模型可简化为图3所示。

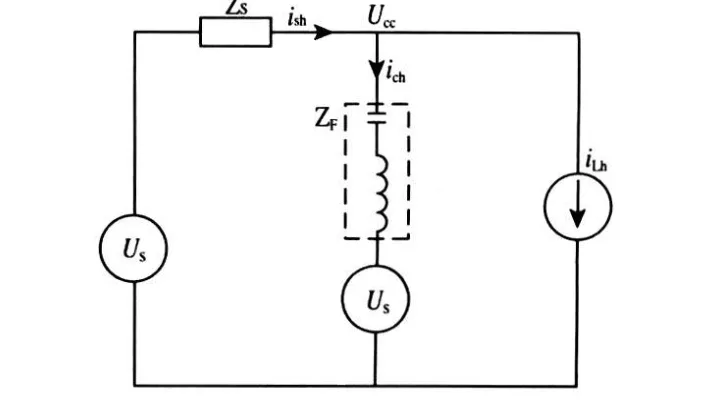
图2 并联混合有源滤波器单相电气模型

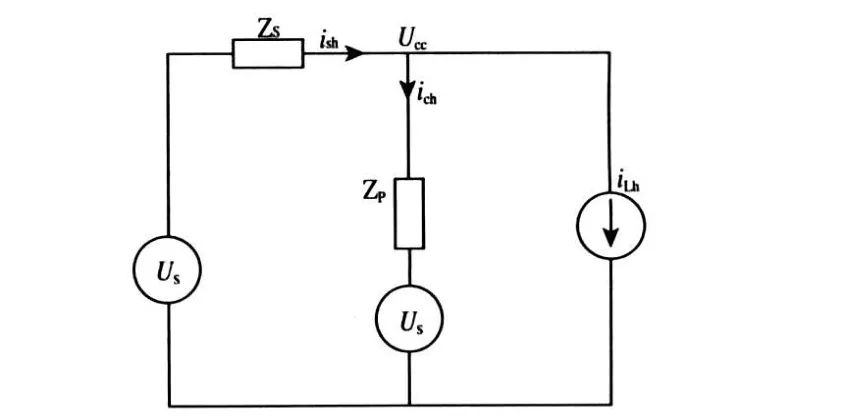
图3 仅考虑补偿谐波电流时的单相电气模型

若控制有源滤波器输出电压UC=KiSh。则由基尔霍夫电压和电流定律可得:

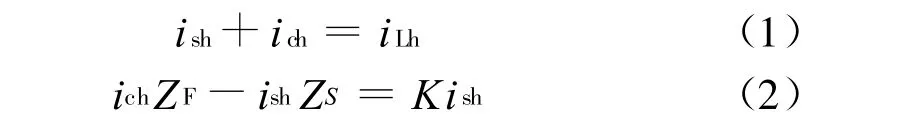
由式(1)和(2)可以得到策略(3)的控制模型和等效电路图,分别如图4、图5所示。

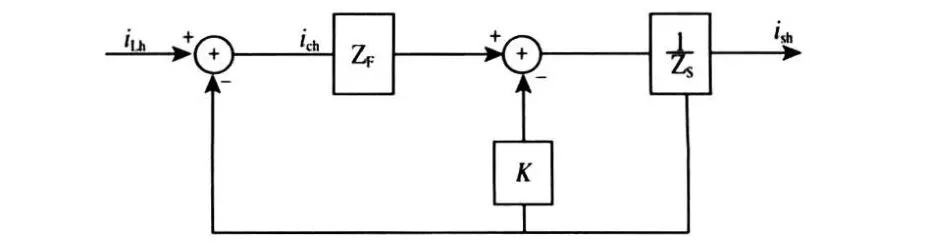
图4 策略3的控制模型

图5 并联混合有源滤波器的单相等效电路图

由图5所示可得iSh的表达式如下:

由式(3)可以看出,策略(3)等效于在电网中串联了一个等效电阻K,增大了电网谐波阻抗,而滤波器支路谐波阻抗不变,从而削弱了电网支路的分流能力,使谐波电流更多的流入滤波器支路,达到滤除谐波的目的。K值越大,滤波效果越好;理论上当K无穷大时,电网电流中将不含谐波;另外,K还能阻尼ZF和ZS发生串并联谐振,抑制电网参数变化、无源滤波器失谐等对滤波效果产生的不良影响[10]。因此,策略(3)是一种理想的控制方法。

2.2 直流侧电容电压稳定的控制策略

并联混合有源电力滤波器实质上相当于补偿电流发生器,为了保证其有良好的跟随性能,必须将有源逆变器直流侧电容电压控制在一个稳定的范围之内。获得稳定直流电压的常用方法有两种:一种是通过调压器和整流电路为直流电容提供一个单独的直流电源,这种方法虽然能够达到目的,但需要另外设计一套电路,增加了整个系统的复杂程度以及成本和损耗。另外一种方法为利用变流器本身来完成能量转换,从交流侧吸收能量给直流电容充电,简单易实现。本文即采用此方法,其原理是:实时检测滤波器支路的基波电流,控制有源电力滤波器产生与基波电流方向相同或相反的基波电压,来实现主动地控制有源电力滤波器从电网吸或向电网释放有功功率。有源电力滤波器产生的基波电压的大小通过直流侧电压的实际值偏离设定值的误差大小来决定,其控制原理图如图6所示。

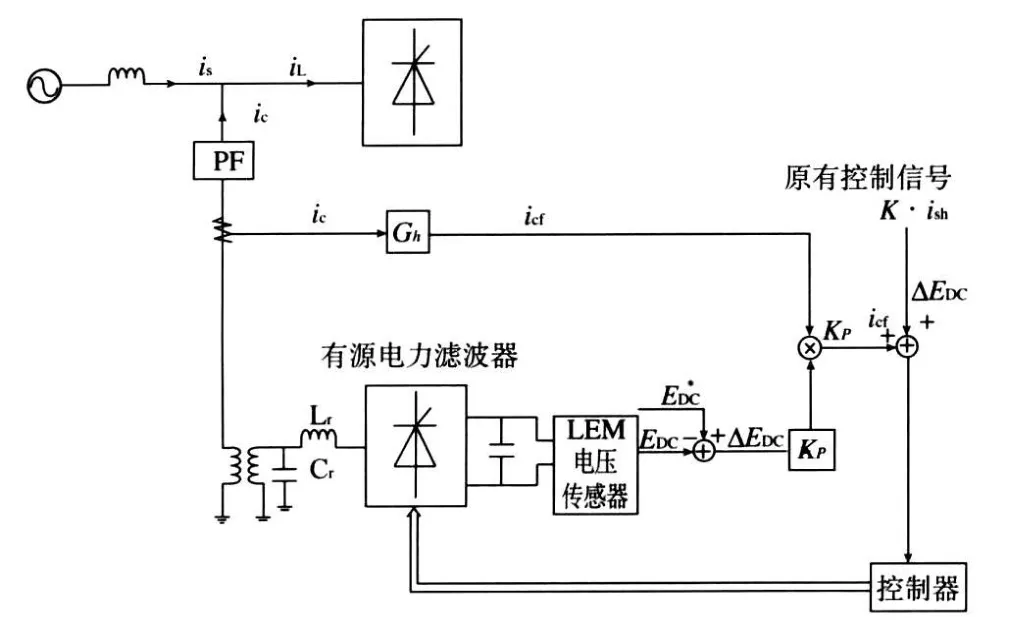
图6 直流侧电压控制原理图

图6中,Gh为基波电流检测环节,EDC*为给定的直流侧电容电压,EDC为实际的电容电压,它们之间的差值△EDC扩大Kp倍后,与滤波器支路的基波电流iCF相乘,作为控制直流侧电容电压稳定的控制信号。

3 参数设计

并联混合有源电力滤波器是一个复杂的电力电子设备,各部分的参数设计不仅关系着自身工作性能的好坏,还对其他组成部分的性能和总的滤波效果有着重要的影响,因此需要综合多方面进行考虑。根据系统的结构,其参数设计大致可分为无源滤波器的参数设计,开关纹波滤波器的参数设计、直流侧电容的参数设计以及耦合变压器的参数设计四个部分,下面分别介绍。

3.1 无源滤波器的参数设计

无源电力滤波器的设计应遵循以下三条原则:

(1)对电网主要谐波呈现为低阻抗;

(2)对基波呈现为高阻抗;

(3)在满足前两条原则的前提下,尽可能降低成本。

单调谐无源滤波器是利用电感、电容的串联谐振原理构成的。滤波器对n次谐波的阻抗为

其中,w1为基波角频率,滤波器的谐振频率为

另外,单调谐滤波器品质因数的定义为

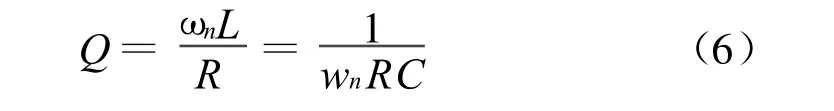
单调谐无源滤波器的品质因数是一个非常重要的参数。滤波器对于调谐频率的谐波阻抗与其品质因数Q成反比,即Q越大,阻抗越小,其阻抗的频率响应曲线越尖锐,频率选择性越好。但是,滤波器对于参数的变化会越敏感,一旦失谐,其性能将会变化很大,而且一旦无源滤波器和电网发生串、并联谐振,谐波放大的程度也越大。因此,滤波器的品质因数不能取得太大,也不能取得太小,工程上一般取10～40。

本系统是利用逆变器自身来完成能量转换的,从交流侧获得能量转换到直流侧,因此必须使得流过无源滤波器的基波电流流向逆变器直流侧提供的有功功率大于需要补偿的谐波容量,这样才能维持直流侧电容电压稳定,而且基波电流越大直流侧电压越稳定,动态响应越快,但是由于无源支路电阻的存在,损耗也越大。这就要求在保证谐振频率的基础上,合适地选择L、C、R的值,使流过无源的基波电流满足要求。

因为系统中采用的是二极管不可控整流负载,产生的主要次谐波为 5、7、11、13、17、19 次谐波 。故无源滤波器采用5次、7次单调谐滤波器和高通滤波器并联而成。加高通滤波器主要是因为5、7次无源滤波器对高次谐波的阻抗较大,滤波效果受到影响。

综合考虑以上要求,文章 L5、C5、R5和 Q分别取6.77 mH 、60 μ F 、0.08 Ω、10;L7 、C7 、R7和 Q 分别取 4.144 mH 、50 μ F 、0.071 Ω、10;高通滤波器 Lh、Ch和 Rh分别取 2 mH 、80 μ F 、1 Ω。

3.2 开关纹波滤波器的参数设计

逆变器输出电压中除了含有所需的补偿电压外,还含有逆变器开关频率和开关频率整数倍附近的高频谐波。如果将这些开关纹波也注入电路中,显然会给电网带来新的高频谐波污染,严重时还可能导致有源滤波系统本身因过流、过压而不能正常工作,甚至毁坏。因此必须用滤波器将逆变器工作引起的开关纹波滤除。在开关纹波滤波器的参数设计中,为了保证开关纹波衰减,一般截止频率选为开关频率的1/5至1/10,而且要大于有源滤波器的最大补偿谐波频率。在本系统中PWM载波频率选为12800 Hz,最大补偿谐波频率为2500 Hz,综合考虑选择开关纹波滤波器截止频率为4500 Hz。根据截止频率还不能确定 Lr、Cr的大小,还要考虑 Lr、Cr的分压,这决定了逆变器的带负载能力。因为Cr与Zs+Zf(无源滤波器阻抗)并联,则需要XCr远大于Zs+Zf,而Lr与 Zs+Zf串联 ,则 需要 XLr远小于 Zs+Zf。为使Lr、Cr谐振频率附近的谐波不被开关纹波滤波器过度放大的现象,需要在滤波电容支路串联一个电阻,抑制谐振的产生。

综合以上要求,开关纹波滤波器L、C、R参数选择为 0.4 mH 、5 μ F 、1 Ω。

3.3 直流侧电容的参数选择

为了保证并联混合有源电力滤波器输出预定的电压,电压型逆变器的直流侧电容电压必须保持恒定。为了减小直流侧电容电压的波动,直流侧电容必须有一定的容量要求。当直流侧电压一定时,电容值越大,越有利于电容电压的稳定。但还需考虑成本、体积等问题,进行合理选择。

工程实践中确定电容量的主要依据是限制逆变器工作在最低输出频率和额定输出电流时直流电压的低频脉动率。所需滤波电容量可按工程经验公式计算:

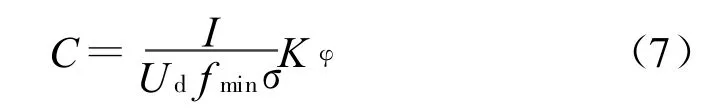
式中,I为逆变器的额定输出电流均方根值;Ud为直流电压平均值;fmin为逆变器的最低输出频率;σ为允许的直流电压频率低峰值纹波因数;Kφ为负载位移因数角φ有关的系数。

从有源滤波器的原理可知,直流侧电容电压越大,则逆变器输出谐波电压幅值越大,补偿效果越好。但是在给直流电容充电时,逆变器实际工作在整流状态,还应考虑动态响应速度和滤波器支路基波电流这两个因数。可见直流侧电容电压选择有着严格限制,不能过高。通过研究发现,电容电压选定在1000 V以下是合适的,这里选择1000 V作为直流侧电容电压,由式(7)得出电容值选择10000 μ F较为合适。

3.4 耦合变压器的参数选择

在耦合变压器容量足够且磁芯未饱和时,变压器变比是影响滤波效果最重要的参数。一方面由于等效阻抗K的大小是由直流侧电容电压、逆变器的放大倍数和变压器变比决定的。对特定次谐波,无源滤波器阻抗较小,K值影响不大;但是对非特定次谐波,无源阻抗较大,要改善滤波效果必须增大K值,而当直流侧电容电压值确定时,逆变器对K值的增大作用有限,因此变压器的变比对滤波效果至关重要。理论上变压器变比越大滤波效果越好,但是K处于闭环控制系统之内,取值太大容易使系统不稳定,基波附近的谐波(25 Hz、75 Hz和100 Hz)将被放大的更多,反而使滤波效果变差[10]。另一方面,变压器的变比也和有源部分的容量密切相关。混合并联有源滤波器利用无源部分承受大部分基波电压来降低有源部分的耐压等级。但是无源滤波器对基波总有一个阻抗,不可能无穷大。在低压时,由于产生的基波电流很小,对容量影响不大;但是在高压时,将产生一个不小的电流,通过变压器耦合后,这个基波电流放大数倍(和变压器变比有关)后,流入逆变器,使有源滤波器的容量增大。因此需要综合考虑这两方面,合理选择变压器变比。

因为变压器流过的电流主要用于保持逆变器直流侧电容电压恒定的基波电流和各次谐波电流,所以变压器的容量可用下面公式进行简单估算。

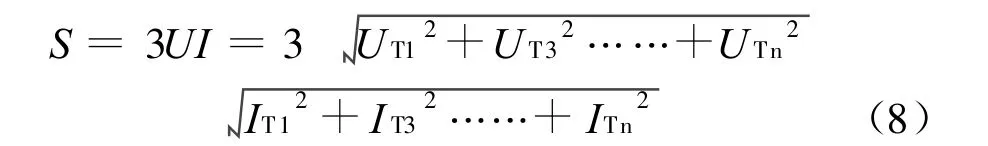
式中,UT1和 ITI为分别流过变压器的基波电压和电流的有效值;UTn和ITn为二极管不可控整流负载产生的n次谐波电压和谐波电流的有效值。

此外,耦合变压器的漏感设计得越小越好。变压器的漏感越小,损耗越小,变压器的频率特性也越好,同时,也有利于有源滤波器容量要求的降低。

综合以上所述,变压器变比为1200:4800,容量取为100 Mvar。

4 仿真结果

根据前面所述的控制策略和参数选择原则,用SIMULINK搭建仿真模型。图7是主电路的仿真框图;图8是控制部分的仿真框图。

图7 主电路仿真框图

图9和图10分别是仅投无源滤波器和投入混合滤波器两种情况下的电网电流波形和频谱分析图。

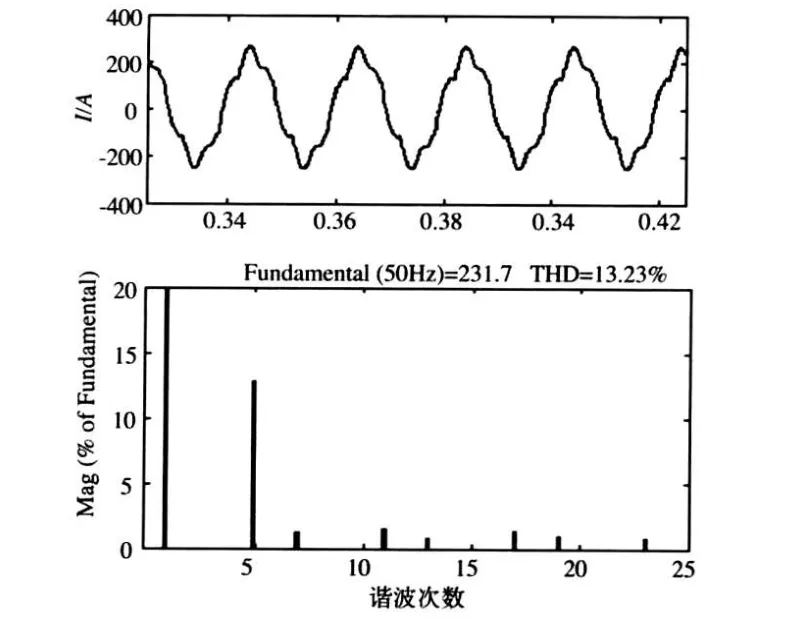
图9 仅投无源滤波器时的电网电流波形和频谱图

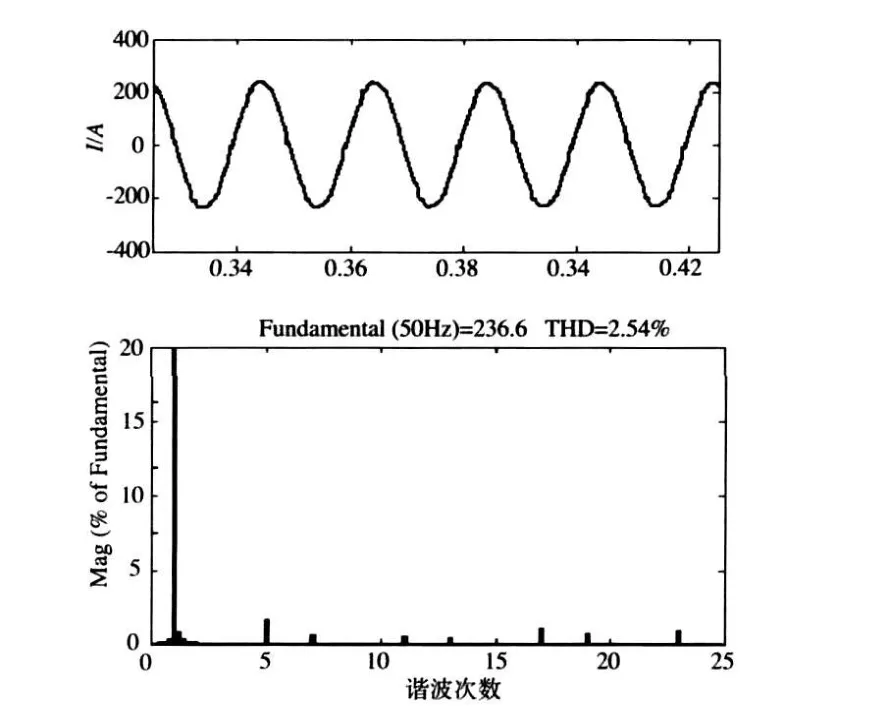
图10 投混合滤波器时的电网电流波形和频谱图

5 结 论

从仿真结果可以看出,当仅投入无源滤波器时,电网谐波电流的THD从40%降为14%,投入有源滤波器后,THD降为3%左右,这说明了有源滤波器确实能改善整体滤波效果,同时也证明了所采用的控制策略和所选参数的有效性。文中所设计的混合有源电力滤波器结构较为简单,控制方法易于实现,非常适合应用于工程实践中。

[1]Fujitia H Akagi H.The Unified Power Quality Conditioner:The Intergration of Series and Shunt Filter[C].Proceedings of PESC'1996:494-501.

[2]Gyugyi L,Strycula E C.Active AC Power Filters[C].Proceedings of IEEE/IAS Annual Meeting,1976:529-535.

[3]Hirofumi Akagi,Edson Hirokazu Watanabe,Mauricio Aredes.Instantaneous Power Theory and Applications to Power Conditioning[M].IEEE Press.

[4]Take M,Ikcda K,Teramoto A,etal.Harmonic Current and Reactive Power Compensation with an Active Filter[C].IEEEE-PESC,1998,1174-1179.

[5]Peng F Z,Akagi H,Nabae A.A New Approach to Harmonic Compensation in Power System[C].IEEE IAS Conference Record,1988:874-880.

[6]Fujita H,Akagi H.A Practical Approach to Harmonic Compensation in Power System-Series Connection of Passive and Active Filters[C].IEEE IAS Annual Meeting Conference Record,1990:1107-1112.

[7]武 健,何 娜,徐殿国.无变压器型并联混合有源滤波器设计及应用[J].中国电机工程学报,2008,28(12):88-94.

[8]谢明磊,丘东元,张 波.分布式多路动态谐波检测装置的原理和实现[J].电气应用,2008,12:81-86.

[9]王莉娜.厂矿企业配电网谐波治理控制策略和工程应用研究[D].长沙:中南大学信息科学与工程学院,2003.

[10]贾 煜.新型混合型大功率有源电力滤波器控制方法及装置的研究[D].长沙:湖南大学,2007.