世界最早的天文观象台
——陶寺观象台及其可能的观测年代
2010-10-27李勇
李 勇
(中国科学院 国家天文台,北京 100012)
世界最早的天文观象台
——陶寺观象台及其可能的观测年代
李 勇
(中国科学院 国家天文台,北京 100012)
2005年在山西襄汾陶寺镇发现了世界上最早的天文观象台遗址——陶寺观象台,它呈扇形结构,主要由 1个观测点和东侧的 12条观测缝组成。为考察其作为古观象台的必要条件,借鉴现代实测方式,采用计算机系统对其在BC 3000—BC 1000年间作日切山顶的模拟观测,结论是该观象台可能的观测年代应早于BC 1500年,且最佳观测年份为BC 1956年,12条缝能观测 21次,平均每缝的观测误差为 0°.11,最大误差 0°.7。观测日期与邻近节气的平均误差为 4.5日。指出:观象台的观象目的可能是对陶寺文化中特定的时节 (也许是处于萌芽状的节气)进行观测,亦或用以提供进行祭祀等重要活动的时刻。但由于该遗址的地表部分不存,已知信息有限,故难作准确推论。
考古天文学 陶寺 观象台遗址 观测年代
0 引 言
2005年,考古工作者在中国山西省发现全世界最古老的天文观象台遗址——陶寺观象台。据初步认定,该观象台形成于公元前 2100年的原始社会末期,它比中美洲的玛雅天文台遗址还早千年,比英国索尔兹伯里 (Salisbury)平原上的史前巨石阵观测台还要早近 500年,这可能是世界上最早的天文观象台。
经中国社会科学院考古研究所组织,笔者于 2005年 10月 22日到陶寺遗址现场考察,24日参加了在中国社会科学院召开的“陶寺城址大型特殊建筑功能及科学意义论证会”。会前考古队准备了相关材料[1—2],包括 2年的模拟实测数据和先期的天文年代研究[3—4]。会上 10余位天文学者畅所欲言,席泽宗院士指出:“以往我们的天文考古研究主要是研究与天文有关的出土文物,缺乏西方那样对史前天文遗址的研究。陶寺天文观测遗迹的发现,是中国考古天文学的真正开端”[5]。
古有“尧都平阳”及陶唐氏之说,今在山西临汾一带,更有研究者认定尧都就位于今天的陶寺遗址,故对陶寺城址大型特殊建筑的天文功能作深入研究很有必要。笔者“基本认同 IIFJT1的功能为兼观象授时与祭祀为一体的建筑,它极可能是用于观测某天体(诸如太阳)所处特定位置 (方位)时进行祭祀活动的场所,但其具体的天文功能尚需进一步详加论证。”同时还提出:“就现有工作看,有待补充一个更为详细而专业的天文论证报告,以保证 4000年前的陶寺地区的确可以实现所设定的天象观测。现代实测固然重要,它能积累数据、获取精度,但无疑古代的模拟观测更为重要。可喜的是,现代的计算机完全能胜任并完成这一复杂工作。尽管古今观测必存差异,但当时的观测却更具意义,只有这样才可进一步讨论其观象功能的细节”[5]。2007年《山西襄汾县陶寺中期城址大型建筑 IIFJT1基址 2004~2005年发掘简报》发表[6],相关数据正式出版,笔者的这一计划才得以实施。
观测天象、制定历法是华夏文明诞生的重要标志。考虑到由于该建筑地表部分不存,不确定因素和可供想像的空间都较大,本文仅立足于考察其作为古天文台的必要条件,着力复原古代的观测情况,进而讨论其可能的观测年代。基于这一思路,我们依据精确的观测点及测量缝数据,采用现代的天文历算方法进行回推,考察其可能的观测年代及观测方法。
1 陶寺观象台遗址概况及现代的模拟实测
山西襄汾县陶寺中期城址大型建筑 IIFJT1基址自 2003年即开始作考古发掘[7],现初步认定为 4100年前世界上最早的观象台。陶寺观象台遗址位于山西省临汾市襄汾县陶寺乡东坡沟村。2004—2005年该遗址又进一步发掘[6],该观象台呈半圆形平台,有三个圈层的夯土结构。第一圈的半径大约 18米,第二圈大约有 24米,第三圈大约为 50米。观测中心和 12条由夯土柱构成的观测缝呈扇状辐射排列,观测中心距观测缝的距离约10.5米 ,各缝张角大多在 1°—2°内 (图 1)。
考古专家曾推测,这 10余座夯土柱上面应建石柱,将观测缝留出,石柱高约 5米左右。观测者直立于观测点核心圆上,透过柱与柱之间的缝隙观测正东方向的日切塔儿山山顶时是否在缝中央,并以此来确定当时的节气或历法中某些特定的日子。
经大地测量 ,获得遗址观测点的位置 :北纬 35°52′55″.8及东经 111°29′55″.0。12条观测缝中线的方位角和远处山顶的仰角数据见表 1。
为此,中国社会科学院考古所山西队在 2003年 12月 22日至 2005年 12月 22日间还进行了为期 2年的实地模拟观测,总计 72次,确认通过这 12道狭缝可观测到 20次日出天象。由这些数据可得观测缝的最佳观测日期与节气的平均误差 =4.0日 (表 1)。其观测报告指出[3]:“陶寺观象台总计 12道观测缝,从观测点可以观测到冬至—夏至—冬至一个太阳回归年的 20个时节的缝中线日半出或日切。这 12道缝中 1号缝没有观测日出功能,7号缝居中,为春分、秋分观测缝。7号缝向南间隔 5道缝至冬至日半出,向北间隔 5道缝至夏至日半出。除 2号缝观测冬至、12号缝观测夏至各用一次之外,其余 9道缝皆于上半年和下半年各用一次。”鉴于观测结果中只有少数观测缝与节气有较为明显的对应关系,他们认为:对于陶寺 20个时节中除二分二至以外其余 18个时节的意义,尚需另文讨论。在论证会所提供的材料中也逐一给出了与生产、生活及祭祀活动相关联的初步推测结果。
实际上现代所作的模拟观测并不等同于历史时期的真实观测,而当时的观测对于遗址的观象考证更为重要。下文就是借助现代的计算机技术来实现对古代的模拟观测。

图1 观测点夯土基础和柱缝基础局部图[6]

表1 12条观测缝中线的方位角和远处山顶的仰角数据及现代模拟观测结果
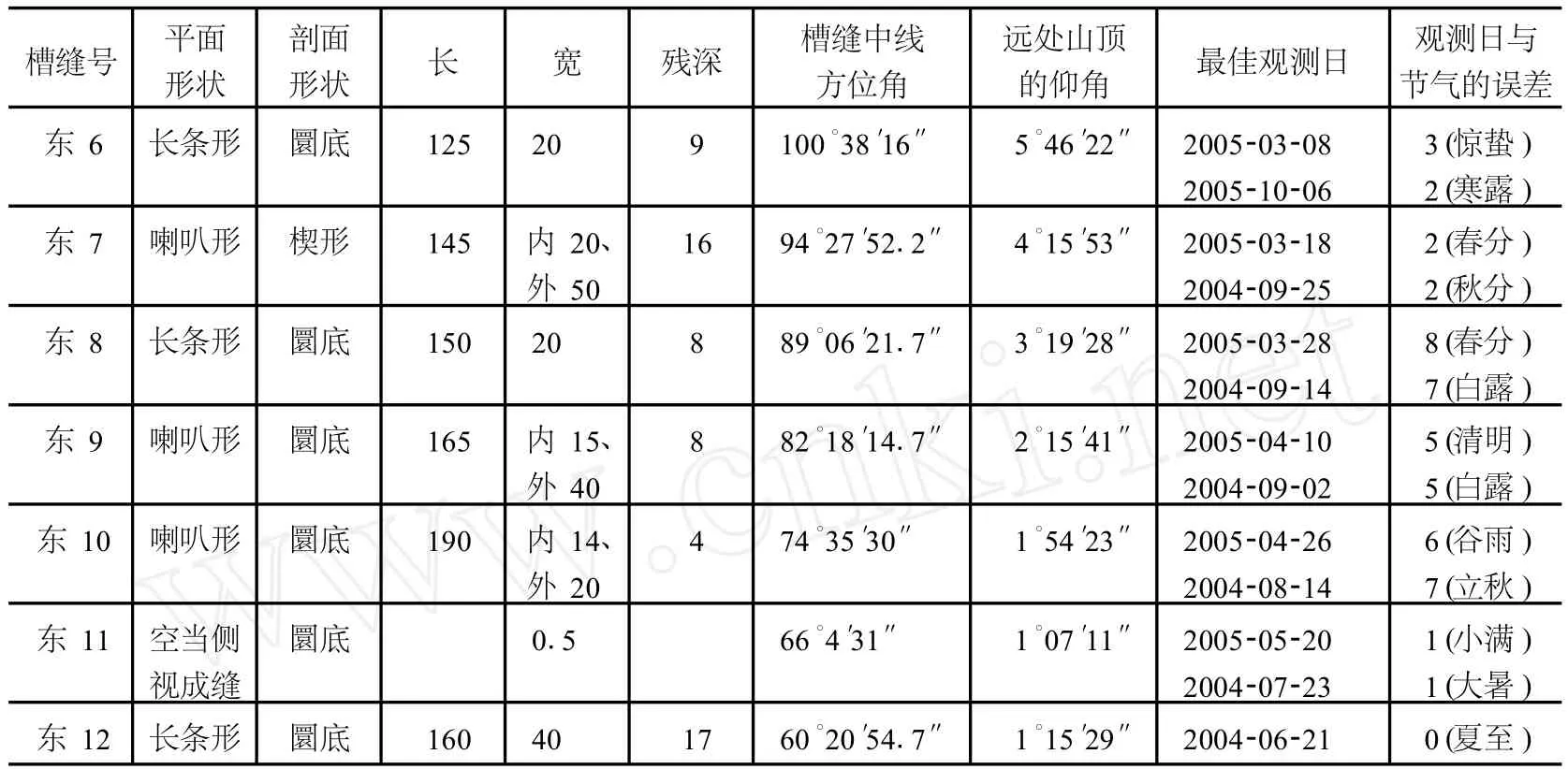
续表1
2 计算机模拟观测
显然,要严格论证该建筑确为古代的天文台遗址还有一定困难。因为它既无保存完整的观象设施,又无可作旁证的文献依据。尽管如此,不可否认,现有的结构已能表明其具有作为古观象台的可能性,对此本文不作深究,而是姑且承认该大型建筑具有天象观测功能,且观测方法如前所述,即采用狭缝观测日切山头。考古队现代的模拟观测亦肯定了这一观测方案的可行性。采用计算机模拟所需要的数据有:观测中心的地理坐标,12条观测缝的方位角及远山的仰角,这些上文已作交待。本文只是根据天象回推方法[8],试图计算出这一观测系统的最佳观测年份,并通过计算机复原当时的观测情况。
要想深入分析陶寺天文台的观象方法,不仅需要对古代的模拟观测,而且还要准确还原古代的观测结果。这就需要采用反演方法,这实际上比现代的模拟观测更为重要。为此笔者专门设计了计算软件,它可同时解算由 12条观测缝所组成的观测系统,从而精确求解,包括其可能的观测年代。计算采用长周期的 DE 406历表,其适用的年代区间为-3000年至 +3000年,而地球自转长期变化数值ΔT则取自 Stephenson等 1995年的研究结果[9]。
集成的软件只涉及到太阳在地平坐标系中视位置的计算,至于太阳视位置的计算方法可参阅天文书刊,本文只是给出如何利用它来求解陶寺观测系统的最佳年代,其具体的设计如下:
为便于讨论,首先定义角度误差 Def,它指计算所得的太阳位置与给定的观测缝的方位角(Az)及相应山顶仰角 (El)的误差,具体可表示为方位角误差绝对值与地平高度误差绝对值之和,即:Def=abs(A-Az)+abs(E-El),其中:A和 E分别为方位角与地平高度的计算值,Az和 El的数据列于表 1。
于是,对于有 N条观测缝 (N=12)的日出观测系统,可建立起误差和 Sum的观测 (误差 )方程:

考虑到太阳的视半径有 16′(0°.27),我们设定可允许的最大角度误差为 0°.8,并筛选出Def<0°.8的结果。计算时需输入的参数有:12个槽缝的方位角和仰角;观测中心的地理经纬度;计算的始末年;计算步长;最大角度误差等。将以上数据代入程序,在规定的误差 (Def<0°.8)范围内,求出同年内满足最多的观测缝能够观测到日切山头、且累计的角度误差 Sum最小的观测方案(日期序列),即为最佳结果。
随后,我们取求解的年代范围为 BC 3000—BC 1000年,给定这一区间,以便获取陶寺天文观象台的最佳观测年代。计算时首先取步长 =0.001日 (即 1.44min)作粗算,求出最佳的 3个观测年份为 BC 1585年、BC 1626年和 BC 1956年。
具体而言,从 BC 3000—BC 1000年,每隔 1.44min计算一次太阳在地平坐标系中的位置,并求解 Def值。对某缝而言,当 Def<0°.8时,观测结果被记录下来,包括日期、时刻、方位角 (A)和仰角 (E)。随着一次次的叠代,取 Def值最小的那一次为该缝相对于某年的最佳结果,当该年所有缝计算完毕后,即得出该年合计可观测到的缝数 (须满足 Def<0°.8),以及误差和 Sum值。经过比较每一年的结果,最终可得出在给定年代区间内的最佳的结果 (即具有最多观测缝和最小 Sum值的年份),而所记录下的与各缝及最小 Def值相应的观测时刻,即为最佳时刻。
对于所得出的数个最佳观测年份。然后再以步长 =0.0001日 (约 8.6sec)精算,这样的处理可节约大量计算时间,得出累计角度误差 Sum最小的年份是 BC 1956年,这就是在给定年代区间内的最佳观测年份,其累计角度误差为 2°.30,而平均每条缝的观测误差为 0°.11。详细计算结果列于表 2。
作为比照,我们亦取 AD 1900—AD 2010时段进行考察,表 2中也列出了相应的计算结果。求得现代最佳的 3个观测年份为 2009年、1976年和 1927年。最后又确定 AD 2009年为最佳观测年份,其累计角度误差为 2°.08,平均每条缝的观测误差为 0°.11。

表2 采用计算机对 AD 1900—AD 2010及 BC 3000—BC 1000年代区间作模拟观测分别得出 3组最佳结果

续表2

续表2

续表2
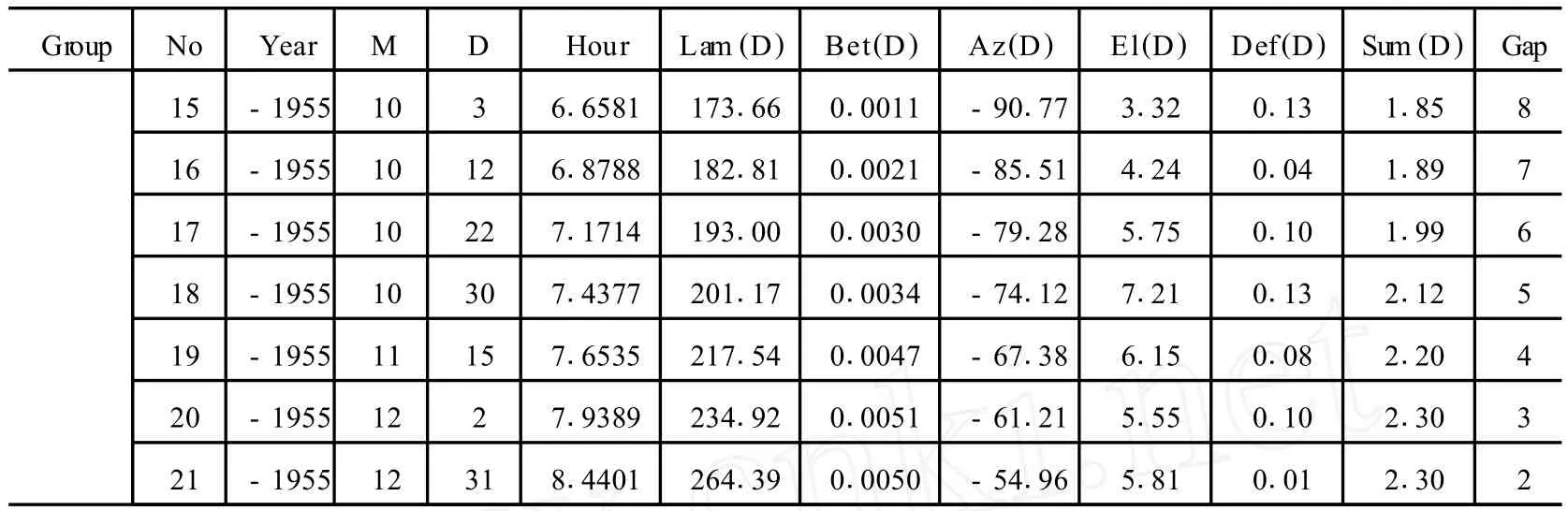
续表2
计算结果表明古代的观测好于现代。因为在一个回归年内,12条缝古代最多可观测21次,仅第 1条缝不能观测,且第 12条缝的误差最大约 0°.7左右。而现代则最多能观测到 19次,且第 1和第 12条缝不能被观测到,最大误差是第 2条缝,约 0°.5。
总之,在求得的古代结果中,由于三个最佳观测年代均早于 BC 1500年,故本文初步判断该观象台可能的观测年代应早于 BC 1500年,且最优结果为公元前 1956年,其相应的观测日期列于表 2。
3 几点讨论
(1)节气问题
就狭缝 1年内所能观测到的节气而言,误差在 1日内的较少。据表 2的计算机模拟,现代有在第 2缝观测到的冬至,误差为 0日,以及在第 11条缝观测的小满和大暑,误差 1日。现代的实测与此同,但另增加了一条夏至的误差为 0日 (表 1)。古代则仅有在第 12条缝观测到的夏至,误差为 0日。由此,观测最为准确的节气是当数冬至 (现代)和夏至(古代),但两者的观测误差却较大,不低于 0°.5,远高于其他观测缝的角度误差值。且在本文设定的误差范围 (Def<0°.8)内,现代能观测到冬至却见不到夏至,古代则正好相反。同时,根据表 2提供的观测日期和太阳黄经值还可判断日期与节气的关系。若以 2009年为例,则可得出观测日与节气的平均误差为 4.1日,而考古队 2年的实测所得平均误差为4.0日 (表 1);若以 BC 1956年为例,则相应的平均误差是 4.5日。
这一结果表明:该遗址所构成的观测系统似乎并不主要用于观测节气,因为精度问题,从而与当初节气观测说的猜测难以吻合。否则,在本文设定的狭缝观测框架下又如何解释?我们以为,4000年前的陶寺先民,可能受到当时种种条件的限制,一方面仰观天文知识不足、天象观测精度低下;另一方面他们对太阳周年运动与人类活动的关系,特别是节气的认识尚处浅显阶段。正如张培瑜先生所说:距今 4000年前的先民不可能有二十四节气的划分,但据《尧典》记载,当时应已知“二分和二至”、“日中”、“日永”、“日短”、“宵中”[5]。此外,也有学者提出尧时历法中一年有 20个节气之说[10]。在此情形下,他们最初观测的可能是陶寺文化中的特定日期,以指示从事某些生产、生活和祭礼活动的时间。而这些日期经过演变,并逐渐固定下来,或许就与后世的节气相关联了。它暗示着先民对节气的认识曾经历了一个漫长的过程,而陶寺观象台的观测正好处于这一萌芽时期。故本文以后世形成的二十四节气为参照基准,得出陶寺观象台观测节气的误差偏大就不足为怪了。或许陶寺观象台就是一个 4000年前萌芽状的节气观测系统。
(2)唯一性问题
如果该建筑真具观象功能,则其用途无非是观测节气以确定历法,所谓观象授时;或演示特定天象,诸如当某类天象出现这一特定的时刻,开始祭祀活动。可能起源甚早的土圭定节气之法应比陶寺观象台测日切山顶之法更为有效、方便。但遗憾的是,遗址的地表部分缺失,所造成的不确定性增加,可供想象的空间很大。我们在承认它是观象台的同时,也得承认与其相应的观测设备、观测方案、观测对象等信息均无存。这一现状导致该建筑物的天象观测的实现方法并不唯一,因为当面对这些观测缝和观测中心时,其地表部分仍可能有所变化。就建筑物自身而言,究竟采用何种观测方式,并不明晰。即便采用狭缝观测,实际的观测缝也完全可能与夯土柱的缝不一致。再者,日切山顶的观测方案也只是一个近乎合理且无法证实的假设。而且,就观测对象而言,太阳虽然会首先被想到,但是否还包括其他天体,诸如行星、恒星、流星、客星、彗星等?另外,就观测目的论,是为制定历法等天文学用途?还是仅充当计时工具,以提供特定的祭祀时刻?还是两者并存?
例如,笔者曾根据残存的 10余根夯土桩及其深度从 1.9m至 5.4m不等这一事实,对采用狭缝观测的方案提过异议,也对“直接望日”观测提出过怀疑[5]。但本文为避免问题的复杂化,求解工作仍基于狭缝的对日观测进行。
考虑到陶寺观象台遗址的现状,以及诸多不确定因素,都给研究工作及问题的最终解决带来了障碍。
(3)求解细节
考虑到太阳视半径、大气折射以及观测误差等原因,本文设定可允许的最大方位角和仰角误差和为 0°.8。这只是用以定义观测缝可见 (或不可见)观测目标的参数。实际上若改变设定,对本文年代的求解影响不大,只是该年份 12缝可观测日出山顶的次数可能有所变化。实际上本文提供的 3解,最大观测误差均出现在第 12缝,即所谓夏至观测缝,它的误差达 0°.7,此外的最大误差仅为 0°.23。试想若严格定义可允许的最大角度误差为 0°.3,则所求最佳结果的年份并不改变,但该年 12缝共可观测 20次,而不是 21次。
若由单缝求解对应的观测年份,理论上是可行的,但实际难以奏效。它的求解与本文提出的多缝求解并无本质差别,不同在于单缝对结果的筛选效率较低,最终将面对众多的可能解而无从选择。本文设计的求解方法正是利用多缝进行联合求解,其奥妙在于可高效筛选或锁定最佳结果,因为它相当于增加了求解的约束条件,从而把不可能变为可能。故利用多缝观测系统进行求解正是这一方法的优势,若用单缝求解则失去了这一优势,除非加入其他较强的限定条件,例如该缝用于观测特定节气、观测时间固定等,但那样进行求解的恐怕就不是陶寺问题了。正是本文提供的方法使陶寺观象台这样的多缝观测系统观测年代的精确求解成为可能。
本文选择观测误差最小的年代以作为陶寺观象台可能的观测年代,并给出了 BC3000—BC 1000年代区间内的 3个最佳结果。如何进一步评价这些结果?后续工作可提供求解结果的逐年误差分布,以便考察每年观测误差的分布情况,同时研究者还可利用它进一步考虑解的合理性等问题,从而对可能的观测年代作出取舍。本文选取误差最小的年代作为可能的观测年代只是其中的方案之一,当然亦可根据某时段的平均误差最小来选取年代。故这个问题尚有进一步讨论的余地。
只有建立了行之有效的求解方法,并获取结果,才能为最终年代的确定提供可能。定量研究和精确求解也体现了史学和考古研究的发展趋势。综上所述,本文所建立的方法有可能经过逐步发展,形成一套普适的方法,用以精确求解柱竿类日出观测系统的观测年代,陶寺观象台的发现为这一方法的建立提供了契机。
(4)初步结论
陶寺天文观象台的发现及功能论证是中国考古天文学领域的一枝奇葩。我们依据现有的遗存情况和假设,仅对通过狭缝作日切山顶观测这一观象功能进行了初步探讨。计算得出该观象台的观测年代应早于 BC 1500年,且最佳观测年份是公元前 1956年。表明这一年份极可能与该观象台的建成或开始观测的年代相关联。由此得出该建筑的主要观象功能可能是对日切山顶天象进行观测,以观测并确定与陶寺文化相关的时节,这些时节可能是陶寺文化特有的,也可能就是处于萌芽时期的二十四节气;或借助对日切山顶天象的观测以确定某些特殊时刻,从事祭祀等重要活动。或许这就是该部分建筑的目的所在,相当于当时通过天象观测加以实现的测时和守时系统。但由于种种不确定性,目前我们据此尚无法构建一个完整的陶寺观象台的观象授时系统,类似于曾探讨过的北斗观象授时系统[11]。
总之,该建筑应基于一定的历法背景,并通过观测天象的位置以考定时节、确定时间。需要强调:相比而言陶寺观象台更适合于古代的观测而不是现代,故作为古代的观象台极有可能!同时,本文也为其可能的观测年代提供了参考基准。
注意到有学者研究了陶寺观象台遗址的天文功能及相应的年代问题[12],但研究者发现用黄赤交角的长期变化反演出的年代 (约 -3500年)与考古学估定的年代 (约 -2100年)存在较大差异,是什么原因导致了这一结果?本文采用的天文方法与其不同,结果(-1955年)亦与其相差较大,但却与考古学结论相近。可见,陶寺观象台及其年代问题值得进一步关注和深入探讨。
致 谢 感谢中国社会科学院考古研究所提供笔者实地考察的机会。感谢该所山西工作队,特别是何驽先生给予的帮助。感谢审稿者的意见,促成本文的进一步充实。
1 何驽.陶寺中期小城内大型建筑 IIFJT1发掘心路历程杂谈[A].新世纪的中国考古学——王仲殊八十华诞纪念文集[C].北京:科学出版社,2005.228
2 中国社会科学院考古研究所山西队,山西省考古研究所,临汾市文物局.2004~2005年山西襄汾陶寺遗址发掘新进展[J].中国社会科学院古代文明研究中心通讯,2005,(10):58—64.
3 中国社会科学院考古研究所山西队.陶寺中期小城大型建筑基址 IIFJT1实地模拟观测报告[J].古代文明研究通讯,2006,(29):3—14.
4 武家璧,何驽.陶寺大型建筑 IIFJT1的天文学年代初探[J].中国社会科学院古代文明研究中心通讯,2005,(8):50—55.
5 江晓原,陈晓中,伊世同,等.山西襄汾陶寺城址天文观测遗迹功能讨论[J].考古,2006,(11):81—94.
6 中国社会科学院考古研究所山西队,山西省考古研究所,临汾市文物局.山西襄汾县陶寺中期城址大型建筑IIFJT1基址 2004~2005年发掘简报[J].考古,2007,(4):3—25.
7 中国社会科学院考古研究所山西队,山西省考古研究所,临汾市文物局.山西襄汾县陶寺城址祭祀区大型建筑基址 2003年发掘简报[J].考古,2004,(7):9—24.
8 李勇.月龄历谱与夏商周年代(夏商周断代工程丛书)[M].北京:世界图书出版公司北京公司,2004.1—160.
9 Stephenson F R,Morrison L V.Long-Ter m Fluctuations in the Earth's Rotation:700 BC to AD 1990[J].Philosophical Transactions of the Royal Society of London,Ser.A,1995,351:165—202.
10 陈久金.试论陶寺祭祀遗址揭示的五行历[J].自然科学史研究,2007,26(3):324—333.
11 李勇.北斗观象授时系统[J].南京大学学报 (自然科学版),1991,27(4):653—659.
12 武家璧,陈美东,刘次沅.陶寺观象台遗址的天文功能与年代[J].中国科学 G辑,2008,38(9):1265—1272.
Abstract TaosiObservatory,possibly the earliest observatory possibly in the world,was found in 2005 in Taosi Town of Xiangfen City located in Shanxi Province.It has a sector structure and consists of one observing center and twelve observing slots.In order to investigate its essential conditions as a typical ancient observatory,and by referring to modern observations to imitate ancientworks on this site,the contemporary astronomical system are employed to simulate the scheme when the sun just rose from behind the top of remote mountains between 3000 BC and 1000 BC.It is obtained that the possible observing years of this observatory were earlier than 1500 BC and ascertained that 1956 BC is the best year.There all 12 slots could observe 21 times in one tropical year and the average error is about 0°.11 for per slot and the biggest error is 0°.7.The mean errors are 4.5 days from the observing dates to their neighborhood solar terms.The purpose of the ancient observatory is ascertained to be more likely to survey and investigate the particular dates of Taosi culture which perhaps related to the original of afterwards 24 solar terms,or to provide the accurate times for sacrifice or other important events.But because of having neither the main buildings above the earth surface nor other known document information,it is hard to give detailed information or precise deductions.
Key words astroarchaeology,Taosi town,observatory site,observing years
The Earliest TaosiObservatory and Its Possible Observing Years
LI Yong
(National Astronom ical Observatories,Chinese Academy of Sciences,Beijing100012,China)
N092∶P1-092
A
1000-0224(2010)03-0259-12
2009-09-13;
2010-04-26
李勇,1963年生,四川人,理学博士,中国科学院国家天文台研究员,主要从事天文年代学、天文历法、天文考古学、天文地球动力学等方面的研究。
国家自然科学基金(项目批准号:10973022)
