FLAC在水平层状岩体隧道围岩稳定性分析中的应用
2010-10-27邓少军苟德明阳军生
邓少军 苟德明 阳军生
1.贵州省交通规划勘察设计研究院 550001
2.中南大学土木建筑学院 410075
FLAC在水平层状岩体隧道围岩稳定性分析中的应用
邓少军1苟德明1阳军生2
1.贵州省交通规划勘察设计研究院 550001
2.中南大学土木建筑学院 410075
位于湖南常吉高速公路上的雀儿溪隧道,所穿地段围岩为水平层状岩体。本文选取了一典型断面作为计算模型,运用FLAC2D软件,考虑层面的影响,对水平层状岩体隧道施工过程进行了数值模拟,通过对比分析计算结果和实测结果,发现FLAC能比较真实地模拟和反映水平层状岩体隧道施工过程中的一些实际情况,可靠性较高,是一种可行的数值分析方法。
FLAC;水平层状岩体;隧道;层面;数值模拟
1、引言
对于层状岩体,通常都具有明显的层面。层面的存在不仅使围岩的各向异性十分显著,同时造成了围岩的不连续性,使围岩的变形破坏和坍塌有其特殊的形态。当隧道埋深不大时,岩体的初始应力水平不高,岩体的潜在破坏方式主要取决于岩体本身的特性。如果岩石坚硬或较坚硬,一般而言,结构面对岩体的潜在破坏方式起决定性作用[2]。因此,层状围岩的变形、破坏很大程度上受层面控制,在研究层状岩体围岩稳定性时有必要考虑层面的影响。
近年来,数值计算已经被普遍应用于工程设计中解决各种岩石力学问题,各种数值模拟技术在岩土力学中有了很大的发展和广泛的应用。然而,这些数值分析方法其理论本身以及采用的算法都有着各自的局限性。例如有限元和边界元都有小变形的假设,且需大量的内存。国内现用的离散元程序一般又很难考虑复杂的本构关系且其迭代求解所花时间相当可观。而快速拉格朗日分析(Fast Lagrangian Analysis of Continua,简称FLAC),则是在较好地吸取上述方法的优点和克服其缺点的基础上形成的一种数值分析方法。
FLAC首先由Cundall在80年代提出并将其程序化、实用化。FLAC基本原理类同于离散单元法,但它却能像有限元那样适用于多种材料模式与边界条件的非规则区域的连续问题求解;在求解过程中,FLAC又采用了离散元的动态松弛法,不需求解大型联立方程组(刚度矩阵),便于在微机上实现。另一方面,同以往的差分分析相比,FLAC在以下几方面作了较大改进和发展:它不但能处理一般的大变形问题,而且能模拟岩体沿某一弱面产生的滑动变形。FLAC还能针对不同材料特性,使用相应的本构方程来比较真实地反映实际材料的动态行为。此外,该数值分析方法还可考虑锚杆等支护结构与围岩的相互作用。
本文选取雀儿溪隧道一典型断面作为计算模型,运用FLAC2D软件,考虑层面的影响,对水平层状岩体隧道施工过程进行了数值模拟,通过对比分析计算结果和实测结果,验证该数值分析模型的可靠性。
2、数值模拟
2.1 工程概况
雀儿溪隧道是常吉高速公路上的一座分离式隧道,在进口段为近间距。本次分析选取的典型断面里程为YK193+730,位于其右线进口地段。该断面所处围岩级别为Ⅴ级,岩性主要为钙泥质砂岩与钙质砂岩互层,中厚层状,层间结合较差,其中:0~3.3m为强风化钙泥质砂岩,岩质较软,节理裂隙发育,岩石破碎,其他为弱风岩。设计中,采用复合式衬砌,初期支护由系统锚杆、单层钢筋网、喷射混凝土、工字钢钢拱架组成,结合超前小导管,模筑钢筋混凝土作为二次衬砌,其中初衬采用C20喷射混凝土,厚度为26cm,18型工字钢钢拱架间距为75cm,二次衬砌采用C25钢筋混凝土,厚度为50cm。施工时采用上下台阶法进行施工,图1和图2分别为该断面的岩层分布柱状图和断面支护图。

图1 隧道岩层柱状图
2.2 模型的建立
依照地质资料,以及设计中隧道断面的相关尺寸建立平面应变模型,计算模型的宽度为150m,垂直方向上,仰拱底部往下取30m,而隧道上方按实际地形尺寸。计算时所施加的边界约束条件是:地表为自由边界,未受任何约束;计算模型的左右边界分别受到水平方向的位移约束,下部边界受到垂直和水平方向的位移约束。计算模型网格划分如图3所示。
分析时,采用平面应变模型,各岩层采用Mohr-Coulomb屈服准则,层面采用接触面单元,初始应力仅考虑自重应力,隧道初期支护考虑锚杆、喷射混凝土以及钢拱架的作用,钢筋网、纵向连接筋等对喷射混凝土力学性质的贡献作为安全储备,不予考虑。围岩采用四边形等参单元,锚杆采用杆单元,初衬及二衬采用梁单元,初衬和二衬之间的防水层采用接触面单元。地应力的释放采用施加虚拟支撑力的办法进行模拟,本模型中设定开挖瞬间地应力释放率为30%,初期支护完成后

图2 隧道支护断面图

表1 数值分析计算参数
表中:E—弹性模量;γ—容重;μ—泊松比;c —粘结力;φ—内摩擦角;σt —岩体抗拉强度;Kbond—灰浆剪切刚度;Sbond—杆体与围岩间的粘结力;Yield—为钢筋的抗拉屈服力;Area—面积;I—惯性矩;kn—正压刚度;ks—剪切刚度。释放40%,二衬完成后释放其余30%。

图3 计算模型网格图
2.3 计算参数的确定
弱风化钙质砂岩、弱风化钙泥质砂岩的力学参数根据现场取样和岩石力学实验结果,考虑实际节理裂隙发育情况,通过霍克-布朗方法进行弱化,强风化钙泥质砂岩的力学参数通过地质勘察资料获得,层面的参数则通过工程类比的方法确定[3][4]。锚杆和混凝土衬砌具体几何参数为实际施工的数值,其力学参数依据文献[3]、[5]中相关参数的确定方法予以确定。
钢拱架的作用则采用等效方法予以考虑,即将钢拱架弹性模量折算给喷射混凝土,计算公式为[6]:
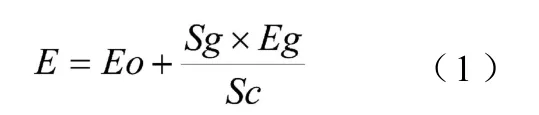
式中:E为折算后混凝土的弹性模量;Eo为原混凝土的弹性模量;Sg为钢拱架的截面积;Eg为钢材的弹性模量;Sc为混凝土的截面积。
折算后,喷射混凝土的弹性模量取为24.3Gpa,其余参数见表1。
2.4 施工过程的模拟
施工中左右洞均采用上下台阶分部开挖方法,先开挖左洞,后开挖右洞。根据实际施工步骤,计算中把整个施工过程分为9步加以仿真模拟分析:第0步(初始状态)→第1步(左洞开挖上台阶)→第2步(对左洞上台阶的开挖部分进行喷锚支护)→第3步(左洞开挖下台阶)→第4步(对左洞下台阶的开挖部分进行喷锚支护)→第5步(右洞开挖上台阶)→第6步(对右洞上台阶的开挖部分进行喷锚支护)→ 第7步(右洞开挖下台阶)→第8步(对右洞下台阶的开挖部分进行喷锚支护)→第9步(右洞施作全断面二次衬砌混凝土)。
3、计算结果与实测结果的对比
3.1 拱顶下沉值的对比
图4示出了量测断面YK193+730的累计拱顶下沉值随时间的变化曲线,从图中可以看出,拱顶沉降显著的情况出现在其上台阶开挖的时候,上台阶开挖支护后,拱顶垂直位移为3.19mm,该断面最终拱顶累计下沉值为4.33mm。
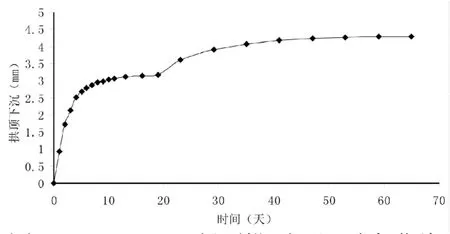
图4 YK193+730断面拱顶下沉时态曲线
图5示出了拱顶在施工过程中垂直位移变化的数值模拟结果。从图中可以看出,位移值为负,说明隧道拱顶发生向下的垂直位移,最终垂直位移值收敛于3.42mm,与现场实测值(4.33mm)比较接近。拱顶沉降显著的情况也是出现在其上台阶开挖的时候,上台阶开挖支护后,拱顶垂直位移为2.29mm, 占最终沉降量的66.8%,这与现场实测值(73.7%)也比较接近。

图5 拱顶垂直位移变化与迭代次数关系曲线
3.2 二次衬砌内力的对比
为了解二次衬砌的内力大小和分布规律,在量测断面YK193+730二衬内外侧埋设应变计。其埋设位置如图6所示。

图6 应变计布置示意图
图7和图8分别示出了2005年11月20日测出的二衬轴力和弯矩分布状况。图9和图10分别示出了二衬计算轴力和计算弯矩分布状况。从二衬轴力分布图中可以看出,二衬轴力计算结果和实测结果均呈现出拱部小边墙大的分布规律,这主要是因为施工中采用的是上下台阶法施工,在施作二衬时拱部应力释放已较充分,二次衬砌的荷载分担比例较小的缘故。从二衬弯矩分布图来看,数值计算结果要大于现场测试结果,但从分布规律上来看,数值计算和现场测试均表明,最大弯矩出现在右墙脚处,隧道拱顶处出现了负弯矩。

图7 二衬实测轴力分布图(KN)
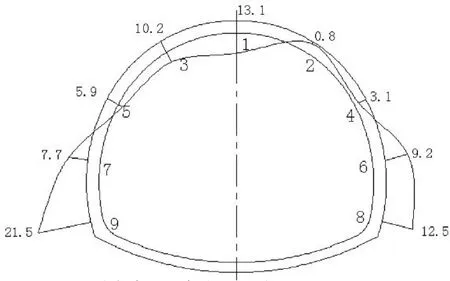
图8 二衬实测弯矩分布图(KN·M)

图9 二衬计算轴力分布图(KN)
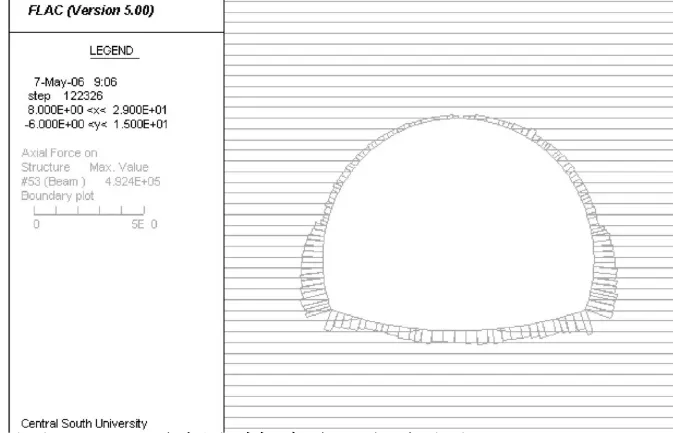
图10 二衬计算弯矩分布图(KN·M)
4、结论
尽管数值分析方法能较全面的考虑实际情况,但是由于岩土工程问题的复杂性,加之施工方法和现场工序的多变,计算结果未必能真实反映围岩和衬砌结构的实际受力性态,现场测试也由于元件的客观存在及其测试精度而使得元件布设位置测试结果会与本来真实情况产生偏差。因此,数值计算结果与实测结果存在偏差也就在所难免。
通过上述计算实例及其计算结果与实测结果的对比可以知道,计算结果与实测结果虽然存在偏差,但是有些地方符合较好,说明采用FLAC能够比较真实地模拟和反映水平层状岩体隧道施工过程中的一些实际情况,可靠性较高,是一种可行的数值分析方法。
[1] Itasca Consulting Group, Inc. FLAC2D, Fast Lagrangian Analysis of Continua, version 5.00,user’s manual. USA:Itasca Consulting Group, Inc., 2005.
[2] 朱焕春,Brummer Richard,Andrieux Patrick. 节理岩体数值计算方法及其应用(一):方法与讨论. 岩石力学与工程学报.2004,23(20):3444~3449
[3] 中华人民共和国交通部. 公路隧道设计规范(JTG D70—2004). 北京:人民交通出版社.2004-11-01
[4] 林崇德. 层状岩石顶板破坏机理数值模拟过程分析. 岩石力学与工程学报.1999,18(4):392~396
[5] 刘波,韩彦辉. FLAC原理、实例与应用指南. 北京:人民交通出版社.2005
[6] 李凤刚.黄土连拱隧道施工过程的数值模拟和方案优化[B].安徽建筑.2003,(3):87~89.
[7] 邓少军. 水平层状岩体隧道围岩稳定及支护参数优化研究:[硕士学位论文].长沙:中南大学.2006
邓少军(1979-),男,硕士,工程师,主要从事隧道及地下工程方面的设计研究工作。
