未知环境下基于三次螺线Bug算法的移动机器人路径规划

康 亮， 赵春霞， 郭剑辉

（南京理工大学计算机与科学技术学院，江苏 南京 210094）

移动机器人技术是近年来发展起来的一门综合学科，集中了机械、电子、计算机、自动控制以及人工智能等多学科最新研究成果，代表了机电一体化的最高成就[1]。在移动机器人相关技术的研究中，导航技术是其核心，而机器人路径规划是解决机器人导航的核心问题之一。

移动机器人路径规划可以分为两类：一类是基于已知或部分已知数字地图的全局路径规划[2]；另一类是基于传感器信息的局部路径规划[3-5]。很多实际情况下，机器人并不具备完备的环境知识和复杂的障碍物信息。因为未知的障碍物可能出现在事先规划好的路径上，这样机器人导航系统中需要基于传感器信息的，以在线方式进行避碰规划。此时，Bug算法[6]在实际中被应用。这种算法是完备的。如果在机器人起点和目标终点间存在可行路径的话，那么这种纯粹的应激式算法肯定会完成路径规划，保证算法的全局收敛。但这种算法却不能保证规划路径的光滑，这在实际应用中会使得移动机器人执行起来很困难，精度下降。而曲率连续对于非完整移动机器人路径设计是最基本的。

作为非完整移动机器人控制任务之一的路径规划，由于先规划出来的路径可能由若干线段组成，而且线段之间可能出现不连续。为了避免移动机器人在运动过程中产生滑动现象而降低机器人的实时到达性，有必要将路径光滑化。路径光滑的任务就是寻求一种连接移动机器人任意两个姿态的曲线，对于时间和长度都是最优的。在没有解决曲线路径跟踪难题之前，一般就是用直线来连接各个姿态。直线连接实现简单，路径长度最短，但需要移动机器人频繁地停止以改变方向，灵活性不够。后来使用直线-圆弧-直线的连接方案使得移动机器人的灵活性得到提高。此算法中一个主要问题是生成路径的曲率不能连续。在直线与圆弧的连接点处，曲线的曲率会发生跳变，移动机器人的角速度等参数也随之发生跳变。因此，当移动机器人进行路径跟踪时跟踪精度必然受到影响。故严格意义上讲，机器人是不能平滑跟踪路径的。

本文考虑未知环境下移动机器人的路径规划。将Bug算法与基于滚动窗口的路径规划相结合，先由路径规划器产生一条局部无碰撞可行路径，再利用三次螺线对滚动窗口内已规划的路径光滑化，从而使得移动机器人易于跟踪所规划的路径，随滚动窗口的推进来完成未知环境下的移动机器人路径规划。

三次螺线[7]（cubic spiral）是一种曲线。这种类型的曲线有连续曲率变化，切线方向由路径距离的三次方函数描述。三次螺线与直线连接时曲率连续，生成的路径满足几何学特性，符合移动机器人动力学特性。结果显示三次螺线在路径最大曲率处是较好的。同时三次螺线的各个参量容易得到，满足移动机器人实时性计算的要求。

1 Bug算法

在Bug算法中，移动机器人沿连接目标点和起点的最短直线前进，在遇到障碍物时采用边缘跟踪的方法绕过障碍物，然后再次沿直线前进。Bug算法在移动机器人未知环境导航中是经典通用的算法。需求的存储容量小。如果在机器人起点和目标终点间存在可行路径的话，那么这种纯粹的应激式算法肯定会完成路径规划，保证算法的全局收敛。

Bug算法在寻找两点间可行路径上并不能保证最优。标准的算法是在起点和终点的直线方向上产生，遇到障碍物时沿相同的方向绕行。这种算法能保证寻找到一条安全路径，但并不保证能迅速到达目标终点，如图1所示。

图1 标准的Bug算法

Bug算法由两种模式来共同保证全局收敛：趋向目标模式（Moving toward the Goal）和边线沿走模式（Boundary Following）。开始时移动机器人执行“趋向目标”模式，遇到障碍物时转向“边线沿走”模式。

1.1 趋向目标模式

趋向目标模式的目的是使机器人以到目标点的距离单调递减的方式向目标点运动，从而保证全局收敛。在此模式下，机器人或者在自由区域直接向目标运动或者绕过障碍物向目标运动。

机器人沿直线移动，趋向目标，直到发生下列情况：① 到达目标，移动终止；② 如果移动机器人遇到障碍物，则转入“边线沿走模式”。

1.2 边线沿走模式

边线沿走模式的目的是绕过障碍物，使得机器人可以继续向目标点运动。此时需要机器人选择较优的绕行方向，而错误的绕行方向常常严重增加路径长度，降低效率。

标准的Bug算法是遇到障碍物时永远沿相同的方向绕行。Distbug算法[8]对Bug算法进行了改进：机器人用符号化的累积参数Dir来选择遇到障碍时的绕行方向，Dir为正数表示左侧可安全通行的区域更大，应选择左侧绕行；反之则选择右侧绕行。Tangentbug算法[9]选择最小化距离作为绕行方向，直到发生下列情况：① 到达目标，移动终止；② 满足算法提出的离开条件，转入“趋向目标模式”；③ 机器人绕障碍物闭合循环一周，则宣布目标无法到达，移动终止。

由图1可看出，原始标准Bug算法使用传感器数据信息生成的路径并不是最优路径，它需要改进。而且该算法有个前提是假设机器人为一个质点，没有实际尺寸。可在实际的机器人研究中，这个假设总是不成立。因为大多数移动机器人为非完整移动机器人，对所规划路径有一定的要求。曲率不连续的路径很难保证机器人跟踪所规划的路径。这在图1中就可以看到。机器人在两种行为模式转换时，规划路径曲率发生跳变。移动方向的突然变化使得移动机器人的角速度等参数也随之发生跳变，则移动机器人进行路径跟踪时跟踪精度必然受到影响。

同时，作为非完整移动机器人，在实际的系统执行中，方向角度变化不可能太大。当转变的方向角度为90°时，轮式移动机器人的前轮会和两前轮之间的轴碰撞，也就是说机械装置把方向角限制在一个特定的范围之内。这要求系统路径规划器能规划出平滑的路径来适应实际需要。

2 三次螺线

路径的平滑对于移动机器人导航是最基本的，因为不平滑的运动可能会导致轮子打滑，而这会降低机器人刹车能力。为了控制路径的平滑性，本文定义了路径平滑的成本函数：路径曲率导数的平方。通过定义，得到三次螺线的简单路径。Boissonnat[10]采用直线和圆弧来描述路径，并做了很多研究。然而，此算法中一个主要问题是生成路径的曲率不能连续。因此，严格意义上讲，移动机器人是不能平滑跟踪路径的。三次螺线是一种曲线。它的切线方向由路径距离的三次方函数描述。这种类型的曲线有连续曲率变化，生成路径满足几何学特性，符合移动机器人动力学特性，可以扩展移动机器人的应用。同时三次螺线的各个参量容易得到，满足移动机器人实时计算的要求。

2.1 相关定义

本文描述了一种平滑局部路径的算法，是通过一连串二维世界坐标系中移动机器人位姿（位置和方向）代替一连串曲线段来描述路径。在连接给出位姿(x,y,θ)的同时，平滑移动机器人的路径。

定义p1=(x1,y1,θ1)，p2= (x2,y2,θ2)是移动机器人的两个路径位姿节点，此时(x1,y1)≠ (x2,y2)。从点(x1,y1)到点(x2,y2)的方向β为

如果以下关系满足，则两个位姿p1和p2被称为对称。

如果两个位姿p1和p2对称，记为sym(p1,p2)，否则记为 ～sym(p1,p2)。

对称位姿(p1,p2)的大小d和偏差α被定义为两点间欧式距离平方和两点方向角的差值

d=((x2-x1)2+(y2-y1)2)，α=θ2-θ1

如果sym(p1,q)和sym(q,p2)，则位姿q被称为(p1,p2)的切分位姿。

定义一个有限长度的封闭路径表示法。路径Π是一对(l,k)。其中l是正的路径长度，k是连续曲率函数。曲率在(x(s),y(s) )处的曲线半径和切线方向导数。函数θ由下式给出

如果曲率函数k是对称的，也就是如果k(-s)=k(s)，则对于所有s，有以下关系

路径点 (x,y)= (x(s),y(s))由下式给出

在平滑路径过程中，须定义一个关于路径平滑度的成本函数。对于每一个路径Π，路径平滑成本cost(Π)是明确具体的。这里定义路径平滑的成本函数为

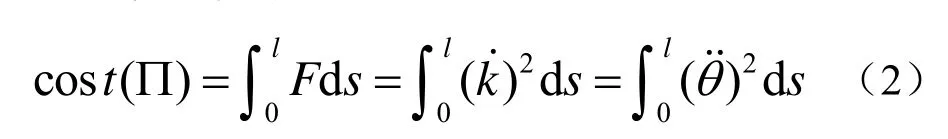
根据路径上两个位姿点的关系情况，可以分为以下两种情况：

（1） 如果sym(p1,p2)，在具有同样大小和偏差的(p1,p2)集合S中寻找路径，确定适当的平移和旋转来适应末端位姿。这种合成的简单路径表示为 Π (p1,p2)。注意，大小和偏差就完全描述了一个简单路径。

（2） 如果 ～sym(p1,p2)，首先，寻找(p1,p2)的切分轨迹，接着寻找切分位姿q，使得 成 本 总 和 cost(Π(p1,q))+cost(Π(q,p2))是最小的。

2.2 位姿对称

根据路径平滑成本函数，使得方程（2）的路径平滑成本最小，将路径分类。

对于固定路径长度l，以路径曲率导数的平方为路径平滑成本函数。取路径平滑成本函数cost(Π )最小，通过解方程（2）可以得到

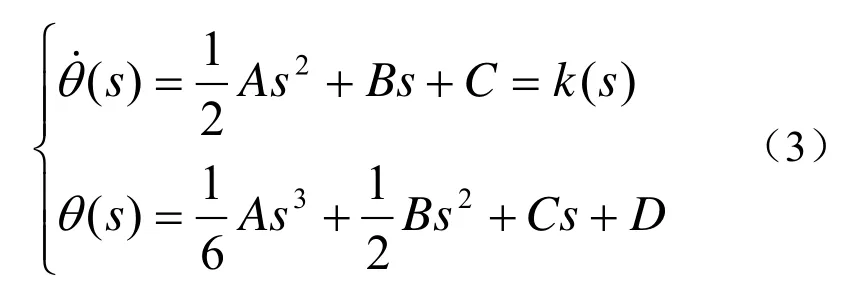
这里的A、B、C、D是积分常数。因为上式描述的方向函数θ是三次方函数，所以称这类路径曲线为三次螺线，其曲率是连续的。

当两个位姿p1和p2是对称情况时，(p1,p2)的大小d和偏移α被给出。在平滑路径规划问题中，用三次螺线来连接两个对称位姿点，则三次螺线的长度、曲率和成本表达式为

这里的θ0是常数。其中

2.3 位姿非对称

当输入位姿p1=(x1,y1,θ1)，p2=(x2,y2,θ2)是非对称时，根据方向角关系，将(p1,p2)分两种 情 况 。 这 里 (x1,y1)≠ (x2,y2)。当且仅当θ1=θ2时，(p1,p2)被称为平行的，否则称为不平行。根据sym(p1,q)和sym(q,p2)，寻找切分位姿q，使得成本总和 cost(Π(p1,q))+cost(Π(q,p2))是最小的。则q(x,y,θ)点的位置是：

（1） 如果(p1,p2)是平行的，则由点p1和p2来确定直线

（2） 如果(p1,p2)不是平行的，通过点p1和p2的曲线为

对于路径平滑成本函数，当θ=θ1=θ2，(p1,p2)是平行时，取成本总和cost(Π(p1,q))+cost(Π(q,p2))是最小，则切分位姿q点是

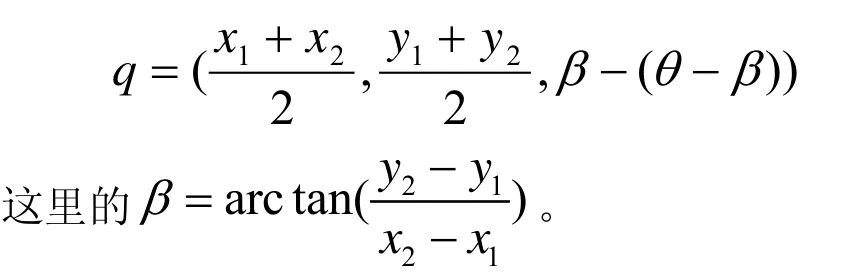
当(p1,p2)不是平行时，切分点q位于方程（5）曲线中，使成本总和 cost(Π (p1,q))+cost(Π (q,p2))是最小。因为没有解析方法，这里采用Newton-Raphson迭代算法来寻找最小值。

3 三次螺线Bug算法

本文改进Bug算法的缺点，通过构建滚动窗口，选择较优的路径节点，利用上节所述的三次螺线来平滑路径。最终随着滚动窗口的推进，移动机器人能够沿规划的平滑路径，在未知环境中到达目标位置。

3.1 滚动窗口构建

信息不完全、环境不确定情况下的路径规划问题，是传统全局规划方法无法解决的。注意到机器人在运动过程中能探知其传感范围内一有限区域的环境信息，这部分信息必须充分利用。因此，解决这一问题的指导思想是：采用反复进行的局部优化规划代替一次性的全局优化的结果，并在每次局部优化中充分利用该时刻最新的局部环境信息[11]。

以周期方式驱动，在滚动的每一步，定义以机器人当前位置为中心的一区域为优化窗口。Win(PR(t) )= {P|P∈W,d(P,PR(t) )≤r} 称为机器人在PR(t)处的视野域，亦即该点的滚动窗口，其中PR(t)为机器人工作环境中的可行区域，r为机器人传感器的探测半径，W为机器人的工作环境。

局部子目标最优点Oi和最短路径由启发式函数l(x,G)=min(l(x,Oi)+d(Oi,G))决定。这种子目标的选择方法反映了全局优化的要求与局部有限信息约束的折衷，是在给定信息环境下企图实现全局优化的自然选择。

该区域内的预测模型一方面是全局环境信息向该区域的映射，另一方面还补充了传感器系统检测到的原来未知的障碍物。以当前点为起点，根据全局先验信息采用本文的启发式方法确定该窗口区域的局部目标，根据窗口内信息所提供的场景预测进行规划，找出适当的局部路径，机器人依此路径移动，直到下一周期。

3.2 趋向目标模式

首先判断机器人和给定的目标位置之间是否存在障碍物。传感器输入是机器人当前位置和在传感器探测半径范围内机器人与障碍物的距离。机器人扫描直接指向目标的扇形，并以此扇形区域作为机器人滚动窗口来搜索路径。扇形半径是机器人的探测半径，扇形弦长为机器人的碰撞直径，本文取机器人正前方3个传感器的探测区域。

以G代表目标位置，其坐标为(xG，yG)，以R、O分别代表机器人及障碍物，坐标为(xR，yR)、(xO，yO)。设置机器人和障碍物的碰撞半径，也就是说在其半径以外无碰撞的危险，保证规划的路径宽度。若机器人与目标位置之间不存在障碍物，机器人可按“趋向目标”模式直接到达目标位置。此时的直线方程可由两点式确定

在趋向目标直线行走模式下，机器人只利用指向目标点的扇形区域内的探测数据来作为滚动窗口数据信息规划路径。当此扇形区域内出现障碍物时机器人需扩展探测区域，规划绕行路径。本文是将扇形区域扩展为机器人周身360°的探测圆，作为滚动规划窗口。

当机器人探测到障碍物时，如果障碍物位于预规划的前进路径，则取消原来的直线行进计划，改为沿三次螺线靠近障碍物向目标前进。此三次螺线为机器人当前点与所探测到障碍物边界登陆点之间的三次螺线。

当下列条件满足时，“趋向目标”模式结束：

（1） 机器人到达目标点，算法停止；

（2） 机器人探测到障碍物阻挡前进路径，切换到“边线沿走”模式。

3.3 边线沿走模式

首先定义两个概念：① 登陆点：滚动窗口内可见的障碍物上最近的顶点。② 分离点：绕过障碍物时探索线的起点。

如图2所示，当移动机器人沿直线前进，如果传感器探测到障碍物，则障碍物可见边界的顶点必定分布在直线路径的两侧。把障碍物可见边界的顶点分成两组。图中以蓝色小圆圈表示。直线左侧的顶点归入L组，右侧的归入R组。另设OL和OR分别是L和R组中离原来路径最远的两个顶点。

根据距离长度公式li=l(x,Oi)+d(Oi,G)，Oi分别是OL和OR。l(x,Oi)为当前机器人到Oi点的三次螺线长度。d(Oi,G)为障碍物Oi点到目标终点G的直线距离。引入d(Oi,G)是为了保证机器人所规划的路径能够全局收敛，不至于因为局部信息的不完整而导致非全局最优的路径。如果lR＜lL，则令C=R，否则令C=L。OC就是登陆点。移动机器人绕障碍物行走时首先向登陆点靠近。

图2 探测到障碍物

如果移动机器人滚动窗口内探测到身处多个障碍物包围中，结合上文，利用以下距离长度公式在探测到的各个障碍物边界中求登陆点

其中Oi分别为移动机器人能够探测到的各个障碍物可见边界的顶点，l(x,G)表示在探测到的各个障碍物登陆点中机器人距离目标最短路径的长度。移动机器人选择路径最短的顶点作为下一步运动的登陆点。如上所述，l(x,G)的计算表达式反映了机器人的全局意识，保证了算法路径规划中的全局收敛。

移动机器人找到登陆点后，就开始规划如何绕过障碍物。先把机器人与登陆点用三次螺线方程连接，再把登陆点OC与目标连接起来。视OC为当前点，记做P。如果机器人在此处的滚动窗口内没有探测到障碍物，表明已绕过了障碍物，称此P点为移动机器人绕过障碍物的分离点，否则把当前登陆点从P出发沿着障碍物边界移到机器人探测到的障碍物边界下一个节点上，进入“边线沿走”模式。同时由距离长度公式li=l(x,Oi)+d(Oi,G)，不断选择窗口内的最佳的局部路径目标点。

当满足下列条件时，“边线沿走”模式结束：

（1） 到达目标点，算法结束；

（2） 满足离开条件，探测不到障碍物，切换到“趋向目标”模式。

离开条件为当上一个登陆节点到目标终点距离大于机器人其他传感器定位点到目标终点的距离时，算法选择距离最小值的传感器定位点为机器人路径的下一节点，同时模式切换为趋向目标模式。

4 仿真实验

算法验证采用四轮移动式机器人。机器人在运行环境中的定位由GPS完成。测距系统是由安装在机器人车体前后的16个超声波传感器来实现，用来提供机器人周围的障碍物距离信息。路径规划算法由主机完成，规划完成后把控制命令发给机器人，使它在运行环境中移动。

这里有一个对比实验。当取路径平滑成本函数为路径节点曲率的平方时，即

则将成本函数最小化，可得方向函数θ(s)=As+B，分别代入圆弧方程和回旋螺线方程

图3是偏差α是π的两个位姿的连接情况。分别用圆弧、三次螺线和回旋螺线来平滑路径。可以看到，圆弧连接时曲线长度最小，回旋螺线连接时曲线长度最大。相比于圆弧连接的曲率不连续和回旋螺线连接的曲线长度最大，三次螺线是两个路径位姿点用于平滑路径的最佳选择。

移动机器人路径规划仿真环境是用matlab开发的，运行于PC机，CPU主频512M。起始点和终点位姿分别是(0,0,π/4)，(30,30,π/4)。在30×30(m)环境下的路径规划结果如图4所示。

图3 方向偏差为π时的曲线连接

图4 路径规划结果比较

图4显示了分别利用标准Bug算法和用本文三次螺线Bug算法及回旋螺线Bug算法来规划路径的结果比较。无论在趋向目标模式还是边线沿走模式，传统Bug算法都有严格规定，不能随意改变方向。从图4试验结果来看，本文构造滚动窗口时，搜索机器人周围各点的最佳行走方向，考虑全局收敛标准，因此可以在任何模式下都能根据具体情况，按照最佳的行走方向来规划路径，提高了路径的优化性。同时由于三次螺线的使用，使规划路径曲率连续，移动机器人跟踪精度得到明显改善，直线与三次螺线连接处平滑过渡，可以规划出光滑的路径，实现了四轮移动机器人连续的移动。表1给出了相关算法在图4环境中的路径规划结果对比。

表1 算法性能对照表

结合表1，从图4中看到无论是长度还是运行时间，本文算法都比标准Bug算法要较优。而且标准Bug算法的路径曲率不连续，不能应用于非完整移动机器人。回旋螺线虽然可以保证曲率连续使路径平滑，但规划的路径长度却增加，运行时间也同比增长。本文算法既满足了规划路径曲率连续，保证机器人运动平滑，同时在路径长度和运行时间上达到了综合最优。图5是利用本文算法的移动机器人在复杂环境中的路径规划结果，更清晰显示了路径的光滑性。

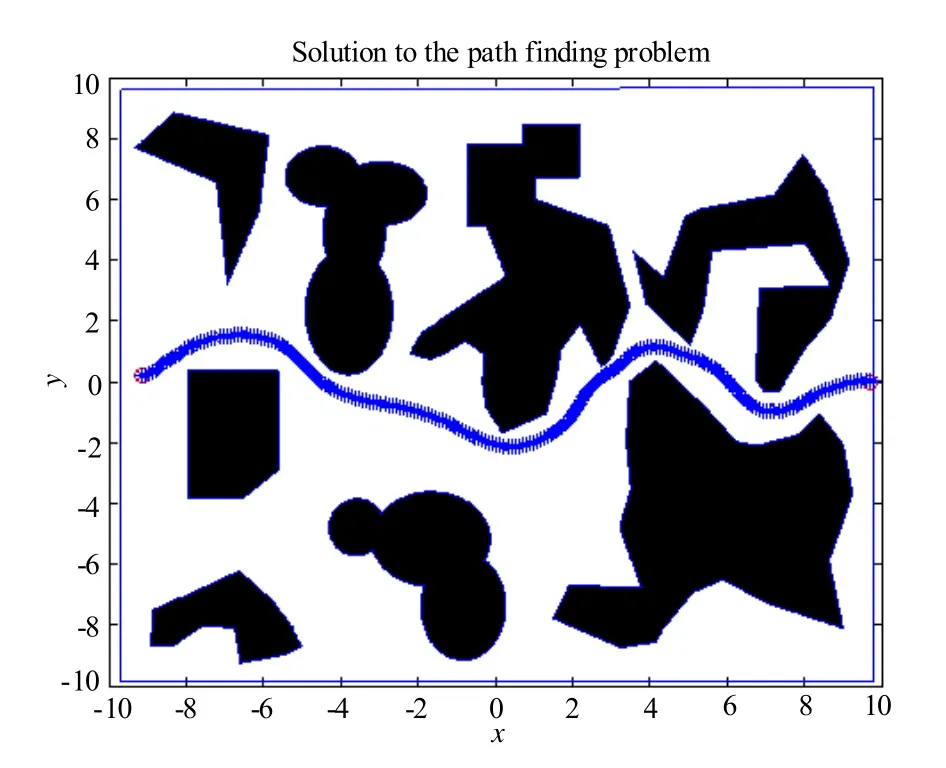
图5 路径规划结果

5 收敛性和完备性证明

在趋向目标模式中，距离函数d(x,G)是单调递减的，因而此模式下的路径长度是有限的。在边线沿走模式中，总是选择距离长度最小值节点为规划路径下一节点，因而此模式下的每一步路径长度也是有限的。因此，算法最终会在一个有限长度的路径上停止。如果目标终点可以到达，那么规划路径收敛到目标终点的可能性就会得到保证。

首先定义机器人路径是由一连串的节点组成。起点S，目标终点G。登陆点Hi是机器人首先探测到障碍物时的路径节点。离开点Di是在趋向目标模式中机器人开始远离障碍物边界时的路径节点。转换节点Pi为机器人从趋向目标模式转为边线沿走模式时的节点。每一个转换节点一定也是属于l(x,G)的局部极值点Mi。转换离开节点Li为机器人从边线沿走模式转为趋向目标模式时的路径节点。

假设机器人工作在一个有限的几何空间中，环境空间中的每一个障碍物都是有限周长，因此有以下结论：

（1） 机器人趋向目标模式的路径片断必定会终止在目标点G，或者终止在局部极值点Mi。

（2） 在趋向目标模式中，路径长度必定是有限长度。

（3） 如果从局部极值点可以到达目标终点，那么由于l(x,G)=min(l(x,Oi)+d(Oi,G))，机器人离开障碍物的路径长度将是有限长度。

下面给出算法的收敛性证明：如果移动机器人可以到达目标，那么成功规划的路径长度必定是有限长度。

证明：机器人的路径长度等于趋向目标模式下和边线沿走模式下的路径长度之和。由结论（2），在趋向目标模式中，机器人路径长度必定是有限长度。因为机器人工作在一个有限的几何空间中，所以障碍物的个数也必定是有限的。而每一个障碍物又都是有限周长，所以在边线沿走模式中，机器人的路径长度也必定是有限长度。由结论（3），如果机器人可以从局部极值点到达目标终点，那么机器人离开障碍物的路径长度也必将是有限长度。

因此，算法成功规划的路径长度必定是有限长度。

下面再给出算法的完备性证明：只要移动机器人可以到达目标，那么算法必定可以规划出从起点到终点的路径。

证明：由结论（1），趋向目标模式中的每一个机器人路径片断都必定会终止在目标点G，或者终止在局部极值点Mi。当发现局部极小值点Mi时，机器人转为边线沿走模式。如果目标是可以到达的，那么由结论（3），绕障碍物行走模式必定会终止在转换离开节点Li。因为机器人工作空间有限，则障碍物个数也必定是有限个数，所以绕障碍物行走模式下的最终路径会是趋向目标模式下的路径片断。因此，最终的路径必定会终止在目标点。由此证明了算法的完备性。

6 结 论

本文考虑未知环境下移动机器人的路径规划。将Bug算法与基于滚动窗口的路径规划相结合，先由路径规划器生成一条局部无碰撞可行路径，再利用三次螺线对滚动窗口内已规划的路径光滑化，从而使得移动机器人易于跟踪所规划的路径，随滚动窗口的推进来完成未知环境下的移动机器人路径规划。

在原有Bug算法基础上，本文搜索机器人周围各点的最佳行走方向，考虑引入的全局收敛标准，因此可以在任何模式下都能根据具体情况，按照最佳的行走方向来规划路径，提高了路径的优化性。

三次螺线与直线连接时曲率连续，生成的路径满足几何学特性，符合移动机器人动力学特性，曲率有界。同时三次螺线的各个参量容易得到，满足移动机器人实时性计算的要求。这种类型的曲线有连续曲率变化，可以扩展移动机器人的应用。本文中，给出了机器人路径平滑成本函数。路径平滑成本是路径曲率导数平方。通过对比实验，在克服了圆弧曲线连接曲率不连续的基础上，可知机器人的运动要比沿回旋曲线平滑，路径长度也相应降低，证明三次螺线在路径平滑上是不错的选择方法。

[1]孙迪生, 王 炎. 机器人控制技术[M]. 北京: 机械工业出版社, 1997. 6-10.

[2]Park M G, Jeon J H, Lee M C. Obstacle avoidance for mobile robots using artificial potential field approach with simulated annealing [C]//ISIE. Pusan,Korea, 2001: 1530-1535.

[3]Faisal S, Raja Q S. Path finder in unknown environment [C]//IEEE International Conf. on Emerging Technologies. Peshawar, Pakistan, 2006:575-580.

[4]唐振民, 赵春霞, 杨静宇, 等. 地面自主平台的局部路径规划[J]. 机器人, 2001, 23(7): 742-745.

[5]赵春霞, 唐振民, 陆建峰, 等. 面向自主车辆的局部路径规划仿真系统[J].南京理工大学学报,2002, 26(6): 570-574.

[6]Kamon I, Rivlin E, Rimon E. A new range-sensor based globally convergent navigation algorithm for mobile robots [C]//Proceedings of IEEE International Conf. on Robotics and Automation.Minneapolis, MN: IEEE Computer Society Press,1996: 22-28.

[7]Kanayama Y, Hartman B I. Smooth local path planning for autonomous vehicle [C]//Proceedings of Int’l Conf on Robotics and Automation. IEEE Publish Society. Scottsdale, Arizona, 1989:1265-1270.

[8]Kamon 1, Rivlin E. Sensory based motion planning with global proofs [C]//IROS'95. Pittsburgh, PA,USA, 1995: 435-440.

[9]Kamon I, Rivlin E, Rimon E. A new range-sensor based globally convergent navigation algorithm for mobile robots [C]//Proceeding of the 1996 IEEE International Conf. on Robotics and Automation.Minnesota, 1996(4): 429-435.

[10]Boissonnat J D, Cerezo A, Leblond J. Shortest paths of bounded curvature in the plane [C]//Proceedings of the IEEE International Conf. on Robotics and Automation. Piscataway, NJ, USA: IEEE, 1992:2315-2320.

[11]席裕庚. 动态不确定环境下广义控制问题的预测控制[J]. 控制理论与应用, 2007, 17(5): 665-670.