双谱在微弱信号检测中的应用

王凤歌,王辉,2,李晓荃

(1.中原工学院,郑州450007;2.郑州大学,郑州 450052)

双谱在微弱信号检测中的应用

王凤歌1,王辉1,2,李晓荃1

(1.中原工学院,郑州450007;2.郑州大学,郑州 450052)

根据高斯噪声双谱为零的特点,采用双谱分析法检测强噪声背景下的微弱信号.仿真结果表明,双谱分析法可以较好地抑制噪声信号,检测出有用信号.

高阶累积量;高阶累积量谱;噪声;检测方法

微弱信号不仅表示幅值很小的电信号,同时也指强噪声背景下的电信号[1].微弱信号检测是指通过一定的方法,对被噪声淹没的微弱有用信号进行提取和测量.微弱信号检测的目的是抑制噪声,恢复、增强和提取有用信号,提高信噪比.

传统的微弱信号推测理论和方法主要是采用似然比检验,但是似然比检验有2个明显的缺点:一是要求观测对象必须满足高斯条件的假设;二是当观测噪声的信噪比下降时,系统的检测性能急剧下降,很难得到较高的检测概率.随着现代信号处理技术的发展,各种新的理论方法不断出现,目前关于微弱信号检测的方法有很多,如基于混沌理论的微弱信号检测技术[2-3]、基于小波变换的微弱信号检测理论[4-5]、基于随机共振的微弱信号检测方法[5-7]等.

高阶谱分析是在相关函数、功率谱理论等二阶统计量的基础上发展起来,其中双谱(三阶矩谱)的研究最为深入.双谱可表示为3个傅里叶分量的乘积,其中一个频率为其他2个频率之和[8].和其他检测方法相比,高阶谱分析方法具有以下优点:①能够有效地检测信号幅度,还可以提供信号的相位等信息,因此可以用于非最小相位系统和信号的辨识;②可以抑制高斯噪声,提高信号参数估计性能;③能够检测和刻划信号的非线性特性或者辨识非线性系统;④可以提取随机过程偏离高斯分布的程度,用于信号的分类[9].

本文采用高阶谱中应用最广泛的双谱分析方法,来检测强噪声背景下的信号,仿真实验表明,该方法效果良好.

1 高阶统计量的定义

1.1 随机变量的特征函数与累积量

定义:设随机变量 x具有概率密度 f(x),其特征函数定义[10]为:

其中:s为特征函数的参数.特征函数Φ(s)只是参数s的函数.对Φ(s)求 k次导数,可得:

因此:

也就是说Φ(s)在原点的k阶导数等于x的k阶矩mk.因此,Φ(s)也称作矩生成函数(又叫第一特征函数).

由矩生成函数可以定义随机变量x的累积量生成函数(又叫第二特征函数)及累积量.

定义:设随机变量 x的矩生成函数为Φ(s),则

称为 x的累积量生成函数,而ψ(s)在原点的 k阶导数

称为 x的k阶累积量.

1.2 随机矢量的特征函数与累积量

定义:令 x=[x1,x2,…,xk]T是一随机矢量,且s=[s1,s2,…,sk]T,则随机矢量 x的矩生成函数定义为:

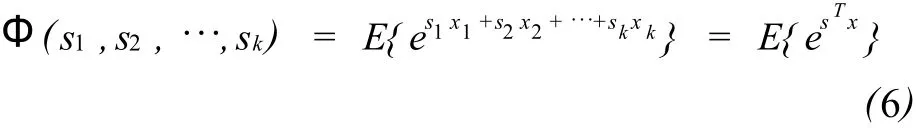
x的累积量生成函数定义为:

x的(v1,v2,…,vk)阶矩和累积量分别定义为矩生成函数和累积量生成函数的 Taylor级数展开中s1v1s2v2…svkk项的函数,即:

1.3 随机过程的高阶矩和高阶累积量

定义:设{x(n)}为k阶平稳随机过程,则该过程的k阶矩定义为:

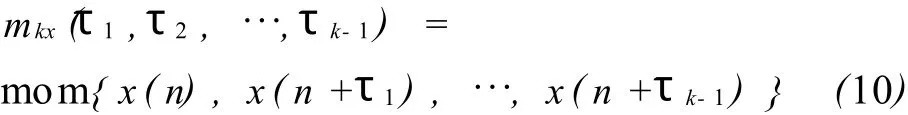
而k阶累积量定义为:

1.4 高斯过程的矩和累积量

根据定义,可以证明平稳高斯过程{x(n)}的矩和累积量为:

可见,高斯过程的高阶累积量恒等于零,即使对有色高斯过程也是这样.这是在信号处理中使用高阶累积量的主要动机之一.高阶矩不具备这一优点.

1.5 高阶矩谱和高阶累积量谱

由高阶矩和高阶累积量的多维Fourier变换定义高阶矩谱和高阶累积量谱.

定义:设 mkx(τ1, …,τk-1)绝对可和,即:

则k阶矩谱定义为k阶矩的k-1维Fourier变换,即:

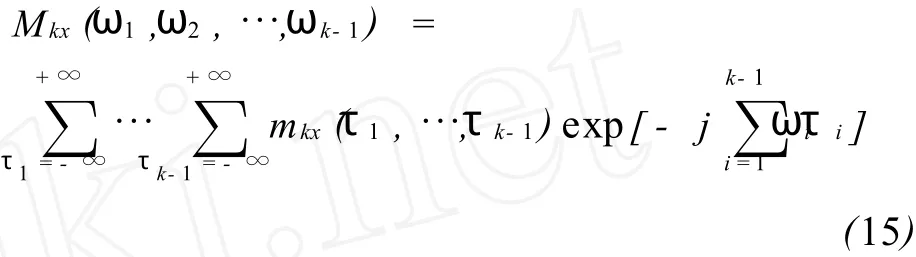
定义:设高阶累积量 ckx(τ1,…,τk-1) 绝对可和,即:

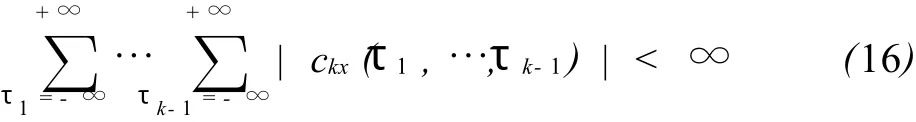
则k阶累积量谱定义为k阶累积量的k-1维Fourier变换,即:

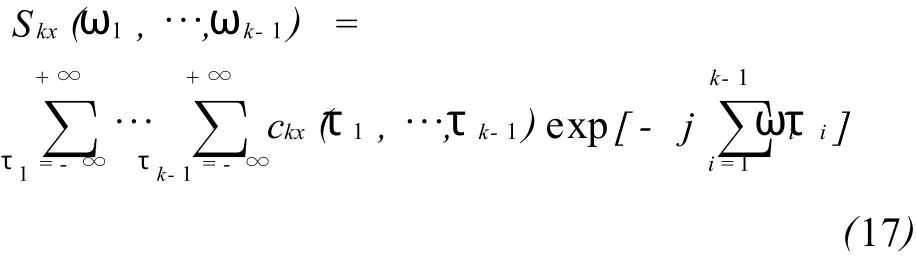
高阶累积量谱常简称为高阶谱或多谱(Polyspectra).最常用的高阶谱是三阶谱(双谱,Bispectrum):

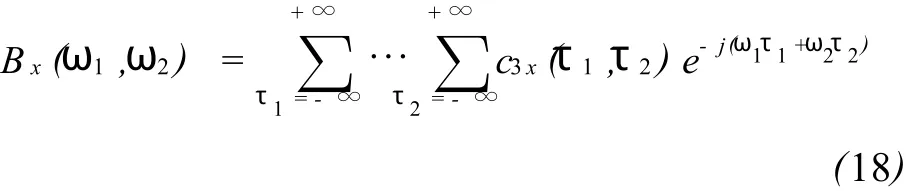
显然,对高斯随机过程,其双谱、三谱以及更高阶的谱恒等于零.考虑计算复杂性,实际中主要用到三、四阶累积量以及双谱和三谱.本文即用高斯随机过程双谱等于零的特点来检测信号.

2 微弱信号的双谱估计

考虑如下二元问题:

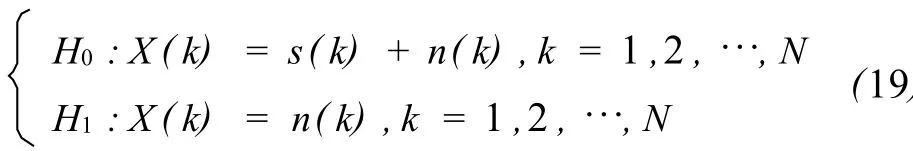
式中,s(k)为实信号,n(k)为高斯噪声,两者互不相关.对上述信号采用传统的估计方法,则有:

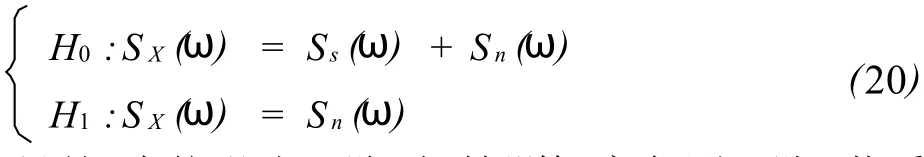
显然,当信噪比下降时,检测概率急剧下降,若采用双谱方法[11],则有:

因此,只要信号的双谱信息足够大,即使在信噪比很小的情况下,也能够获得较高的检测概率.

3 仿真结果

现假设信号为 x(n)=cos(2πf1+φ1)10e(n),其中 f1=0.10,φ1=π/2,e为零均值的高斯白噪声,我们用双谱估计信号信息.基于间接法双谱估计的仿真结果如图1-5所示.

由以上仿真图明显看出,由于高斯噪声的双谱为零,高斯噪声情况下微弱目标检测可以利用双谱技术检测出来.

4 结 语

高阶累积量与高阶累积量谱对于微弱信号的检测具有明显的优势,可以利用高斯噪声的双谱为零的特征,检测出混杂在噪声里的微弱信号.本文采用双谱分析方法,对强噪声背景下的微弱信号进行检测,仿真结果表明,该方法效果良好.

[1] 刘俊,张斌珍.微弱信号测技术[M].北京:电子工业出版社,2005:26-32.

[2] 王一清,宋爱国,黄惟一,等.一种用于混沌信号去噪的循环相关算法[J].仪器仪表学报,2005,26(4):403-406.

[3] 杜京义,侯媛彬.混沌背景中微弱谐波信号检测的SVM方法[J].仪器仪表学报,2007,28(3):555-559.

[4] 张威,王旭,葛琳琳,等.一种强噪声背景下的微弱信号检测的新方法[J].计量学报,2007,28(1):70-73.

[5] 戴桂平,刘彬.基于小波去噪和EMD的信号瞬时参数提取[J].计量学报,2007,28(2):158-162.

[6] 梁军利,杨树元,唐志峰.基于随机共振的微弱信号检测[J].电子与信息学报,2006,28(6):1068-1072.

[7] 邵菊花,李立萍.基于随机共振的不同非线性系统的微弱信号检测性能分析[J].电子对抗,2008(3):6-10.

[8] 赵吉祥,陈超婵,王欢,等.微弱电信号检测方法回顾[J].中国计量学院学报,2009,20(3):201-210.

[9] 王秉仁,杨艳霞.双谱分析在旋转机械故障诊断中的应用[J].煤矿机械,2009,30(1):215-217.

[10] 李宏伟,程乾生.高阶统计量与随机信号分析[M].北京:中国地质大学出版社,2002:1-57.

[11] 飞思科技产品研发中心.Matlab7辅助信号处理与应用[M].北京:电子工业出版社,2005:382-403.

The Application of Bi-spectrum in Weak Signal Test

WANG Feng-ge,WANG Hui,L IXiao-quan
(1.Zhongyuan University of Techno logy,Zhengzhou 450007;2.Zhengzhou University,Zhengzhou 450052,China)

For the bi-spectrum of Gaussian noise is zero,bi-spectrum analysis is used to detect weak signals in the background of strong noise.Simulation results show that themethod can well restrain noise and detect the useful signals.

higher-o rder cum ulants;higher-o rder cumulant spectrum;noise;detection

TN911.6

A DO I:10.3969/j.issn.1671-6906.2010.02.002

1671-6906(2010)02-0005-04

2010-03-19

国家自然科学基金项目(50977093)

王凤歌(1978-),女,河南伊川人,讲师,硕士.