一种基于改进阈值函数的小波图像去噪算法

刘洲峰,程 寅

(中原工学院,郑州 451191)

一种基于改进阈值函数的小波图像去噪算法

刘洲峰,程 寅

(中原工学院,郑州 451191)

在Dohono D L提出的多分辨分析小波阈值去噪算法的基础上,提出了一种新的阈值函数.与传统的硬阈值和软阈值比,此函数不仅易计算,而且具有优越的数学特性和清晰的物理意义.实验结果表明,该方法可有效地去除白噪声干扰,无论在视觉效果还是在信噪比和均方误差定量指标上均明显优于常用的软、硬阈值及改进的软硬阈值折中算法,充分体现出小波阈值去噪方法的优越性.

小波变换;图像去噪;阈值;阈值函数

在图像的采集过程中,常会受到随机噪声的干扰.噪声的存在,破坏了图像在结构等方面的相关性,不利于特征的提取.因此,在对图像进行后续的分析之前,一般都要对其进行去噪处理.传统的去噪方法仅具有空间域或频域的局部的分析能力,在抑制图像噪声的同时,损失了图像的边缘等细节信息,使处理后的图像变得模糊.小波分析在时域和频域同时具有良好的局部化特性,使它特别适合于图像的去噪.1995年,Donoho D L首次提出了小波阈值这个概念[1-3],由于此方法在Besov空间上可以得到最佳的估计值,而其他的线性估计都达不到与此相同的结果,因此引起了国内外学者的注意[4-6].

本文首先在Donoho提出的小波去噪的基础上,以加性高斯噪声为前提,根据噪声所占子带系数方差的比例对阈值进行了改进,并提出了一种新的阈值函数,该阈值函数高阶可导,是现有软、硬阈值函数的推广,而且通过调整参数,还可以克服硬阈值函数不连续和软阈值函数有偏差的缺点,同时具有能量自适应性.实验结果表明了该算法在均方误差意义上的最优性,并且可以保留图像的细节信息.

1 图像的小波变换

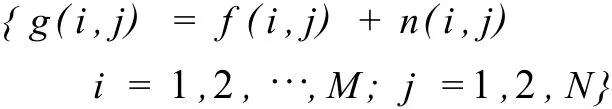
考虑含有噪声的图像模型:其中:f(i,j)是原图像(未含噪声);n(i,j)～N(0,σ2)且独立同分布,与 f(i,j)也是相互独立的;M×N为图像尺寸.

含噪图像 g(i,j)经小波变换后有Wg=Wf+Wn,其中Wg为含噪图像的小波系数,Wf为原图像的小波系数,Wn为噪声小波系数.

2 算法实现

2.1 小波变换阈值去噪

Donoho提出的小波阈值去噪法的基本思想是:当Wj,k小于某个临界阈值时,小波系数主要是由噪声引起的,予以舍弃;当Wj,k大于这个临界阈值时,小波系数主要是由信号引起的,那么就把这一部分的Wj,k直接保留下来(硬阈值方法),或者按某一个固定量向零收缩(软阈值方法),然后用新的小波系数进行小波重构得到去噪后的信号.

Donoho使用的硬阈值函数为:

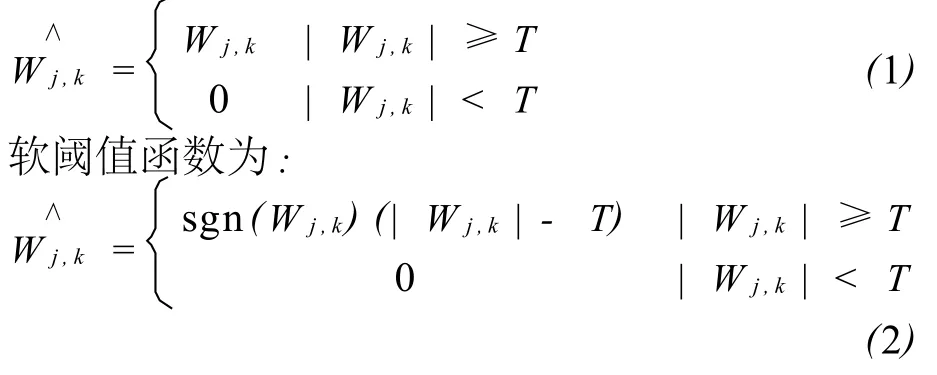
此方法可通过以下3个步骤实现:

(1)对含噪信号 f(k)作小波变换,得到一组小波系数Wj,k;

(2)通过对Wj,k进行阈值处理,得出估计小波系数Wj,k使得 ‖Wj,k-Uj,k‖尽量小;3)利用Wj,k进行小波重构,所得到的估计信号∧f(k),即为去噪后的信号.

在这3个步骤之中,最关键的是如何选取阈值和如何进行阈值量化[7],因为量化和选取目的是为了滤掉噪声的小波系数,保留原图像小波系数,因此它直接关系到图像去噪的质量.

2.2 阈值的选取

小波变换有3个主要的属性:局部性、多尺度性和压缩性.随着小波分解级数的增加,更多的信号能量集中在个别小波系数上,这就使得个别小波系数的幅值远远大于其他小波系数,如前所述,小波将噪声从信号域映射到了小波域,这就意味着噪声的方差并没有随着小波分解级数的变化而变大,而原始图像的小波分解系数的方差会变大.

为了研究噪声方差和小波分解高频子带系数方差的特点,我们加人了标准差为25的加性白高斯噪声在Lena图(512＊512)上,同时在像素点值全部为0的图像(黑图像)上叠加同样的噪声,然后做1～5级小波分解.实验结果如表1所示,σ2subband表示含噪声的Lena图 HH子带系数方差,σ2noise是黑图像上叠加噪声的HH子带系数方差.可以看出,含噪声图的第一级小波分解子带系数方差几乎等于噪声方差,这说明该子带所含信息几乎被噪声淹没.而随着分解级数的增加,噪声在系数方差中所占的比重越来越小,在第5级分解中仅为0.73%.

根据噪声所占子带系数方差的比例可以得知,我们不能在更高的小波分解级数中直接用Donoho的阈值法,而应该对这个阈值做一定的修改,使 T乘上一个比例系数,使它能随着小波分解级数的增加而变化.通过对表1的分析,我们希望这个比例系数在一、二级分解的时候近似为1,此时本文算法和Donoho的阈值一致,而到了第三级分以上近似于1/2～1/3.我们取 T=σ 2lg N/ln(e+j2-1).其中 N为信号长度,σ为噪声标准方差,j=0,…,J,J为小波分解级数.

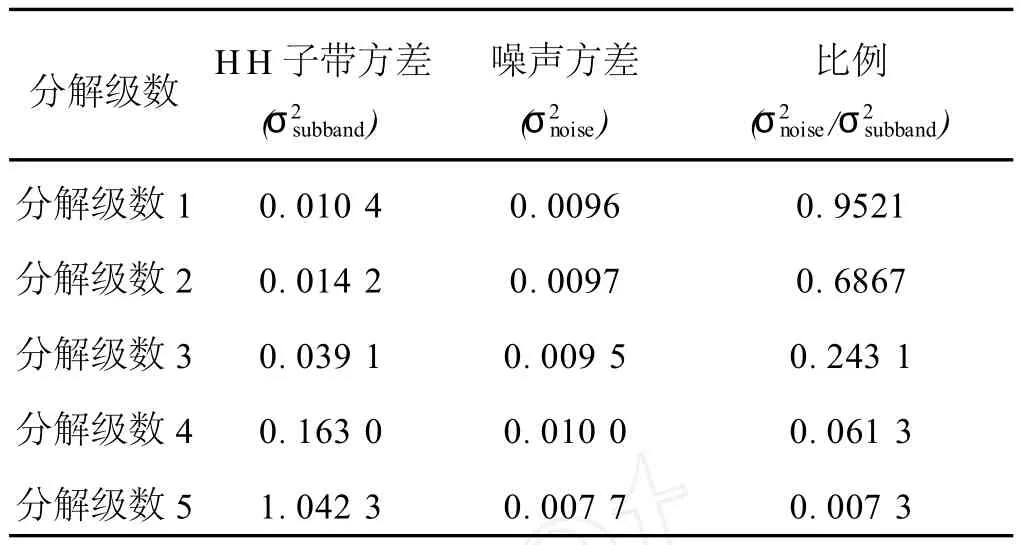
表1 各级小波分解系数(HH子带)方差和噪声方差及比值

2.3 一类新阈值函数的构造

硬、软阈值法虽然在实际中得到了广泛的应用,也取得了较好的效果,但这些算法本身存在着一些缺陷.在硬阈值方法中,处理过的小波系数 在 ±λ处是不连续的,在信号重构时,易产生Pseudo-Gibbs现象;而经过软阈值方法处理过的小波系数虽然整体连

∧续性较好,但Wj,k与Wj,k间总存在恒定的偏差,这将直接影响重构图像与真实图像的逼近程度,给重构图像带来不可避免的误差.但是若把这种偏差减小到零(硬阈值情况),也未必是最好的.为此构造了一类新的阈值函数

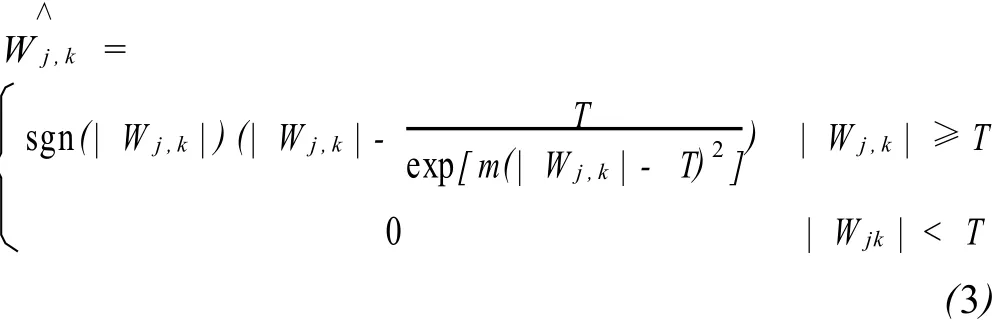
式中,m≥0为阈值.该函数不仅在小波域内具有与软阈值函数相同的连续性,而且在|Wj,k|≥T时有高阶导函数.当m→0时,式(3)可以看作是软阈值函数,当m→∞时,式(3)可以看作硬阈值函数.所以,该函数是现有软、硬阈值函数的一种推广,通过调整参数,可以克服硬阈值函数不连续和软阈值函数有偏差的缺点,同时具有能量自适应性.

考虑函数:

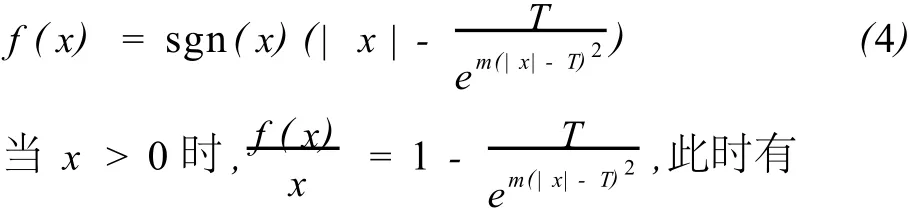
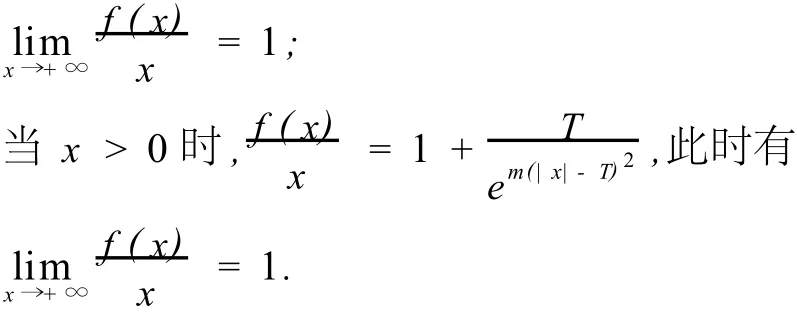
所以,新阈值函数是以直线y=x为渐近线的,它克服了软阈值函数估计值与原始值之间具有恒定偏差的缺点.

3 评价体系的建立

在计算机内存中,图像是以矩阵的形式被存储的.鉴于这一特点,我们可以建立评价不同去噪方法优劣的标准.

一个是图像的均方误差M SE,其定义为:

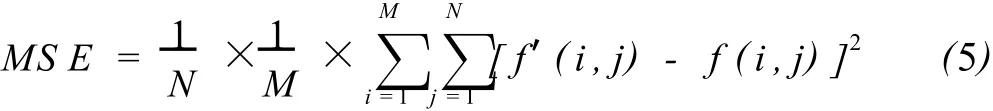
式中:M×N为图像矩阵的大小;f′(i,j)为小波变换后的图像在(i,j)位置处的像素值;f(i,j)为原始图像在(i,j)位置处的像素值;2个求和符号表示对图像矩阵中的元素进行遍历.

另一个是图像的峰值信噪比PSNR,其定义为:

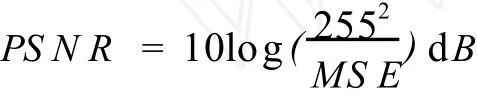
4 实验结果与分析

本文选用db8小波基对图像进行分解.db8小波基支集长度长,消失矩和正则性高.消失矩阶数大,小波能量集中,正则性好,则二维图像重构后就越平滑.本文对各种灰度图在不同噪声水平(σ=20,25,30)下进行了仿真实验[8],我们以含噪 Lena图(大小为256＊256,灰度级为256)为例进行说明.实验结果如图1所示.

另外采用峰值信噪比和均方误差对去噪图像进行定量分析比较,定量分析结果如表2所示.

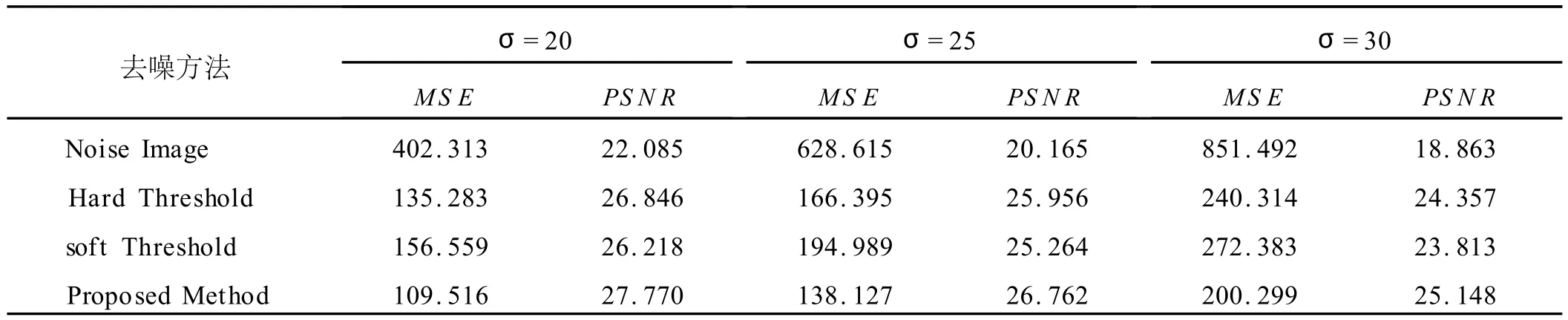
表2 不同图像去噪方法均方误差和峰值信噪比

从图1中可以看出,新阈值函数图像在视觉效果上要优于软阈值函数和硬阈值函数,表2定量地描述了这种优越性;同时,我们提出的新阈值函数不仅有效地去除了一定的高斯噪声,而且比较好地保留了图像的边缘信息,改善了图像的峰值信噪比.

5 结 语

本文主要介绍了小波阈值去噪的基本理论和算法,并且阐述了阈值、阈值函数的选择问题.在此基础上提出了一种新的阈值函数.该新阈值函数是现有软、硬阈值函数的推广,通过调整参数,可以克服硬阈值函数不连续和软阈值函数有偏差的缺点,同时还可以表达出分解后的小波系数的能量分布.经实验验证,本文所提出的阈值函数不仅可以有效地去除噪声,还可以保留图像的细节信息,同时在视觉上有更好的效果.

[1] Donoho D L.De-noising by Soft-thresholding[J].IEEE Trans.Info rm.Theo ry,1995,41(3):613-627.

[2] Donoho D L,Johnstone IM.Ideal Spatial Adap tation via Wavelet H rinkage[J].Biometrika,1994,81(12):425-455.

[3] Donoho D L,Johnstone IM.Adap ting to Unknow n Smoothness Via Wavelet Shrinkage[J].Jounalof the American Statistical Assoc,1995,90(432):1200-1224.

[4] ZHANG Xiao-ping,Desai M D.Adap tive Denoising Based on SURE Risk[J].IEEE Signal Processing Letters,1998,5(10):265-267.

[5] CHANG S Grace,YU Bin,L IM Vattere.Adap tive Wavelet Thresholding for Image Denoising and Comp ression[J].IEEE Trans.Image Processing,2000,9(9):l532-1546.

[6] CHANG SGrace,YU Bin,L IM Vattere.Spatially Adap tive Wavelet Thresholding w ith Context Modeling for Image Denoising[J].IEEE Trans.Image Processing,2000,9(9):1522-1530.

[7] 李庆武,陈小刚.小波阈值去噪的一种改进方法[J].光学技术,2006,32(6):831-833.

[8] 高成.Matlab小波分析及其应用[M].北京:国防工业出版社,2007.

AWavelet Image Denoising Method Based on Improved Threshold Function

L IU Zhou-feng,CHENG Yin
(Zhongyuan U niversity of Technology,Zhengzhou 450007,China)

Based on the M ulti-analysiswavelet threshold denosing method w hich put fo rward by Dohono,a new threshold function is p roposed.This new thresholding function has many advantages over the classical soft and hard thresholdding function.It is clear in physicsmeaning and simp le in exp ression.The results show that this imp roved method is effective in removing w hite noise.and gives better RM SE performance and SNR gains than the soft and hard thresholdingmethodsand embadies the advantagesof thewavelet threshold denoising method mo re fully.

wavelet transform;image denoising;threshold;threshold function

TP391

A DO I:10.3969/j.issn.1671-6906.2010.02.011

1671-6906(2010)02-0042-04

2010-03-16

河南省教育厅自然科学基金项目(200410465201;200510465002)

刘洲峰(1962-)男,河南新乡人,教授,博士.