缓冲材料振动传递率的测试及非线性辨识*

周 健 张 丽 王保升

南京工程学院 江苏南京 211167

缓冲材料振动传递率的测试及非线性辨识*

周 健 张 丽 王保升

南京工程学院 江苏南京 211167

本文依据相关的标准和工程实际需求，分析了振动传递率测试中的试样固定方式，设计了一种简易固定装置。以发泡聚乙烯为例，分析了振动传递率测试方法，将4种厚度规格的试样分别在5种应力下进行了3Hz～200Hz的扫频试验，测出了发泡聚乙烯在不同厚度和应力下的振动传递率，并对试验结果进行了分析。采用BP神经网络建立了振动传递率非线性模型，并利用matlab/nntool对网络进行了训练和仿真，结果表明，该模型具有较强的泛化能力，能精确辨识振动传递率，从而可以预测任意厚度和应力下的振动传递率。

缓冲材料；振动传递率；测试；非线性辨识

目前，保护产品在流通过程中免遭冲击、振动等机械载荷损坏的有效常用方法，是在包装中添加缓冲材料。缓冲材料可以大量吸收能量，起到隔振作用，避免内装物因冲击、振动引起损伤。缓冲衬垫能否满足防振的要求，需要通过防振校核和振动试验来验证。缓冲材料振动传递率的确定是防振校核过程中一个重要的步骤，测试的精确度决定着校核的准确性。在缓冲和防振设计中，一般是在完成缓冲设计后，确定衬垫材料、衬垫厚度以及衬垫所受到的静应力，然后进行扫频振动试验测试振动传递率，实现振动校核，每次设计都需要做相应的振动试验获得振动传递率。虽然，国内外不少研究人员在包装材料振动传递率方面做了大量的工作，但只是针对某一种或一类材料进行的，并且只是针对规格化应力和厚度进行试验得出一些性能曲线，对于规格化以外的并未给出判断的方法，只能重新试验。而缓冲材料大多表现出较强的非线性，很难通过解释公式计算。

本文通过自行设计一种简易固定装置，对常用缓冲材料在一定应力和厚度下的振动传递率进行了测试。利用神经网络在非线性函数逼近方面的优越性，建立缓冲材料振动传递率的神经网络模型，将其线性和非线性作为一个整体来识别，利用所建立的模型及辨识结果代替原来的传递率曲线，从而可以对缓冲材料在任意应力和任意厚度下的振动传递率进行预测，为防振设计提供基本数据。

一、简易固定装置设计

依据国家标准GB/T8169-2008(包装用缓冲材料振动传递率特性试验方法)，结合包装件在实际流通过程的装载方式，设计了如图1所示的固定方式。图中，材料1、材料2为同一种材料，具有相同的厚度，即为待测的试样。固定装置的作用为模拟包装容器(主要是模拟容器的上壁和下壁)，由于包装容器的内高在运输过程中不会改变，因此，固定装置需采用刚性材料。

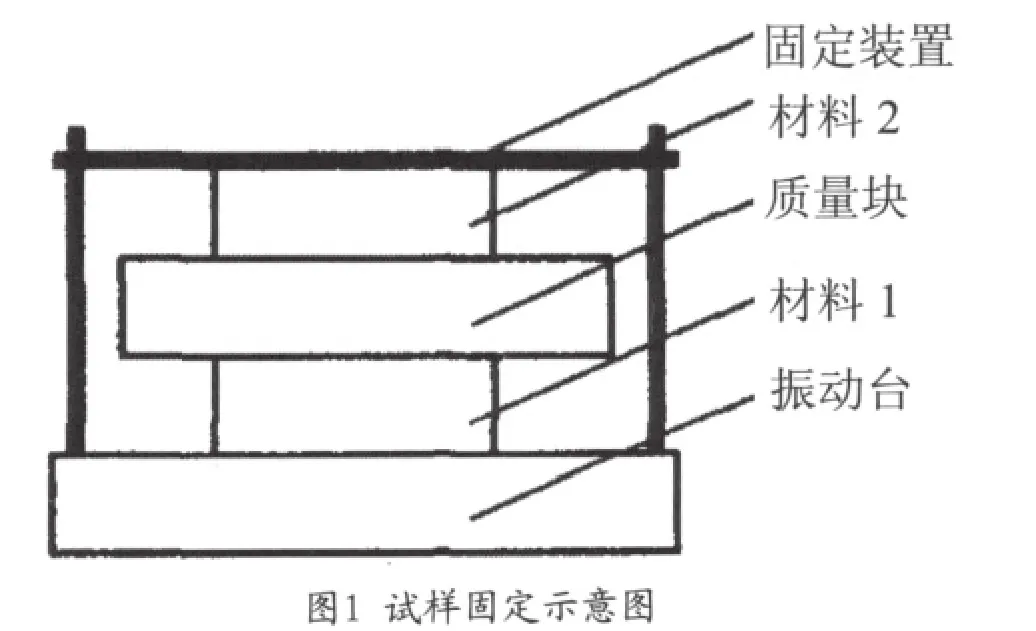
依据固定要求，本文设计了一种简易固定装置(如图2所示)。利用4根螺杆支撑固定板，在固定板的上下两面利用螺母与螺杆固定住。标准中要求固定板对实验材料的应力为0.7kPa，本装置中的固定板重量为2.8kg，当压在20cm×20cm的试样上，产生的应力正好为0.7kPa，只要将压板平放在缓冲材料上，然后用螺母上下固定即可，该装置操作简单，满足实验要求，也便于固定高度的调节。

图2 简易固定装置

二、振动传递率测试

1.试验材料及设备

试验材料为密度0.032g/cm3的发泡聚乙烯EPE(厚度分别为2.5cm、5cm、7.5cm、10cm)，试样尺寸为20cm×20cm。振动试验系统为DC-600(苏州实验仪器总厂)，该系统由DC-600振动台、RC-2000振动控制仪、控制计算机、CA-YD-185加速度传感器、电荷放大器、FJ-1000鼓风机、开关式功率放大器、质量块及固定装置等构成。加速度数据采集与分析使用DH5920动态信号测试分析系统(江苏东华测试技术有限公司生产)。试验设备的连接如图3所示。

图3 试验设备连接示意图

2.试验方法

试样固定方式：按图1和图2所示固定。

振动参数设置：频率为3Hz～200Hz；扫频速率为0.5oct/min；激振方式采用恒定加速度，大小为1g；扫频次数为1次。

试验方案：对2.5cm，5cm、7.5cm和10cm厚的EPE分别在0.7kPa、1.26kPa、1.477kPa、1.75kPa、2.198kPa的静应力下的振动传递率进行测试。

3.结果与分析

按照上述试验方法，加速度传感器2、3对应的通道分别显示一条振动传递率曲线，由于曲线不便于求平均值，本试验通过导出曲线对应的Excell文件，然后取6个点对应的两者平均值来代替整个振动传递率曲线。20组试验的结果如表1所示。利用表1中的数据即可拟合出对应的振动传递率曲线，图4为厚度为2.5cm的EPE在0.7kPa时的振动传递率曲线。

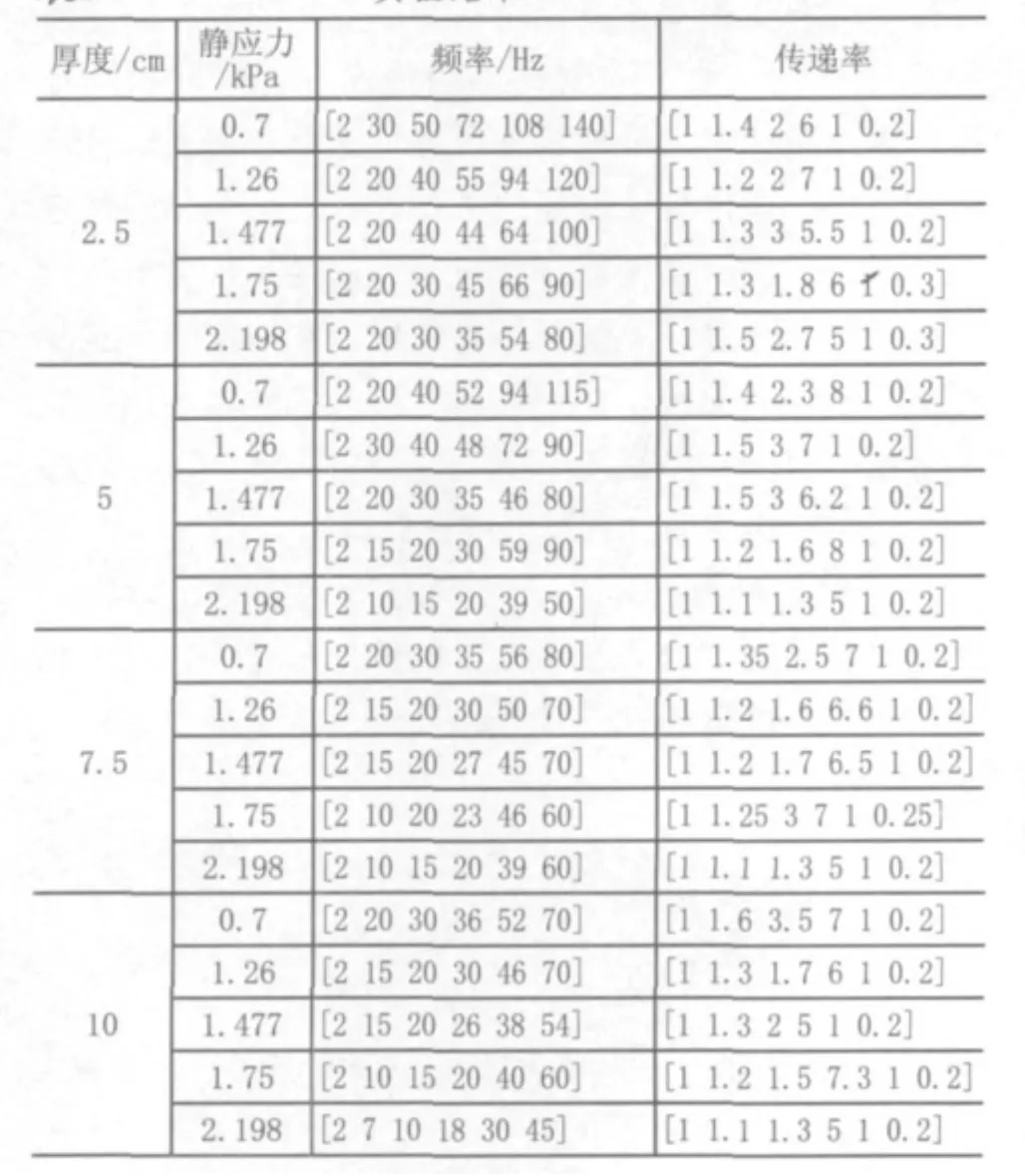
表1 实验结果

由试验结果可以得出以下结论：

(1)当激振频率较小时，传递率接近于1(大于1)；当质量块发生共振时(即激振频率等于系统的固有频率)振动传递率达到最大值；随着激励频率的进一步增大，振动传递率减小，当达到某一频率后，振动传递率小于1，为减振区(见图4)。

(2)应力和厚度的增大，均使最大传递率对应的频率减小，说明系统的固有频率随着应力和厚度增大而减小。但最大传递率的变化不具有明显的特征，这可能是由材料内部的粘性阻尼以及试验精度造成的。

三、振动传递率的非线性辨识

利用振动传递率曲线只能通过人工读取所需要的传递率数值，存在较大误差，并且如果没有相符的振动传递率曲线，必须进行测试。由于缓冲材料的振动传递率具有较强的非线性特点，很难利用解析式计算任意厚度任意应力下的振动传递率。本文利用BP神经网络可以逼近任意非线性函数的优点，依据实际应用，建立两种振动传递率的神经网络模型对振动传递率进行辨识。

1.BP神经网络概述

BP网络是一种单向传播的具有3层或3层以上的神经网络，包括输入层、中间层(隐层)和输出层(如图5所示)。层之间实现全连接，而每层神经元之间无连接。当一对学习样本提供给网络后，神经元的激活值从输入层经各中间层向输出层传播，在输出层的各神经元获得网络的输入响应。接下来按照减少目标输出与实际误差的方向，从输出层经过各中间层逐层修正各连接权值，最后回到输入层，这种算法称为“误差逆传播算法”，即BP算法。当神经网络的训练结束后，网络就依据学习样本实现输入输出影射关系。此时，给定不是样本集中的输入，网络也能给出合适的输出。网络模型，结构如图6所示，T、为网络输入，Tr与 f为网络输出。

图5 神经网络模型

2.最大传递率的辨识

(1)神经网络模型

在实际应用中，最大传递率是非常重要的指标，有些应用情况下，设计人员只关心最大振动传递率的数值以及对应的频率。当材料一定时，影响最大传递率的因素为厚度和应力。因此，本文建立两输入两输出的神经网络模型，其隐层节点数取6，即2-6-2神经

图6 振动传递率模型

(2)网络训练及仿真

根据以上所给出的模型，做如下设置：

①学习样本的个数N设为19个，样本输入、输出为表1中的数据，输入为：[2.5 2.5 2.5 2.5 2.5 5 5 5 5 7.5 7.5 7.5 7.5 7.5 10 10 10 10 10; 0.7 1.26 1.477 1.75 2.198 0.7 1.26 1.75 2.198 0.7 1.26 1.477 1.75 2.198 0.7 1.26 1.477 1.75 2.198]，输出为：[6 7 5.5 6 5 8 7 8 5 7 6.6 6.5 7 5 7 6 5 7.3 5; 72 55 44 45 35 52 48 30 20 35 30 27 23 20 36 30 26 20 18]。

②训练函数为TRAINGDA，自适应学习函数为LEARNGDM，误差性能函数为MSE。

③学习误差小于0.1或学习次数大于100000次时退出程序。

依据设置的参数，利用matlab中的神经网络工具箱(nntool)对网络模型进行训练，初始权值和阈值采用随机值。当网络训练次数达到1589次训练结束，全局误差为9.94056e-2。训练后输入层到隐层权值和阈值分别为[0.9834 -6.707；3.891 3.476；2.3952 -2.9579；4.152 8.8397；-2.1923 7.654；2.599 -8.1504]和[-5.017；-18.42；-7.4138；-14.8492；-14.511；7.3704]。隐层到输出层权值和阈值分别为：[2.5979 0.55345 2.309 6.1338 -3.7895 2.2963；-2.1189 4.5701 -2.4392 3.7833 -2.3976 2.7415]和[-2.6791；1.6316]。

为验证模型的泛化能力，以测试样本的厚度5cm和应力1.477kPa作为模型的输入，模型的输出值为Tr=5.84，f=38。与样本中的Tr＝6.2，f=35比较接近，其误差分别为5.8%和8.6%，这说明该模型能较为精确的预测最大振动传递率。

3.任意频率对应的传递率辨识

当需要预测一定厚度、一定应力下，某一激振频率所对应的振动传递率时，无法用图6所示的模型实现，需另外建立一种新的模型。此情况下，决定振动传递率的因素有厚度T、应力和频率f，而输出只有振动传递率Tr，因此该模型有3个输入和1个输出。取10个隐层节点，模型与图6类似，只是各层的节点个数不同。取表1中的部分数据作为训练样本即可对网络进行训练和仿真，过程与上述方法类似，其结果仍能对振动传递率进行较为精确的预测。限于篇幅问题，在此不再赘述。

四、结束语

本文依据流通过程中的实际情况和有关国家标准，设计了一种简易方便的固定装置。依据影响振动传递率的因素，对缓冲材料在不同情况下的振动传递率曲线进行了测试，便于以后的使用。为减少试验次数，对不同情况下振动传递率的神经网络预测方法进行了研究，计算机模拟结果表明，该方法对于振动传递率的非线性辨识是有效的，辨识结果可以较精确的预测振动传递率。虽然本文仅以EPE材料为例进行研究，但对于其它材料的非线性辨识同样适用，文中的工作为今后缓冲材料振动传递率的进一步研究提供了基础。

[1]马伟伟,钱静.振动传递率在优化防振设计中的应用[J].包装与食品机械,2008,26(2):19～22

[2]彭国勋.物流运输包装设计[M].北京：印刷工业出版社，2006

[3]杨晓伟，梁艳春，龚文英，等.包装件非线性特性识别的进化神经网络混合方法[J].吉林工业大学自然科学学报，2001,31(1)：66～70

[4]黄雪. GB/T 8169-2008包装用缓冲材料振动传递率测试方法[M].北京：中国标准出版社，2008

[5]周开利，康耀红.神经网络模型及其matlab仿真程序设计[M].北京：清华大学出版社，2005

Testing and nonlinear identif cation of vibration transmissibility for cushioning materials

Zhou Jian, Zhang Li, Wang Baosheng
Nanjing institute of technology, Nanjing, 211167,China

Basic relevant standards and engineering demand the sample fixed method was analyzed, a simple device was designed. Test method of vibration transmissibility taking expanded polyethylene for instant was analyzed. The samples were divided into four kind of thickness, and a series of vibration transmissibility was tested through frequency scanning test from 3-200Hz with deferent stress. The results were analyzed. A nonlinear model for vibration transmissibility was established with BP network, trained and simulated with matlab/nntool. The results show that the model has a better generalization and identification ability, and can be used to predict the vibration transmissibility of cushion materials with different thickness and stress.

cushioning materials; vibration transmissibility; testing; nonlinear identification

2009-11-23

周健，在读本科生。张丽，本科，讲师。王保升，硕士，讲师。通讯作者：王保升。

*本文系南京工程学院科研项目KXJ08058，南京工程学院大学生创新项目N20080203。