Lap lace变换的应用研究

姜立新

(德州职业技术学院,山东德州 253034)

Lap lace变换的应用研究

姜立新

(德州职业技术学院,山东德州 253034)

利用Lap lace(逆)变换及其具有的积分性质、微分性质、卷积性质,来求解一些特殊类型的无穷积分,并讨论了Lap lace变换在求解微分方程(组)、积分方程中的应用.

拉氏变换;无穷积分;微分方程;积分方程＊

0 引言

Lap lace变换属于积分变换的一种,它是通过积分运算把一个函数变成另一个函数的变换,它将函数的微积分运算转化为代数运算,在力学、电学、控制论等工程技术与科学领域中有着广泛的应用.

1 预备知识

引理1 (拉普拉斯变换存在定理)[1～3] 如果函数f(t)满足下面两个条件:(1)在t≥0的任一有限区间上分段连续;(2)存在常数M>0及c≥0,使得f(t)≤M ect(0≤t<+∞)成立;那么,f(t)的拉普拉斯变换F(s)=f(t)e-std t在半平面R e(s)>c内一定存在,且是解析的.

符号说明:Y(s)=L[y(t)],X(s)=L[x(t)]

2 利用Lap lace变换求解无穷积分

分析:由拉氏变换像函数的积分性质知:若F(s)=L[f(t)]且d t收敛,则

3 求解微分方程(组)初值问题

例4 求微分方程y″-3y′+2 y=2e-t,满足初始条件y(0)=2,y′(0)=-1的特解.

解:设L[y(t)]=Y(s),对微分方程两端取拉氏变换得

[s2Y(s)-sy(s)-y′(s)]-3[sY(s)-y(0)]+2Y(s)=,考虑到初始条件得

(s2-3 s+2)Y(s)=+2p-7,于是

对上述方程两边取拉氏逆变换,得

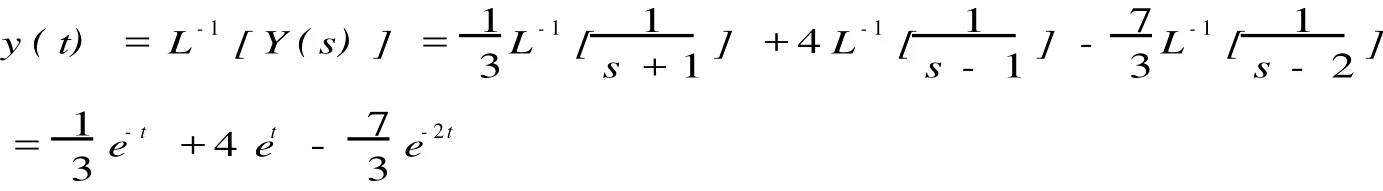
解:设L[y(t)]=Y(s),L[x(t)]=X(s),对微分方程组两端取拉氏变换得

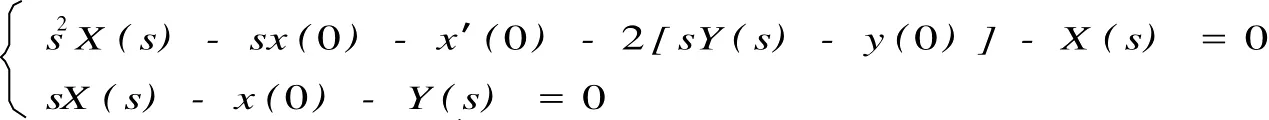
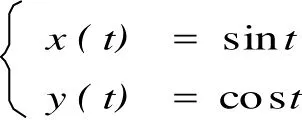
例6 求变系数微分方程ty″+2(t-1)y′+(t-2)y=0,满足初始条件y(0)=0的解

解 方程两边同时实施拉氏变换,利用拉氏变换的微分性质有

结合初始条件y(0)=0,化简有

(s2+2s+1)Y′(s)+4(s+1)Y(s)=0,解之有

所以y(t)=L-1[Y(s)]=C t3e-t

4 求解积分方程

对积分方程两边同时实施拉氏变换并由卷积定理得

故

两边取拉氏逆变换得

所以,y(t)=L-1[Y(s)]=2-co s t-3 sin t

从以上几个例子可以看出,用拉氏变换求解相关问题既方便又简洁,但任何变换都有它的局限性,利用L ap lace变换时必须满足它的存在定理.

[1]张元林.积分变换(第四版)[M].北京:高等教育出版社,2003.

[2]白艳萍,雷英杰,扬明.复变函数与积分变换[M].北京:国防工业出版社,2004.

[3]华中科技大学数学系.复变函数与积分变换(第二版)[M].北京:高等教育出版社,2003.

[4]钱学明.利用拉普拉斯变换求解几个重要的广义积分[J].河北北方学院学报(自然科学版),2008,24(3):4-7.

[5]施晓红.Lap iace变换在求解线性微分及积分方程中的应用[J].昆明理工大学学报(理工版),2009,34(3):121-124

Abstract:Based on the concepts and the properties of Lap lace transformation,this paper solves some special types of infinite integral and discusses its applications in solving problems of differential equation with coefficients,solving integral eqution.

Keywords:Lap lace transformation;infinite integral;differential eqution;integral eqution

Application Research of The Lap lace Transformation

JIANG L i-xin
(De Zhou Vocational and Technical College,De zhou 253034,China)

O177.6

A

1004-7077(2010)02-0037-04

2010-01-23

姜立新(1966-),女,山东省宁津县人,德州职业技术学院副教授,理学硕士,研究方向为数学物理方程.

[责任编辑:陈庆朋]