指数平滑法及其在负荷预测中的应用
2010-10-22吉培荣
陈 娟 吉培荣 卢 丰
(1.三峡大学电气与新能源学院,湖北 宜昌 443002;2.荆州供电公司,湖北荆州 434023)
电力系统负荷预测是电力系统自动化领域中的一项重要内容,对于电力系统的控制、运行和规划都有着非凡的意义[1-2].
电力系统负荷预测理论和方法随时代的发展而进步,如今在深度和广度上都有了长足的进步.负荷预测总的来说可分为非数学和数学方法两大类.非数学方法有国际比较法、专家估计法等,数学方法主要包括相关法和外推法两类.相关法有回归分析法和投入产出法;外推法有指数平滑法、时间序列法、卡尔曼滤波法等.
指数平滑法作为外推法中的一种重要类型,运用尤为普遍.原因在于这种方法建立的模型较简单,计算简便、需要存贮的数据少,通过近期的观察值能很快地计算出新的预测值.在电力负荷预测方面,它既可用于对未来周日以小时负荷为统计样本的短期预测中,也可应用于中长期负荷预测中.负荷预测中,多运用指数平滑法中的线性模型和二次曲线模型.
指数平滑法模型的建立主要取决于历史数据的各次平滑值,而平滑值的变化制约于平滑系数α的大小,因此平滑系数α的取值很大程度上决定了预测的准确度.在过去的工作中人们选择α确定目标函数时对不同时间的模型误差同等对待,但实际上近年数据误差比远年数据误差对未来预测精度的影响更大,因此在优选α时对模型误差采用一视同仁的方式是不适合的.
本文采用厚近薄远原则确定目标函数,通过试验方法研究了用厚近薄远原则确定目标函数优选α对预测结果所造成的影响,直观证明了采用厚近薄远原则优选α的优越性,并对厚近薄远的程度问题进行了进一步的探讨.
1 指数平滑法介绍
1.1 指数平滑法基本原理
指数平滑法的一般公式是:
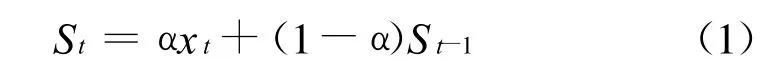
式中,St为第t期的平滑值;xt为第t期的实际观察值;St-1为第t-1期的平滑值;α为平滑常数,其取值范围为(0,1);将 St-1=α xt-1+(1-α)St-2,St-2=α xt-1+(1-α)St-3,St-3=α xt-1+(1-α)St-4 … …代入公式(1)可得:
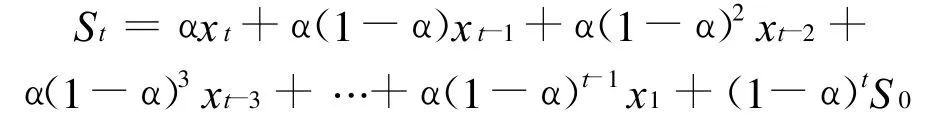
上述公式中各项系数和为
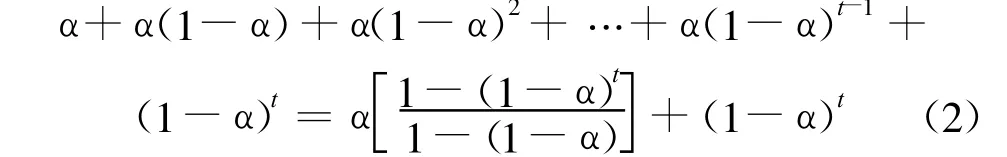
当t→∞时,(1-α)t→0,系数和→1,因此可以说St是t期及以前各期观察值的指数加权平均数,离t期越远,各期的数据的系数就越小,所对预测值产生的影响也越小.
公式(1)也可直接变换为

从上式中不难看出简单指数平滑法用于预测时实际上是根据本期预测误差对本期预测值作出一定的修正后得到的新的预测值,即:新的预测值=老预测值+α×老预测值的误差.
1.2 指数平滑法预测模型
指数平滑法有许多具体的模型,在实际负荷预报中使用的模型一般为线性模型和二次曲线模型.
1.2.1 线性模型
用于线性趋势预测的指数平滑方法的预测模型为
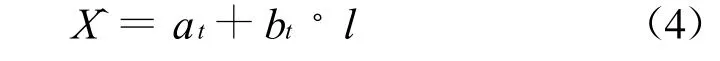

上式中,S(1)t、S(2)t分别为t期的一次平滑值、二次平滑值.
1.2.2 二次曲线模型
二次曲线模型是非线性预测,具体预测公式为
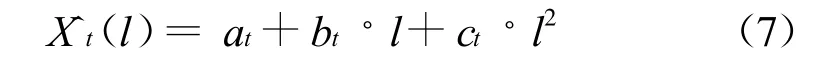
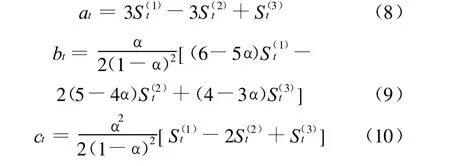
以上各式中,S(1)t、S(2)t、S(3)t分别为t期的一次平滑值、二次平滑值、三次平滑值.各次平滑值计算公式为:

以上各式中,Xt为t期的观察值,S(1)t、S(1)t-1分别为t期、t-1期的一次平滑值,S(2)t 、S(2)t-1分别为t期、t-1期的二次平滑值,S(3)t、S(3)t-1分别为t期、t-1期的三次平滑值.
2 优选平滑系数的原则和方法
平滑系数α的取值对平滑效果影响很大,常用的确定α的方法有公式估算法、经验法、试凑法(优选法)等.
2.1 搜索最佳α值的通用判据公式
用优选法搜索最佳α值采用的目标函数是模型误差,常用的模型误差有:

以上4个公式都有一个共同点,即把各期的模型误差不分远近同等看待,但实际上,近期的误差对预测的影响比远期的误差要大.应该这样说,衡量外推预测误差大小的判据与衡量曲线的拟合程度,判据应该有所不同,后者可对各期的绝对误差值采用等权的算术平均计算,而前者宜采用“厚近薄远”的加权算术平均[3],“厚近薄远”可以体现近期误差比较重要的特点.
2.2 采用“厚近薄远”原则优选α值时权重大小及判据公式的选择
“厚近薄远”原则的物理意义是,物理量未来的变化趋势更多地取决于历史时段中近期的发展规律,远期的历史数据与未来发展趋势的相关性较弱[4].
“厚近薄远”的具体做法有多种,本文采用的方法如下:给定一个β(0<β<1),将模型误差用下列各式确定:

2.3 搜索最佳α的方法
搜索最佳α的方法可采用0.618法[5-6],虽速度较快,但编程较复杂.本文采取等分法进行搜索.
在设ε=0.01的情况下,进行99次的运算选出最优的平滑系数,具体步骤如下:
设 ε=0.01,将 αi∈(0,1),i=1,2,3,…,99 分成100 个相同距离的区间,设 α1=0.01,α2=0.02,α3=0.03,…,α99=0.099.
(1)取 α1=0.01,将 α1代入公式(7)、公式(17)和公式(21),求出相对应的 MAPE(α1),WMAPE(α1);
(2)取 α2=0.02,将 α2代入公式(7)、公式(17)和公式(21),求出相对应的 MAPE(α2),WMAPE(α2);
……
(3)求出所有的 αi对应的 MAPE(αi)和WMAPE(αi)后,选择最小的 MAPE(αi)所对应的 αi值,这个值就是在远近相同原则下求出的最优α值;选择最小的 WMAPE(αi*)所对应的αi*值,这个值就是在厚近薄远原则下求出的最优α值.
(4)输出αi*以及 αi,到此整个优选过程结束.
该优选过程的流程图如图1所示.
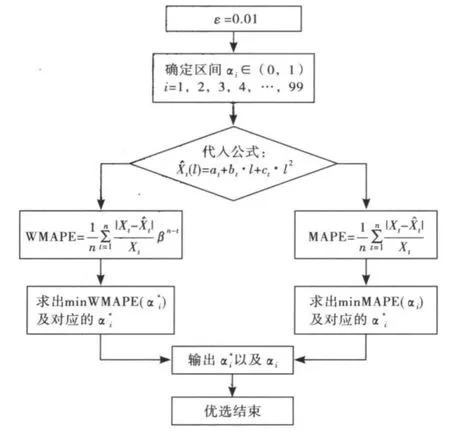
图1 优选过程的流程图
3 实验研究
以下6组数据分别为确定性数据(数据[1])、有随机偏差数据(数据[2]-[4])和实际年度负荷数据(数据[5]-[6]).
数据[1]:10,10.5,11,11.5,12,12.5,13,13.5,14,14.5,15,15.5.
数据[2]:6,14,16,24,26,34,36,44,46,54,56,64.
数据[3]:1,2,9,11,24,28,46,54,76,88,114,130.
数据[4]:2,6,10,8,15,25,31,49,67,86,97,95.
数据[5]:10.2,14.3,17.6,21.4,26.9,27.7,28.9,30.4,32.1,35.7,39.9,45.2(河南省某市1992~2003年用电量数据).
数据[6]:142.879,164.962,187.018,223.645,259.477,279.949,299.731,320.195,353.370,401.515,439.186,496.839(福建省1991~2002年全社会用电量数据).
实验过程中,分别采用MAPE和WMAPE作为优选平滑系数α的目标函数.实验程序用Delphi语言编制,用前11个(年)的数据按照远近相同原则和厚近薄远的原则优选出的平滑系数α值,见表1.从表1可以看出,对于确定性的数据,建模时采用远近相同原则和厚近薄远的原则优选出的α值是一样的;而对非确定性的数据,总体上看两种原则优选出的平滑系数是不一样的.对非确定性的数据,当β≥0.95时,采用远近相同原则和厚近薄远的原则优选出的平滑系数值是一样的;当β≤0.9时,两种原则优选出的平滑系数有差别,从β=0.85开始差别较明显,β愈小,差别愈大.
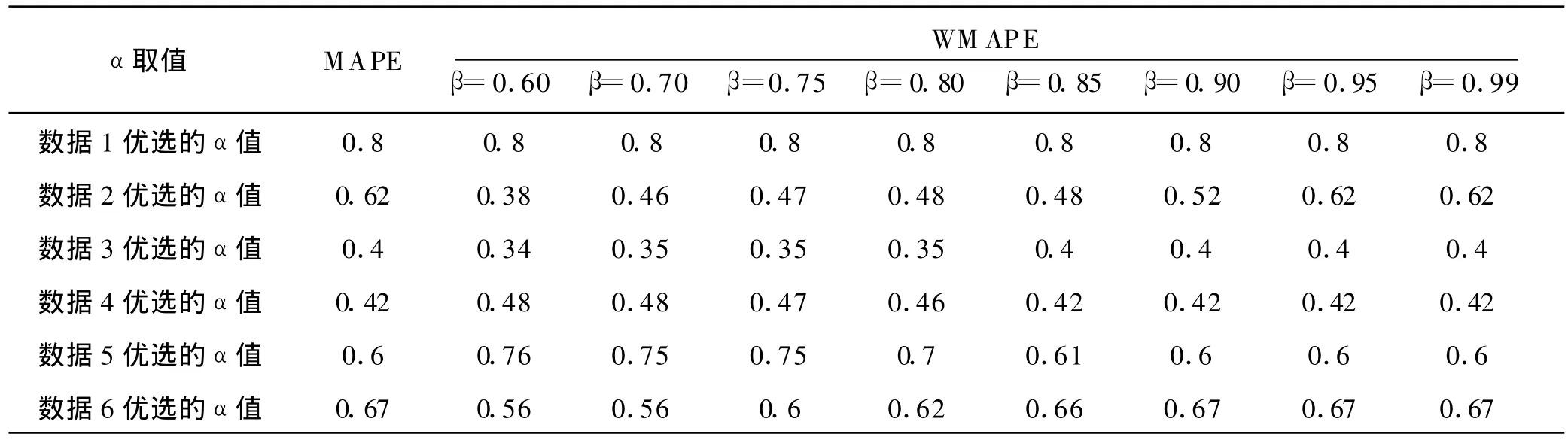
表1 按照远近相同和厚近薄远的原则优选出的平滑系数α值
从表1数据3~数据6的实验结果可以看出,β取值为0.8或0.85时,采用远近相同原则和厚近薄远的原则优选出的α值有比较大的区别,考虑到厚近薄远程度不适合太大,否则较远的数据几乎不起作用,因此厚近薄远推荐β取值为0.8左右.
下面取β=0.8时,用数据5、6对远近相同原则和厚近薄远原则优选出的α值对应的预测结果进行比较,见表2.

表2 按照远近相同原则和厚近薄远原则优选的α值及预测值比较
从上表可见,利用厚近薄远原则优选出的α值构成的模型预测精度较采用远近相同原则得到的模型预测精度要高,可见,采用厚近薄远的原则有实际意义.
4 应用实例
上海市1996~2007年用电量数据(摘自《上海统计年鉴》),见表3.

表3 上海市 1996~2007年用电量数据(单位:亿kW·h)
用1996~2006共11年数据建立二次曲线模型,采用远近相同的原则求出的最佳 α值为0.43,采用厚近薄远原则(β=0.8)求出的最佳α值为0.45.对这两个α值所对应模型求出的预测值与2007年的实际值进行比较,结果见表4.

表4 按照远近相同原则和厚近薄远原则优选的α值及预测值比较
从表4可见采用厚近薄远原则得出的模型精度更高.取α=0.45,用1996~2007年全部数据建立的二次曲线模型为
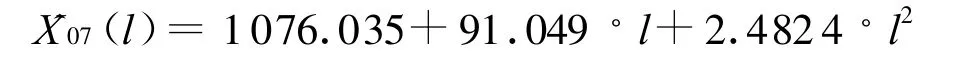
由此可计算出上海市2008~2012年5年用电量的预测值如下:08=1169.5664 GW·h,09=1268.0626GW·h,10=1371.5236GW·h,11=1479.9494GW·h,12=1593.34GW·h.
5 结 论
本文实验证明,采用厚近薄远原则优选α值得出的预测值比采用远近相同原则得出的预测值更为精确,效果更好.在实际电力负荷预测中运用厚近薄远的原则建立指数平滑法模型,会得到更好的效果,带来更大的经济效益.
[1]牛东晓,曹树华,卢建昌.电力负荷预测技术及其应用[M].2版.北京:中国电力出版社,2009.
[2]康重庆,夏 清.电力系统负荷预测[M].北京:中国电力出版社,2007.
[3]汪琥庭.指数平滑预测法研究的若干新结果[J].预测,1994(2):52-55.
[4]康重庆,夏 清,应用于负荷预测中的回归分析的特殊问题[J].电力系统自动化,1998,22(10):38-41.
[5]吉培荣,张玉文,优选平滑系数的指数平滑法电量预测系统[J].电网技术,1996,20(16):52-56.
[6]钱任庚,一种利用0.618优选法优化平滑系数的方法[J].系统工程,1994,12(2):59-61.
