基于HFI代数的模糊命题演算的形式演绎系统

秦学成，刘春辉

（赤峰学院 初等教育学院，内蒙古 赤峰 024000）

基于HFI代数的模糊命题演算的形式演绎系统

秦学成，刘春辉

（赤峰学院 初等教育学院，内蒙古 赤峰 024000）

建立了一个基于HFI代数的模糊命题演算形式系统H*,研究了这个系统的基本特征.并讨论了该系统关于建立在HFI代数上语义的完备性.

HFI代数；模糊逻辑；演绎系统；完备性

1 引言与预备

随着智能计算机的出现,模糊控制技术得到了飞速的发展.而各种模糊控制又是以其特定的模糊推理和模糊逻辑为基础的.在各种逻辑系统中,“蕴涵”是一个基本的逻辑连接词,通常称之为蕴涵算子.为了适应不同的模糊推理的需要,国内外的专家和学者引入了许多不同的蕴涵算子,如Zadeh算子,Kleene算子,覵ukasiewicz算子,G觟del算子和王国俊教授提出的R0算子等.为了研究蕴涵算子的共同本质,吴望名教授引入了Fuzzy蕴涵代数和Heyting型Fuzzy蕴涵代数(简称HFI代数)的概念,并研究了它们的一些基本性质[1].

值得注意的是,利用代数赋值的方法来研究命题逻辑问题,无论是在经典逻辑还是在非经典逻辑中都是极为重要的.然而,从某种意义上讲,代数赋值的方法在逻辑上的等效性主要取决于赋值域的合理选择和赋值本身所具有的良好性质.正是因为如此,人们从不同的逻辑背景出发提出了各种不同的语义代数结构,如MV代数[2],BCK代数,格蕴涵代数[3],BL代数,剩余格和R0代数[4-5]等.对这些逻辑代数的研究和思考,已经得到了国内外学者的广泛关注,获得了许多良好的结果.并分别以它们为基础建立了各种各样的命题演算的形式系统[6-9].本文我们建立了一个基于HFI代数的模糊命题演算的形式系统H*,研究了这个系统的基本特征,并讨论了该系统关于建立在HFI代数上语义的完备性.

为了讨论方便,我们首先给出一些预备知识:

定义 1.1[1]（2，0）型代数（X，→，0）称为 Heyting型Fuzzy蕴涵代数,简称HFI代数,如果对于任意的x,y,z∈X都有

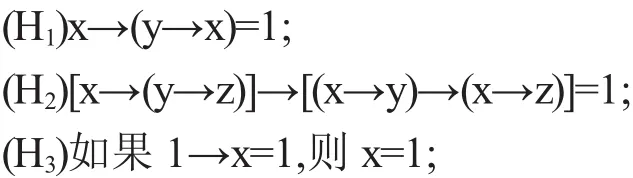
引理 1.2[1]设(X,→,0)是HFI代数,在X上定义二元关系≤使得坌x,y∈X,x≤y当且仅当x→y=1,则(X,≤)是一个偏序集,且分别以0和1为最小元和最大元.

引理 1.3[1]设(X,→,0)是 HFI代数,则坌x,y,z∈X都有

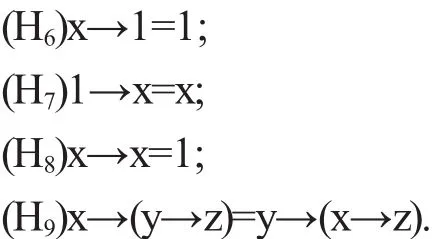
2 模糊命题演算的形式演绎系统H*

定义2.1 模糊命题演算的形式演绎系统H*由以下几部分构成:

(I)公式集F(S):一个含有特定公式0的→型自由代数.即:①∈F(S);②若 A,B∈F(S),则 A→B∈F(S).

(II)公理集Axm(H*).Axm(H*)由以下形式的公式组成:

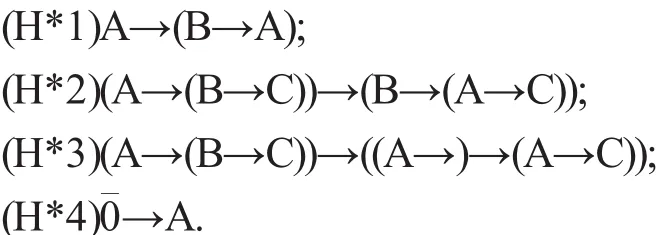
(III)推理规则:MP规则.即由A和A→B推得.

在系统H*中,一些关于逻辑的术语和记号是自明的(见文献[4]和[5]).如定理,从公式集Г的推演以及可证等价等等.我们仍用记号┝A,Г┝A,A≈B分别表示A是H*中的定理,Г结论,A和B可证等价.

注2.2 显然,在系统H*中,推理规则MP是保定理的.即如果┝A且┝A→B,则┝B.

定理2.3 在系统H*中,三段论推理规则HS成立.即{A→B，B→C}┝A→C.

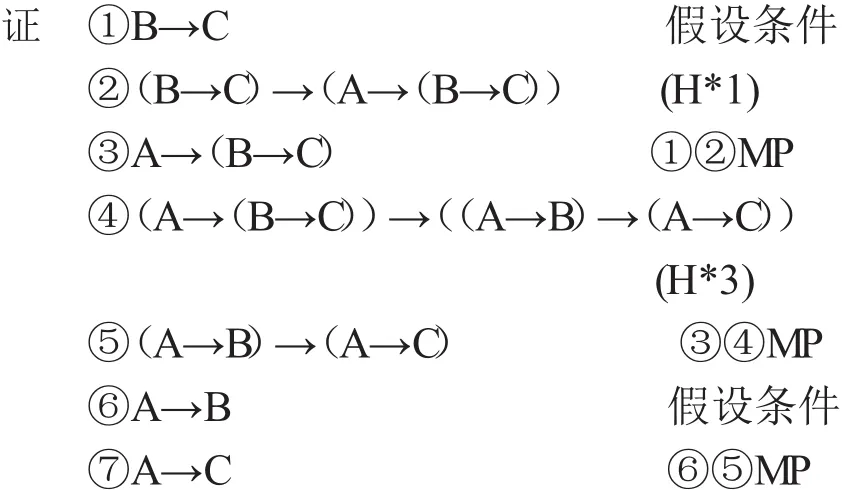
这样就证明了在系统H*中,三段论推理规则HS成立.

推理2.4 在系统H*中,如果┝A→B且┝B→C,则┝A→C.

定理2.5 在系统H*中,以下公式都是定理:(ii)(A→B)→((C→A)→(C→B)是定理的证明如下:

(v)由(iv)可得├A→((A→0)→0),即 A→┐┐A是系统H*中的定理.

定理2.6 在系统H*中,演绎定理成立.即设Г奂F（S）,A，B∈F（S）,如果 Г∪{A}├B,则 Г├A→B.

证 类似于文献[5]中关于经典逻辑的演绎定理的证明,这里从略.

引理 2.7 在系统 H* 中,坌A，B，C∈F（S）有

(1)如果├B,则├A→B;

(2)如果├A→（B→C）,则├B→（A→C）;

(3)如果├A→B,则├（B→C）→（A→C）且├（C→A）→（C→B）.

证 (1)因为由(H*1)知├B→（A→B）,故由├B及系统H*中MP规则保定理便得├A→B.

(2)因为由(H*2)知├（A→（B→C））→（B→（A→C））,故由├A→（B→C）├B及系统 H*中 MP规则保定理便得├→（A→C）.

(3)因为由定理 2.5(iii)可知├（A→B）→（（B→C）→（A→C））,故由├A→B及系统 H*中 MP规则保定理便得├（B→C）→（A→C）.类似地由定理2.5(ii)和MP规则保定理有可得├（C→A）→（C→B）.

定义2.8 设A，B∈F(S),如果├A→B且├B→A,则称A与B可证等价,记为A≈B.

定理2.9 在系统H*中,可证等价关系≈是一个→型同余关系.并且所有定理恰好形成一个等价类,记为[T].

证 由定理2.5(i),≈的定义和推论2.4分别可知≈是自反的,对称的和传递的,从而≈是F（S）上的一个等价关系.为证≈是一个同余关系,下面只需证明坌A，B，C，D∈F（S）,如果 A≈B 且 C≈D,则 A→C≈B→D.事实上,设 A≈B 且 C≈D,则├A→B,├B→A,├C→D且├D→C.故根据引理2.7(3)以及├A→B和├D→C可得├（B→D）→（A→D）且├（A→D）→（A→C）,从而由推论 2.4便得├（B→D）→（A→C）.类似地由引理2.7(3)以及├B→A和├C→D又可得├（A→C）→（B→D）.故由定义2.8便得A→C≈B→D.这样就证明了可证等价关系≈是一个→型同余关系.

现在设├A.若 B∈F（S）,A≈B,则├A→B,故由系统H*中MP规则保定理知├B.即B∈[T].反之如果├B,则由引理2.7(1)可知├A→B且├B→A,故由定义2.8知A≈B.即H*中所以定理恰好形成一个等价类[T].进而定理结论成立.

定理2.10 假设F（S）是系统H*中的公式集,≈是F（S）上的可证等价关系,则商集

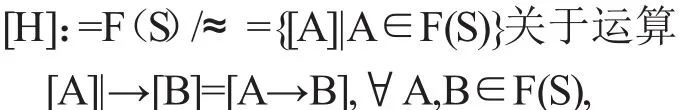
证 由定理2.9可知系统H*中的可证等价关系≈为F(S)上的同余关系,从而保证了等价类间的运算|→与各类中的代表元的选取无关,即|→为F(S)上的二元运算.下证(F(S)/≈,|→,0)是一个 HFI代数.事实上,

(1)由(H*1)知[A]|→（[B]|→[A]）=[A]|→[B→A]=[A→（B→A）]=[T]，故(H1)成立.

(2)由(H*3)可得 （[A]|→（[B]|→[C]））|→（（[A]|→[B]）|→（[A]|→[C]））=[A→（B→C）]|→[（A→B）→（A→C）]=[（A→（B→C））→（（A→B）→（A→C））]=[T],故(H2)成立.

(3)如果[T]|→[A]=[T],则[T→A]=[T],故 T→A≈T,从而由定理2.9可得├T→A,又由引理2.7(1)显然有├A→T,故 A≈T,即[A]=[T].故(H3)成立.

(4)如果[A]|→[B]=[B]|→[A]=[T],则[A→B]=[T],故根据定理2.9可知├A→B且├B→A,于是A≈B,即[A]=[B].故(H4)成立.

(5)由(H*4)可知[0]|→[A]=[0→A]=[T],且[T]=[0→0]=[0]|→[0],故(H5)也成立,从而(F(S)/≈,|→,0)是一个HFI代数.

3 系统H*的语义和完备性

在本节中,我们将为系统H*在一般的HFI代数上建立相应的语义,并推论其完备性.

定义3.1 设(H→,0),是HFI代数,F(S)是系统H*的公式集,A∈F(S).令v:F(S)→H.

(1)如果v是从F(S)到H的同态,即v(0)=0且v(A→B)=v(A)→v(B),则称v是一个→型H-赋值,记全体H-赋值之集为Ω（H）.

(2)如果坌v∈Ω,恒有v(A)=1,则称公式A是一个H-重言式,记作莸HA.

定理3.2(H-可靠性) 设（H，→，0）是任意的HFI代数,F（S）是系统H*的公式集,A∈F(S).如果├A,则莸HA.

证 这只需证明系统H*中的每条公理都是H-重言式,且MP规则保H-重言式即可.事实上,坌v∈Ω（H）,A，B，C∈F（S）,由 HFI的定义 1.1 和引理1.3易得

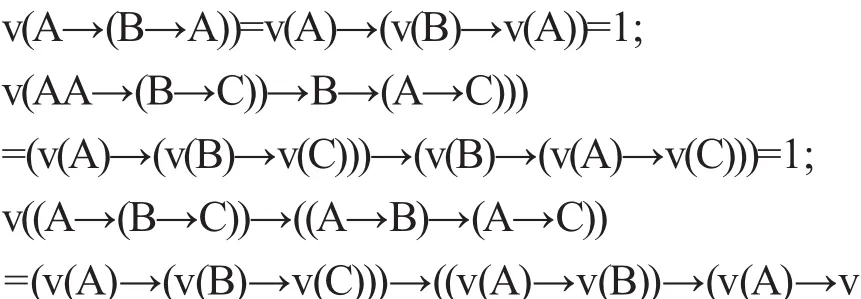
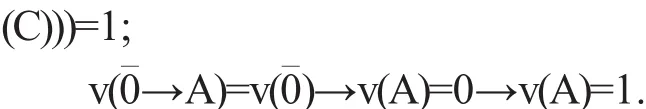
从而系统H*中公理(H*1)—(H*4)都是H-重言式.

又如果A和A→B都是H-重言式,即坌v∈Ω都有v(A)=1且v(A→B)=1,则有v(B)=1→v(B)=v(A)→v(B)=1,故MP规则也保H-重言式.从而证明了H-可靠性定理是成立的.

定理3.3([H]-完备性) 设F(S)是系统H*的公式集,A∈F(S),则├A当且仅当莸[H]A.

证 “必要性”:由定理2.10和定理3.2立即可得.

“充分性”:设莸[H]A,则坌v∈Ω([H])有 v(A)=[T].取v 为从 F(S)到[H]的自然投射,即 v:F(S)→[H]使得 v(X)=[X],坌X∈F(S),则[A]=v(A)=[T],故由定理 2.9便知├A.从而[H]-完备性定理得证.

定理3.4(H-完备性) 设 (H,→,0)是任意的HFI代数,坌A∈F(S),则├A当且仅当莸HA.

证 必要性由H-可靠性定理可得.充分性由[H]=F(S)/≈为HFI代数和定理3.3既得.

以上我们建立了一个基于HFI代数的模糊命题演算的形式演绎系统H*,并为该系统在一般的HFI代数上建立了语义理论,从而讨论了该系统的完备性.这为模糊推理在应用领域又提供了一个良好的基础框架和数学模型.

〔1〕吴望名.Fuzzy蕴涵代数 [J].模糊系统与数学，1990,4(1):56—64.

〔2〕刘练珍,王国俊.Fuzzy蕴涵代数与MV代数[J].模糊系统与数学，1998,12(12):21—25.

〔3〕徐扬.格蕴涵代数[J].西南交通大学学报,1993,28(1):20-27.

〔4〕王国俊.非经典数理逻辑与近似推理[M].北京:科学出版社,2006.

〔5〕王国俊.数理逻辑引论与归结原理(第二版)[M].北京:科学出版社,2006.

〔6〕裴道武,王国俊.形式系统L*的完备性及其应用[J].中国科学(E 辑)，2002,32(1):56-64.

〔7〕朱怡权.格蕴涵代数与Lukasiewicz逻辑系统[J].内蒙古师范大学学报 (自然科学版)，2004,35(2):121-123.

〔8〕傅丽.次BL代数的推理系统[J].陕西师范大学学报，2002,30(1):17—21.

〔9〕裴道武.强正则剩余格值逻辑系统LN及其完备性[J].数学学报，2002,45(4):745—752.

O141.1；O153.1

A

1673-260X（2010）01-0004-03