火药起动系统双喉道管路特性分析

2010-10-15孙海雨刘志让

火箭推进 2010年1期

孙海雨，刘志让，明磊

（1西安航天动力研究所，陕西西安710100；2航天推进技术研究院，陕西西安710100；3中国空军工程大学，吉林长春130022）

0 引言

泵压式液体火箭发动机有多种起动方式，火药起动方式由于具有起动能量高、体积小、系统结构简单、工作可靠及起动加速能力好等特点，被广泛应用于泵压式液体火箭发动机中。

在整个液体火箭发动机工作过程中，起动过程是一个非常重要的阶段。在此期间，所有工作过程参数（流量、压强、涡轮泵转速及温度等）都必须在短暂的时间内从初始状态过渡到主级工作状态，工作过程极为复杂，是发动机能否正常进入主级工况的关键。在发动机的起动过程中，起动系统中的双喉道管路起到了重大作用，因此需要对其进行详细的计算和分析。

1 组成及功能

液体火箭发动机采用火药起动方式时，利用火药起动器中火药燃烧产生的燃气驱动涡轮，从而实现发动机的快速起动。

液体火箭发动机火药起动系统双喉道燃气管路如图1所示，它由火药起动器喷管、涡轮喷嘴以及二者之间的圆柱段管道组成。在发动机的起动过程中，火药起动器必须保持一定的流量、压力和温度，同时避免发动机工况对起动器工作的干扰，为此，在火药起动器燃烧室后安装了火药起动器喷管，设置了喉道；同时，冲压式涡轮要求其入口气流速度为超声速，因而在涡轮入口前安装了涡轮喷嘴，设置了第二个喉道。火药起动器由于自身的工作需要，其燃烧压力比涡轮喷嘴前所需气流总压高很多，因此在燃气传输过程中需要降低燃气的总压，此降压过程也可通过双喉道管路来实现。

2 双喉道管路对火药起动器工作性能的影响

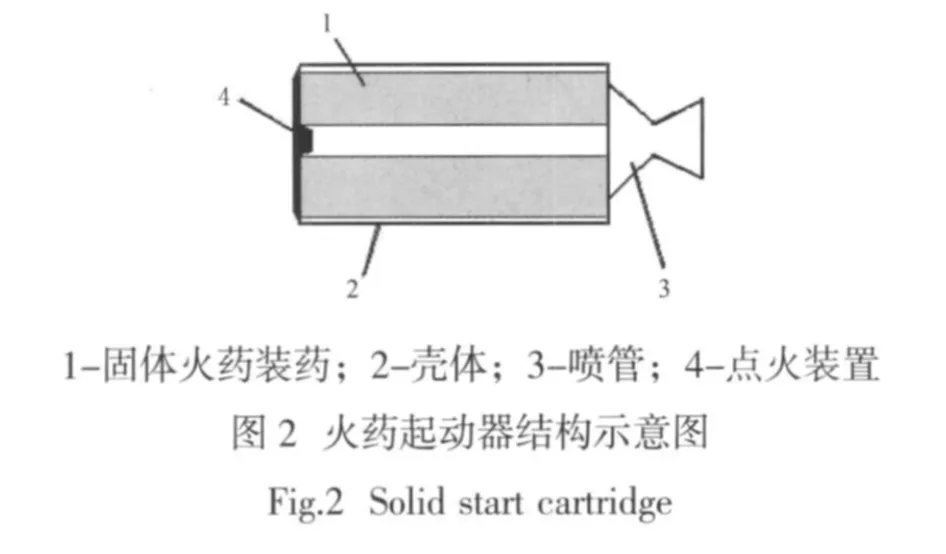
火药起动器由壳体、固体火药装药（简称药柱）喷管以及点火装置组成，主要是通过壳体内火药的燃烧为发动机的起动提供初始能量，如图2所示。对于特定的火药配方，其燃气总温恒定，所以火药起动器的做功特性将取决于燃气总压值的大小。

2.1 火药起动器零维内弹道计算模型

火药起动器内燃气压强的变化由燃气质量生成率、喷管中排出的燃气质量流率以及燃烧室中燃气质量变化率所决定。火药起动器中火药装药常采用单孔圆柱形，且其燃烧方式为端面和侧面燃烧，燃气压强沿其轴向变化不大。此时可有如下假设：

(1)零维假设，即燃气流动参数取其沿轴向的平均值；

(2)火药装药燃烧完全，燃烧产物组分不变，且燃烧温度等于推进剂的等压燃烧温度；

(3)燃气为完全气体，服从完全气体状态方程；

(4)装药燃烧服从几何燃烧定律；

(5)不考虑火药燃烧时的侵蚀效应。

在以上假设下，推导可得起动器零维内弹道计算的微分方程[1]：

式中，Vg为燃气占有的容积，即燃烧室自由容积为火药燃气气体常数；T0为火药燃烧温度；k为燃气绝热指数；为燃烧室平均压强；Ab为装药燃烧面积；At为起动器喷管喉部面积；a、n为燃速公式中的系数，可由试验得出；ρp为推进剂装药密度；φ为流量修正系数；χ为热损失修正参数。

2.2 零维内弹道计算模型验证

利用已有试验数据对零维内弹道计算模型进行验证，图3为某型发动机火药起动器内平均压力试验曲线与计算曲线的对比图。由图3可以看出计算曲线与试验曲线的吻合度很高，说明火药起动器零维内弹道计算模型精度高，可以达到火药起动器工程实际要求。

2.3 双喉道管路的影响

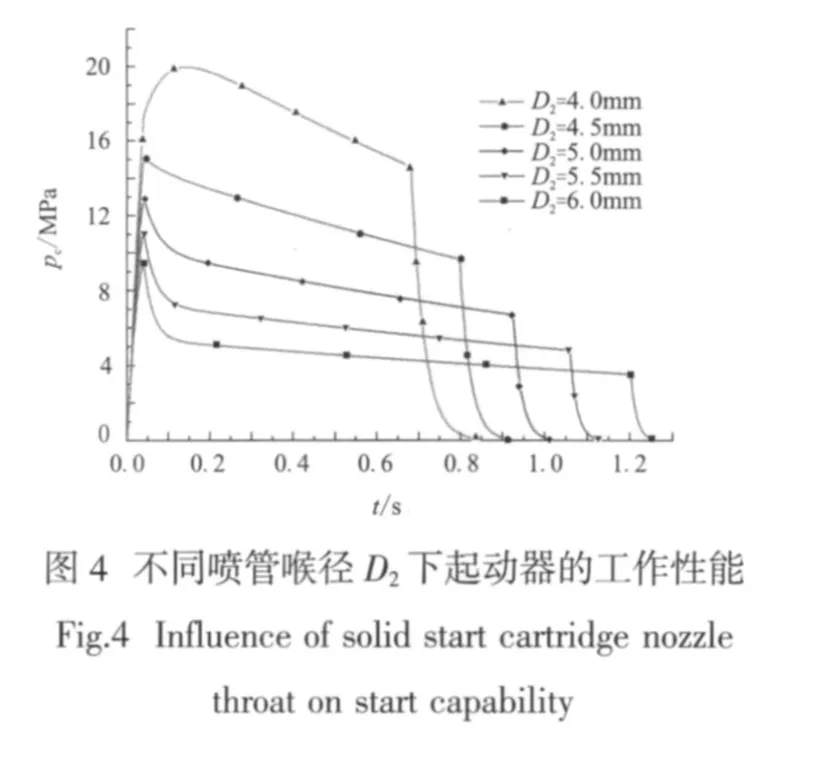
由公式（1）可以看出，火药起动器内燃气总压是火药种类（ρp、R、T0、k）、药拄结构（Ab）以及起动器壳体结构（Vg、At）三类参数的函数。在火药种类、药拄结构以及起动器内径确定以后，火药起动器喷管喉径将决定火药起动器的做功特性。图4为某型号液体火箭发动机火药起动器在不同喷管喉径D2下，燃气总压随时间的变化曲线图。由图4可以看出，火药起动器喷管喉径从4mm增大到6mm过程中，随着D2的增大，火药起动器内燃气总压降低，起动器工作时间增大，而且变化范围较大。由此，根据火药起动器内燃气总压和流量要求，确定火药起动器喷管喉径D2。

3 双喉道管路计算

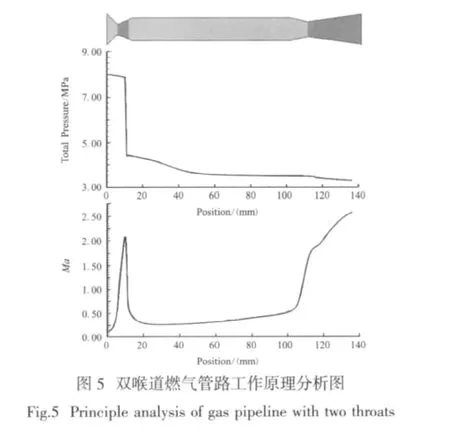
火药起动器中的火药装药点火燃烧，产生高温高压的火药燃气经过双喉道管路传输到涡轮转子前。传输过程中，燃气首先经过火药起动器喷管，在其扩张段中形成一道激波，总压降低；然后经圆柱段管道进入涡轮喷嘴，燃气加速，以超声速喷出，驱动涡轮，使涡轮泵系统工作。图5为燃气管路总压和马赫数的轴向变化图，图中可以清楚地看到燃气降压及加速的过程。

燃气在双喉道燃气管路中流动时，将有多种流态，上述的额定工况流态只是其中的一种组合情况，但是随着入口和出口边界条件的不同，各个部件中的燃气将会有多种流态。火药起动器喷管中存在三种流态，分别是：1-收缩段亚声速，扩张段超声速；2-收缩段亚声速，扩张段一段超声速后形成激波；3-收缩段亚声速，扩张段亚声速。中间圆柱段有三种流态：1-超声速；2-一段超声速后产生激波变成亚声速；3-亚声速。涡轮喷嘴中存在六种流态：1-收缩段亚声速，扩张段超声速；2-收缩段亚声速，扩张段一段超声速后形成激波；3-收缩段亚声速，扩张段亚声速；4-收缩段超声速，扩张段亚声速；5-收缩段超声速，扩张段超声速；6-收缩段超声速，扩张段超声速后形成激波。

火药起动系统为能正常驱动涡轮，使发动机起动符合要求，除双喉道管路流场流态必须为额定工况流态2-3-1以外，管路流场出口总压p02、出口马赫数Ma2以及出口静温T2也要满足相应的范围。双喉道燃气管路的许多变化因素都会对管路流场流态及出口参数产生影响，从而影响发动机的起动性能。为此，建立双喉道燃气管路的计算模型，以分析变化因素对管路流场的影响。

3.1 燃气管路流场计算模型

当对燃气管路流场进行计算时，采用以下假设：

(1)燃气在多喉道喷管中的流动中比热比、气体常数不变；

(2)气流参数沿同一横截面不变，仅沿轴线方向变化，即一维假设；

(3)燃气在双喉道燃气管路中的流动为不可逆绝热流动，即总温保持不变；

(4)燃气在拉瓦尔喷管中产生激波前的流动为等熵流动，考虑喷管中的摩擦损失时，对喷管取一个总压恢复系数，在中间圆柱段中考虑摩擦损失。

在以上假设条件下，有如下计算方程。

质量流量计算方程：

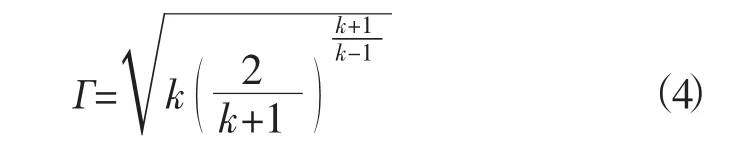
式中，A为燃气管路任意截面处面积；Ma为燃气马赫数；T0为燃气总温；R为燃气气体常数；Г为气动函数，是比热比k的函数[3]。

拉瓦尔喷管计算方程：

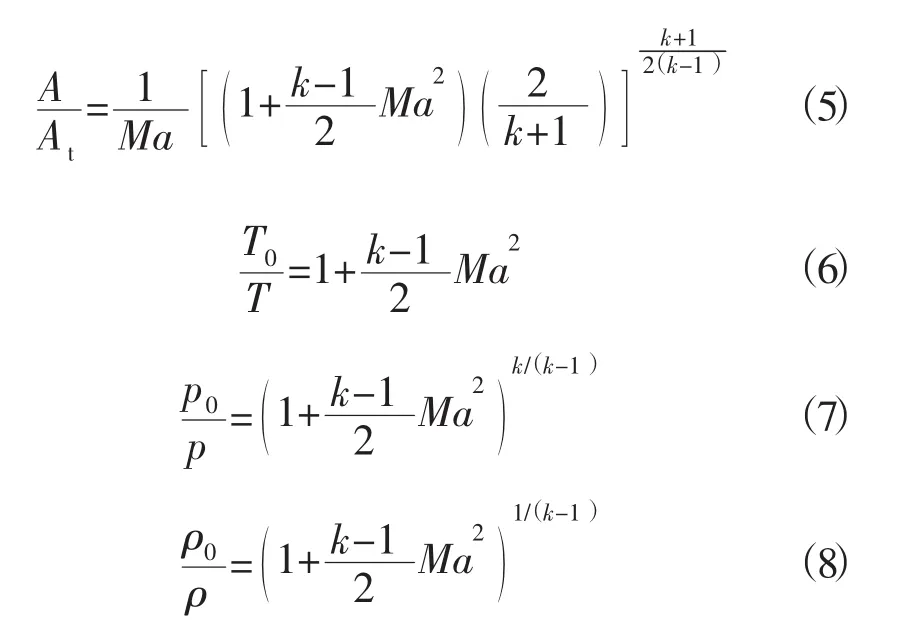
式中，At为喷管喉部直径；T为燃气温度；p为燃气压强；ρ为燃气密度；T0为燃气滞止温度；p0为燃气滞止压强；ρ0为燃气滞止密度[3]。

正激波计算方程：

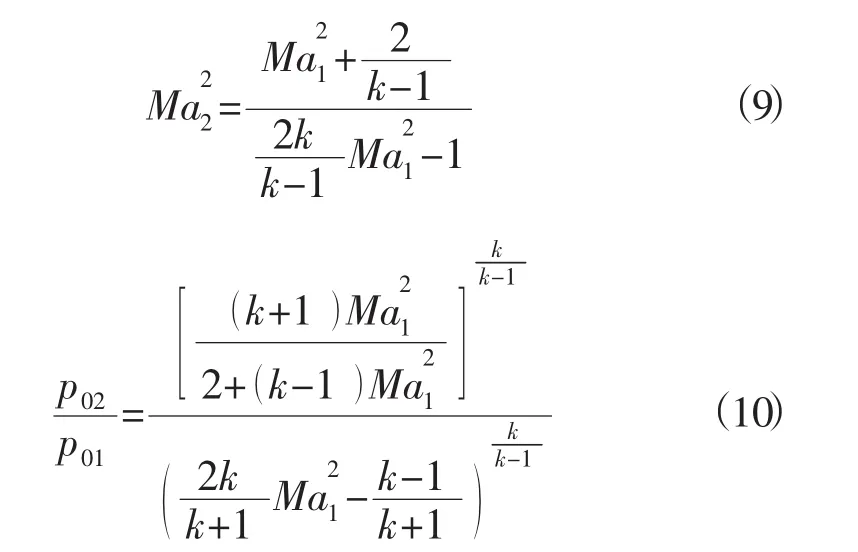
式中，Ma1为激波前马赫数；Ma2为激波后马赫数；p01为激波前滞止压强；p02为激波后滞止压强[3]。

摩擦管计算方程：

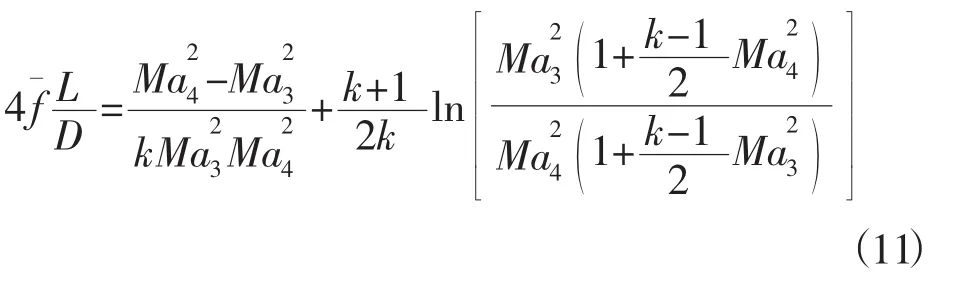
3.2 燃气管路流场计算模型验证

为确定验证所建立燃气管路流场计算模型的可用性，利用该模型对某型号液体火箭发动机燃气管路进行了计算，并将计算结果中双喉道管路圆柱段中间点处的燃气总压p03值与试验数据进行了对比，如图6所示。由图可以看出，模型计算结果与试验结果吻合度较好，说明该模型满足工程精度要求，可以应用。

3.3 燃气管路流场计算结果分析

许多因素将决定双喉道燃气管路的流场特性，包括管路入口总压、火药起动器喷管喉部直径D2、涡轮喷嘴喉部直径D4和涡轮喷嘴出口直径D5等等。起动器喷管喉径D2在火药起动器设计时已基本确定，同时火药起动器内燃气总压即管路入口总压也已确定，所以本节主要分析起动器喷管扩张比、涡轮喷嘴与起动器喷管的喉径比以及涡轮喷嘴扩张比对双喉道燃气管路流场的影响。在计算过程中，管路入口总压取8MPa，管路出口背压为0.35MPa，双喉道管路标准几何结构如图7所示。

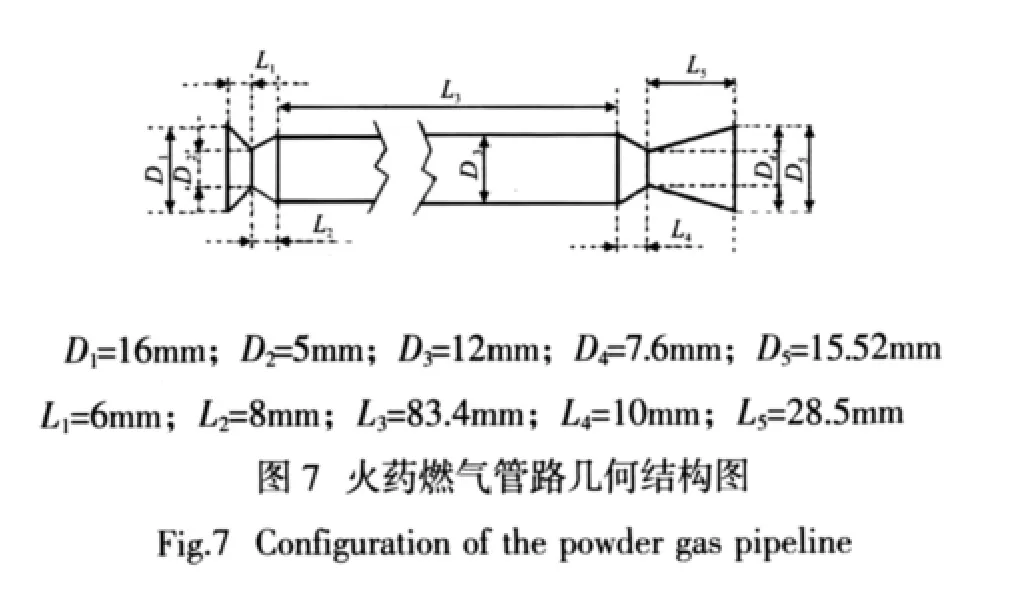
3.3.1 火药起动器扩张比D3/D2的影响

保持入口和出口边界条件以及其他几何结构不变，只改变中间圆柱段直径D3的大小，以分析不同起动器扩张比D3/D2对双喉道燃气管路流场的影响。图8为不同起动器喷管扩张比D3/D2下双喉道燃气管路的马赫数云图，通过计算可知：当扩张比D3/D2＜1.7时，起动器喷管喉部前为亚声速流场，起动器喷管喉部后为超声速流场，即此时双喉道燃气管路流场流态为1-1-5；当D3/D2≥1.7时，起动器喷管扩张段流场中存在激波，涡轮喷嘴流场收缩段为亚声速，扩张段为超声速，即此时燃气管路流场为额定工况流态2-3-1。

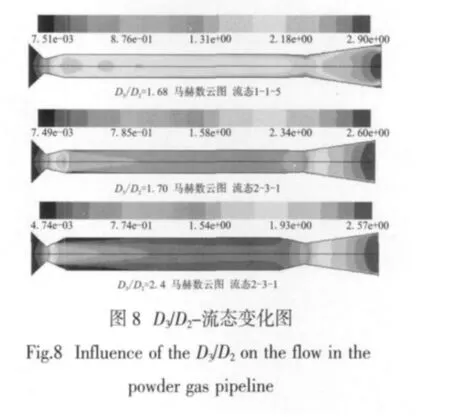
同时计算结果表明，在额定工况流态2-3-1情况下，D3/D2（即D3）的变化对涡轮喷嘴出口处燃气总压、马赫数以及静温影响不大。

3.3.2 涡轮喷嘴与起动器喷管喉径比D4/D2的影响

其他结构不变，起动器喷管扩张比D3/D2为2.4，改变涡轮喷嘴喉径D4值，不同涡轮喷嘴与起动器喷管喉径比D4/D2下双喉道燃气管路的马赫数云图如图9所示。由图可以看出在喉径比从0.4增大到2.4过程中，管路流场共经历了三类流态：

(1)当喉径比D4/D2≤1.2时，双喉道燃气管路涡轮喷嘴喉部以前流场都为亚声速流场，涡轮喷嘴扩张段中为超声速流，即此时流态为3-3-1；

(2)喉径比1.2＜D4/D2≤2.0时，双喉道燃气管路火药起动器喷管喉部达到了声速，并在火药起动器喷管扩张段中形成一道激波，并随着D4/D2的增大而逐渐远离喉部，涡轮喷嘴扩张段中继续保持超声速流场，即此时流态为额定工况流态2-3-1。当D4/D2增大到2.0时，火药起动器喷管扩张段中的激波将位于火药起动器喷管出口截面处；

(3)喉径比2.0＜D4/D2≤2.4时，涡轮喷嘴喉道不足以使燃气在此处到达临界状态，火药起动器喷管喉部以后的双喉道燃气管路流场将都为超声速流，即此时流态为1-1-5。

可见，双喉道燃气管路额定工况流态要求喉径比满足1.2＜D4/D2≤2.0，关注这种流态下喉径比对管路流场出口参数的影响。

图10和图11为其他条件不变时，燃气管路流场出口总压p05、出口马赫数Ma5以及出口静温T5随喉径比变化的计算曲线图。由图10和图11可以看出，在喉径比从1.2增大到2.0过程中，出口总压和出口马赫数增大，出口静温降低。根据燃气管路出口参数的要求，参考此组曲线，即可对双喉道燃气管路的喉径比进行选取。

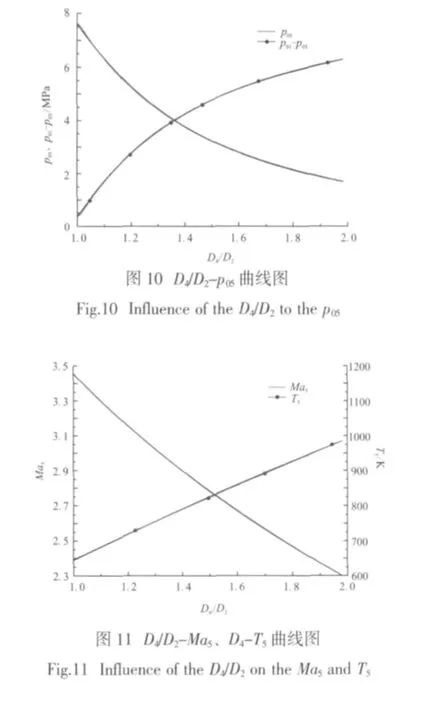
4 设计实例

4.1 设计要求

根据上述双喉道燃气管路的工作特性，对燃气管路结构进行设计。要求该双喉道管路结构满足以下要求：

(1)在某特定药拄结构下,火药起动器内燃气总压平均值为8MPa；

(2)双喉道燃气管路出口总压平均值为3MPa；

(3)双喉道燃气管路出口马赫数不小于2.5；

(4)双喉道燃气管路出口静温为800～900K。

4.2 参数设计

4.2.1 起动器喷管喉径选取

考虑对起动器内燃气总压的影响选取起动器喷管喉径。在选定的火药种类和药拄结构下，对不同起动器喉径下的起动器内燃气总压随时间变化情况进行计算，计算结果如图4所示。设计要求起动器内燃气总压平均值为8MPa，故根据计算曲线选择起动器喷管喉径D2=5mm。此时，起动器燃气总压在主要工况段从9MPa变化到7MPa，起动器工作时间0.925s，满足性能要求。

4.2.2 起动器喷管扩张比选取

在入口总压为8MPa，D2=5mm条件下，为确保双喉道燃气管路为额定工况流态，取起动器喷管扩张比D3/D2为2.4，即D3=12mm。

4.2.3 喉径比选取

入口总压为8MPa条件下喉径比对双喉道管路流场的影响如图7～图9所示，双喉道燃气管路流场为额定流态2-3-1，要求喉径比满足1.2＜D4/D2≤2.0。同时，在额定流态时，燃气管路出口总压由喉径比决定。根据出口总压p02=3MPa要求，由图8中曲线可以确定喉径比D4/D2=1.52。

至此，由所选取的起动器喷管喉径、涡轮喷嘴与起动器喷管的喉径比以及涡轮喷嘴扩张比，即可确定双喉道燃气管路起动器喷管喉径D2=5mm，中间圆柱段直径D3=12mm，涡轮喷嘴喉径D4=7.6mm。