大密度比两流体系统计算的一种改进模式

汪迎春,唐洪武,汪德,唐 亮

(1.蚌埠学院食品与生物工程系,安徽蚌埠 233030;2.河海大学水利水电学院,江苏南京 210098;3.中国水电建设集团国际工程有限公司,北京 100048)

对于密度相近的两流体,Δt时间内网格单元密度可以近似认为不变,但如果两流体密度差异很大或者时间步长Δt较大,网格单元密度在Δt时间内相对变化需要考虑,这时密度的变化将对计算结果产生影响.大密度比两流体问题的求解需增加密度方程

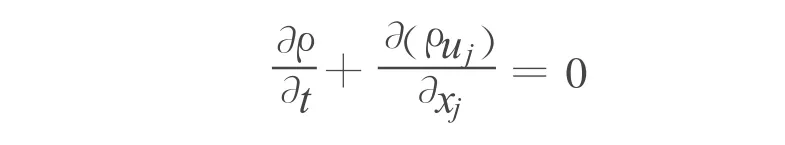
式中:ρ——流体密度;uj——流速标量;t——时间;xj——空间坐标.

目前常见的解决此类问题的方法有2种:一种是令时间步长Δt网格单元密度不变的方法,这种方法适用于弱密度比的两流体问题;另一种是通过增加密度方程并进行耦合求解的方法,这种方法适用于大密度比的两流体问题.直接求解密度方程,会使计算过程中的非线性问题更加突出,还会产生密度越界现象.本文通过对动量方程的一些变换,把密度方程和动量方程统一为一个积分形式,从而有效地解决了大密度比问题.

1 控制方程

对于满足连续条件不可压缩的两相流,其连续方程、密度方程和动量方程为

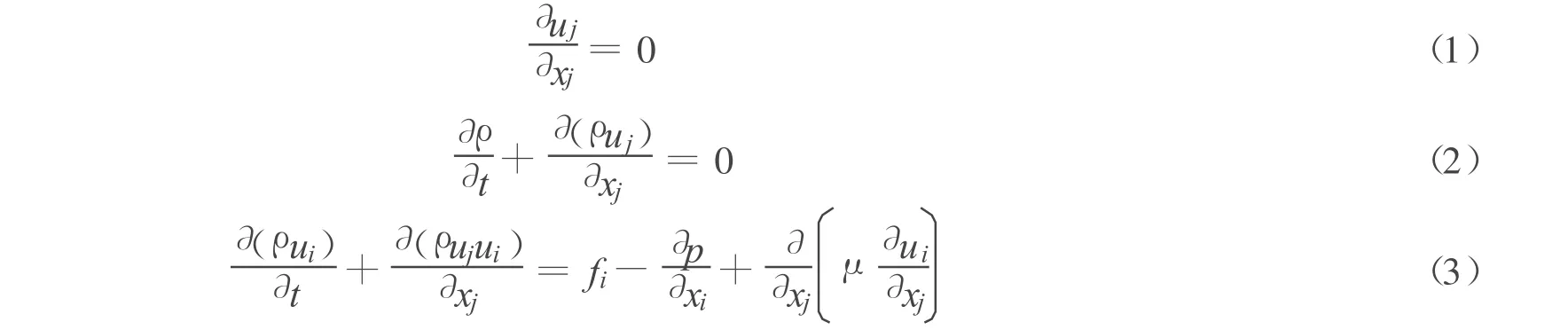
式中:fi——质量力;p——压强;μ——动力黏度.

式(3)左边第1项可变换为

代入式(3)得

方程(4)的离散采用非结构同位网格,物理变量布置在单元中心,如图1所示,用有限体积法离散.将式(4)写成微分方程的积分形式

式中:φ——物理变量;φp——控制体中心的物理变量;Sφ——源项;n——单元边界A的外法向单位向量;d A——面积分微元;d V——体积分微元;u——流速向量.

从方程(5)可直观地看出,对流项的稳定性得到了改善.经以上变换,方程(2)和(3)组合成了方程(5),只需求解方程(1)和(5)即可.

对于方程(5),对流项离散可用二阶迎风格式,单元边界均值 φe由迎风单元直接线性插值得到,

式中:φu——迎风单元中心物理量;(gradφ)u——迎风单元物理量梯度;d r——从迎风单元中心至单元面的距离矢量.

其中的单元中心梯度由高斯公式计算:

图1 网格单元Fig.1 Distribution of cell variables

式中:Aji——单元j面的i方向面积分量;φj——界面处物理变量均值,可直接通过线性插值求得,如果是高度扭曲的畸变网格,则会引入网格误差;α——保证重构不导致局部极值产生的限制性因子,0≤α≤1.扩散项的离散方法可参考文献[1].

2 速度压力耦合与相界面的处理

不可压缩流体N-S速度压力耦合方程的求解方法有很多,由于人工压缩法[2-6]形式简单,且可以获得很高的精度,本文采用人工压缩法.其中,伪时间导数项的离散采用一阶向后差分格式,物理时间项的离散采用二阶向后差分格式,对流项的离散采用二阶迎风格式,扩散项的离散采用中心差分格式.两相流界面的追踪采用Level Set方法[6-10].

3 算 例

本文对Rayleigh-Taylor不稳定分层问题[11]进行了数值模拟.

Rayleigh-Taylor不稳定分层系指上下两层不可压缩的黏性流体,如图2所示.上层为重质流体,其密度和运动黏度分别为 ρ1,ν1;下层为轻质流体,其密度和运动黏度分别为 ρ2,ν2.ρ1/ρ2=998/499=2,ν1/ν2=1.初始界面扰动为

图2 Rayleigh-Taylor不稳定分层问题定义Fig.2 Definition of Rayleigh-Taylor unstable layer problem

式中:u,v——x,y方向的流量;Uref——参考点流速.

本研究取α=0.25,Re=283,左右两边取对称边界,上下两边取固壁边界.

量纲一的初始压力取为

其中

式中:pref——参考点压力;g——重力加速度;p(y)——基准压力.因

此,上层流体

下层流体

其中

图3为采用大密度比常用处理方法和本文处理方法计算得到的分层界面形状.由图3可以看出,2种大密度比处理方法计算得到的分层界面形状很接近,由于离散格式未采用高精度的格式,故不稳定界面向下翻转的卷舌处模拟还不够精细.图3(a)由于采用常用的处理方法,界面坦化严重,结果和理论分析成果[12]出现较大的差别.

图3 计算的分层界面形状Fig.3 Shapes of calculated layer interfaces

4 结 语

本文把密度方程和动量方程组合成一个方程,变换为一个积分形式,提出了一种新的处理大密度比两流体系统的方法.该方法有效地避免了两方程的耦合问题以及单独求解密度方程带来的一些不合理现象.数值试验表明,本文方法是有效的,可用于大密度比的两流体问题的数值模拟和分析.

[2]薛具奎,赵金保.人工压缩法数值模拟非定常不可压缩热对流流场[J].西北师范大学学报:自然科学版,1998,34(2):32-37.(XUE Ju-kui,ZHAO Jin-bao.Numerical simulation for unsteady incompressible thermoconvective flow with artificial compressibility method[J].Journal of Northwest Normal University:Natural Science Edition,1998,34(2):32-37.(in Chinese))

[3]陈传淡.守恒双曲型方程式激波计算区域分解法中的追踪及人工压缩方法[J].厦门大学学报:自然科学版,1999,38(3):329-333.(CHEN Chuan-dan.Tracing and artificial compression method of theshock′s calculation for the conservative hyperbolic equation in domain decomposition[J].Journal of Xiamen University:Natural Science,1999,38(3):329-333.(in Chinese))

[4]朱自强,贾剑波.三角翼大迎角不可压粘流的数值模拟[J].力学学报,1996,28(6):736-740.(ZHU Zi-qiang,JIA Jian-bo.Numerical Simulation of incompressible viscous flow over a deltawing at high angle of attack[J].Acta Mechanica Sinica,1996,28(6):736-740.(in Chinese))

[6]汪迎春.运动界面模拟技术及在环境分层流中的应用[D].南京:河海大学,2007.

[7]OSHERS,SETHAIN J A.Fronts progagating with curvature-dependent speed:algorithms based on Hamilton-Jacobi formulations[J].J Comput Phys,1988,79(1):12-49.

[8]刘儒勋,王志峰.数值模拟方法和运动界面追踪[M].合肥:中国科技大学出版社,2001.

[9]TSAI Y H R.Rapid and accurate computation of the distance function using grids[J].JComput Phys,2002,178(1):175-195.

[11]FELECY F J,PLETCHER RH.Numerical simulation of free surface flows in closed containers using free surface capture approach,in advances in computational methods in fluid dynamics[J].Am Soc Mech Eng,1994,196:33-51.

[12]ZHAO Yong,TAN Hsiang-hui,ZHANG Bai-li.A high-resolution characteristics-based implicit dual time-stepping VOF method for free surface flow simulation on unstructured grids[J].Journal of Computational Physics,2002,183(1):233-273.