基于小波变换的钢箱梁应力监测多尺度分析
2010-10-11刘文淑林咸志陈志坚
刘文淑,林咸志,薛 涛,陈志坚,陈 青
(1.南京大学地球科学系,江苏南京 210093;2.浙江华光潭水力发电公司,浙江临安 311322;3.河海大学地球科学与工程学院,江苏南京 210098)
苏通大桥是目前世界上第一大跨径斜拉桥[1],主跨1 088m.为了降低施工风险,苏通大桥主桥钢箱梁吊装采用先边跨后主跨的方案,同时辅助安全监测手段.安全监测只针对主跨23个标准梁控制截面的顶板、底板及结构敏感变化部位(如U肋、焊缝)进行.测点布置如图1所示.
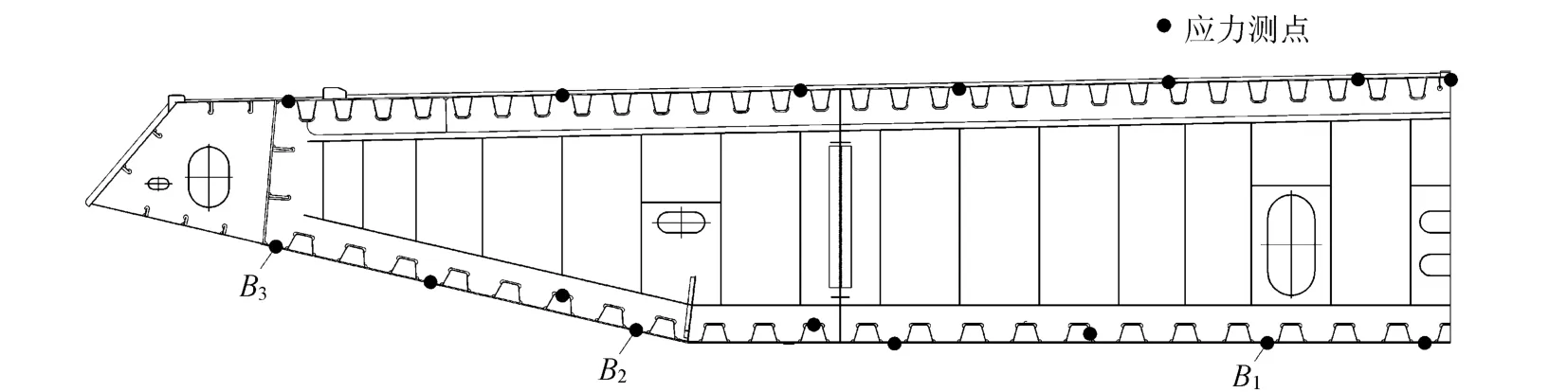
图1 半幅钢箱梁标准横断面应力测点布置Fig.1 Layout of stress measuring points in standard cross section of half of steel box girder
实测数据表明,钢箱梁架设过程中,主梁应力处于复杂的波动状态:既有钢箱梁吊装、斜拉索张拉等施工荷载产生的应力骤变,也交织有传感器精度、电磁干扰、传感器埋设状态等传感器自身因素及日照辐射、昼夜温差、风等气象因素的重要影响.这些噪声幅值大,分布广,用传统的时域或频域滤波往往不能取得预期效果[2-3].为此,本文针对小波多尺度分析理论在数据处理中的优势[4-7],结合实测气象资料,对实时测量数据进行了小波多尺度去噪处理[8-10].
1 小波多尺度去噪模型
苏通大桥钢箱梁施工安全监测是长期的实时在线监测,传感器数量较多,数据量非常大,加之监测信号包含了各种激励(如施工荷载、环境因素等)引起的结构响应,因而具有多尺度特征.其应力观测数据的模型形式可表示为

式中:s——实测数据;f——有效数据,通常为低频信号或一些比较平稳的信号;e——1级高斯白噪声,通常表现为高频信号;ε——噪声级.
小波多尺度去噪就是将实测数据s中的有效数据f分解到粗尺度上,以反映结构响应的趋势性,而高频信号e则被分解到细尺度上,将其置零后再进行重构,即得到去噪后的平滑信号和细节信号.然而,原始数据中的高频信息并不都是噪声所致,如果简单地将所有分解出来的高频信息一概去掉,将会导致信号失真.因此,去噪时需要根据信号和噪声的小波变换系数在不同尺度下的特性选择参数λ(称之为阈值),并通过软阈值化[11]处理后,分层剔除噪声影响.
由于小波在不同尺度下随着尺度的增大,其小波变换系数将逐渐减小,所以在不同尺度下选取相同的阈值显然不足.自适应阈值法[12]认为每一级尺度都相互独立,并寻找与之最匹配的阈值来进行消噪.该方法可以更有效地去除噪声和保留有效信息.
2 实例与分析
苏通大桥钢箱梁应力监测始于2007年3月28日.由于气象因素对钢箱梁应力观测结果的影响较大,故代表性地选择测点B3自2007年6月13日13:20至15日6:20期间(环境温度变化幅值只有1.3℃,而最大横桥向风速为8.5m/s)共40h的实测应力与横桥向风速进行比对(图2),测点B 1,B2和B3自2007年6月16日0:00至23日0:00期间共168h的实测应力与温度进行比对(图3).图中 σB1,σB2,σB3分别为测点B1,B2,B3的应力值,θ为温度值,测量频度均为1h.此时工况为:大桥已经合拢,且呈全飘浮状.
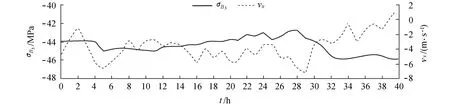
图2 测点 B3实测应力σB3与风速 vx对比关系Fig.2 Relationship between measured stress and wind speed at measuring point No.3
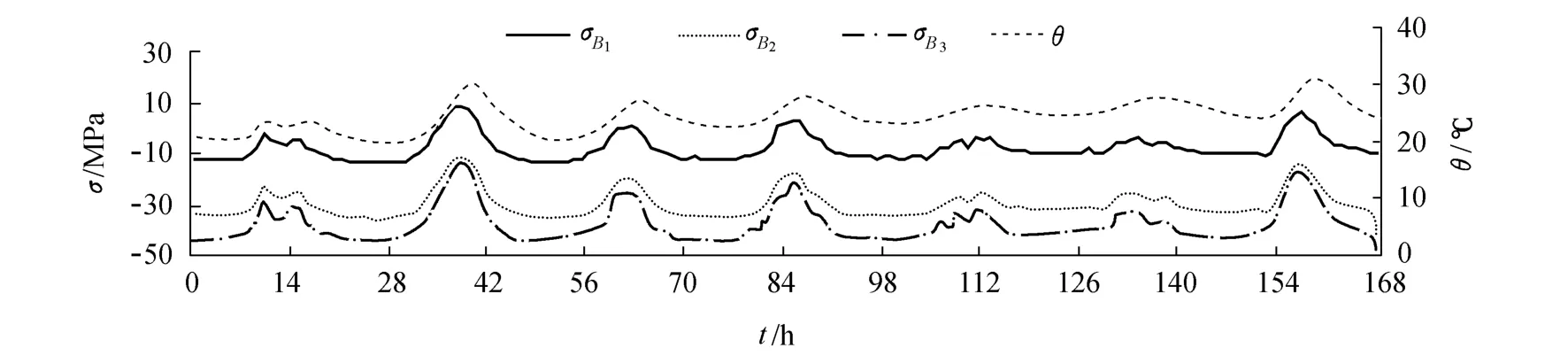
图3 实测应力与温度时程曲线对比关系Fig.3 Relationship between measured stress and temperature
图2显示:风速较小时,风荷载对主梁应力的影响较小;而风速较大时,它的随机性和方向性使得应力时程曲线产生无规律的波动,因此,在进行静力分析时可以将其与其他偶然因素合并考虑.这些偶然荷载产生的噪声干扰往往表现为一些高频信号,故采用db4小波基函数对其进行小尺度分解,即可消除偶然荷载及风荷载产生的干扰,如图4所示.图中σ′B1,σ′B2,σ′B3分别为测点B1,B2,B3剔除随机噪声后的应力值,Δθ为昼夜温差.从图4可知,曲线光滑性很好,且与原曲线有着很好的相似性.因此,可以认为高频部分的随机噪声已被剔除,而温度变化产生的应力响应则以低频信号的形式叠加在观测结果中.从图3可以看出,温度与应力曲线的变化趋势几乎一致,只是底板温度变化趋势滞后于应力响应趋势,这是因为钢箱梁底板吸热过程滞后于结构变化过程所致.

图4 剔除随机噪声后的应力与昼夜温差对比关系Fig.4 Relationship between stress after denoising and difference in temperature
表1给出了25号梁段顶板、底板分析时段内的温度特征值.从表1可以看出:钢箱梁顶板温度变化非常显著,最大温差达28.7℃;而对应底板温度变化较小,最大温差仅11.3℃.另外,白天太阳辐射引起的顶板温度比底板温度平均高9.7℃,形成正温差,而夜间则是底板温度高于顶板温度,平均温差为1.6℃,为负温差.因此,图4很显然表现了温度应力随昼夜温差变化的显著趋势.
由此可知,钢结构的导热性虽然好,但对于高大截面来说,较大的温度梯度会产生显著的温度应力,其应力幅大小因测点位置不同而不同.在此,测点B1,B2,B3的应力幅分别为-5.2~17.0MPa,-5.7~19.0MPa,-6.3~25.1MPa.为了消除温度应力的影响,仍然采用db4小波基函数,并将尺度增大到5层进行阈值降噪处理,消噪后的应力时程曲线如图5所示.图中 σ″B1,σ″B2,σ″B3分别为测点 B1,B 2,B3消噪后的应力值.
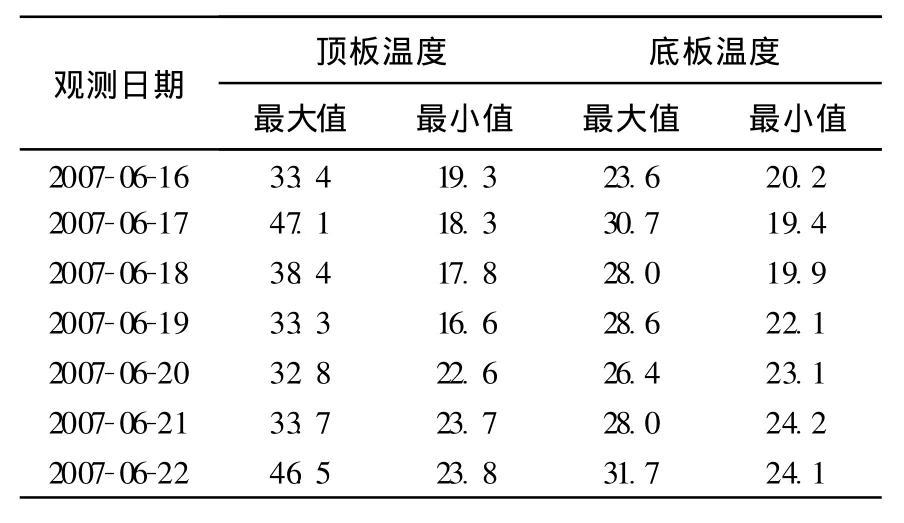
表1 25号梁段顶板、底板温度特征值Table1 Temperature eigenvalues of top and bottom planes of beam No.25 ℃
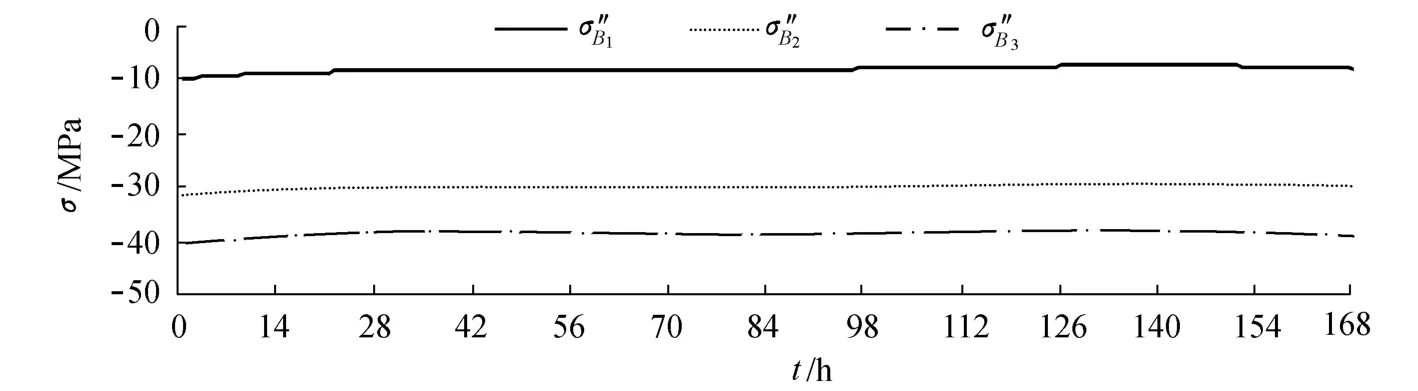
图5 消噪后的应力时程曲线Fig.5 Time history curves of stress after denoising
3 结 论
a.钢箱梁架设过程中,主梁应力处于复杂的波动状态,分层剥离不同因素的干扰,多尺度小波分析方法较为简单易行.风等随机因素表现为高频信号,可用较小尺度进行分解;而对于昼夜温差产生的低频信号,则首先通过较大的尺度进行分解,然后对信号进行重构,即可达到消噪的目的.
b.小波多尺度阈值去噪应用最广泛的是Donoho的软阈值法.该法在每一级尺度上都采用了同一阈值,不能在每级尺度上将信号与噪声进行最大分离,在此基础上引进自适应阈值,将每一级尺度都视为相互独立,分别选用与之最匹配的阈值进行除噪,可以最大程度地去除每一尺度上的噪声.
c.大跨度桥梁建设过程中的影响因素复杂,施工难度大,要想对各个因素进行深入分析,还需有针对性地进行监测.
[1]游庆仲,董学武,吴寿昌.苏通大桥基础工程的挑战与创新[J].中国工程科学,2007,9(6):22-26.(YOU Qing-zhong,DONG Xue-wu,WU Shou-chang.Challenge and innovation in Sutong bridge foundation project[J].Engineering Science,2007,9(6):22-26.(in Chinese))
[2]杨惠珍,张宇波.数字滤波方式在监控系统中的应用[J].洛阳学院学报,1999,20(3):53-55.(YANG Hui-zhen,ZHANGYu-bo.Thedigital filter measures in the microcomputer systems[J].Journal of Luoyang Institute of Technology,1999,20(3):53-55.(in Chinese))
[3]栾瑞明.Kalman滤波理论在滑坡监测中的应用[J].地壳形变与地震,1994,14(1):52-59.(LUAN Rui-ming.Application of Kalman filtering theory to the landslidemonitoring[J].Crustal Deformation and Earthquake,1994,14(1):52-59.(in Chinese))
[4]MALLATSG.A theory for multiresolution signal decomposition:thewavelet representation[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1989,11(7):674-693.
[5]GOSWAMI JC,CHAN A K.小波分析理论、算法及其应用[M].许天周,译.北京:国防工业出版社,2007.
[6]郭健,孙炳楠.基于小波变换的桥梁健康监测多尺度分析[J].浙江大学学报:工学版,2005,39(1):114-118.(GUO Jian,SUN Bing-nan.Multi-scale analysis based on wavelet transform in bridge health monitoring[J].Journal of Zhejiang University:Engineering Science,2005,39(1):114-118.(in Chinese))
[7]何亮,敖鹏,孙炳楠.结构健康监测信息的多尺度分析[J].市政技术,2006,24(3):182-186.(HE Liang,AO Peng,SUN Bingnan.Analysis of information inmultiple measures for structurehealth monitoring[J].Municipal Engineering Technology,2006,24(3):182-186.(in Chinese))
[8]夏平,覃琴.基于多尺度分析的数字通信系统消噪[J].广西师范大学学报:自然科学版,2005,23(1):13-16.(XIA Ping,QIN Qin.Noise-filtering of digital communications systemsbased on wavelet multiresolution analysis[J].Journal of Guangxi Normal University:Engineering Science,2005,23(1):13-16.(in Chinese))
[9]陈飞,赵永,刘阳,等.多尺度分解在地震信号处理中的应用[J].中国地震,2004,20(4):405-409.(CHENFei,ZHAOYong,LIU Yang,et al.Application of wavelet on seismic signal processing[J].Earthquake Research in China,2004,20(4):405-409.(in Chinese))
[10]CHEN Y T,HO K C.Multi-resolution analysis,its link to thediscrete parameter wavelet transforms and its initialization[J].IEEE Trans Signal Processing,1996,44(4):1001-1006.
[11]DONOHO D L.De-noismg by soft-thresholding[J].IEEE Transaction on Information,1995,41(3):613-627.
[12]朱丽,娄国伟.自适应阈值的小波去噪研究[J].制导与引信,2003,24(1):13-16.(ZHU Li,LOU Guo-wei.Wavelet denoising study with adaptive threshold value[J].Guidance and Fuze,2003,24(1):13-16.(in Chinese))
