大坝监测信息的多维时空可视化
2010-10-11王佳林许后磊
杨 阳,王佳林,许后磊
(1.河海大学水利水电学院,江苏 南京 210098;2.河海大学水资源高效利用与工程安全国家工程研究中心,江苏南京 210098)
大坝及其监测信息可视为一个具有时空分布的多维动态系统,在整个工作运行的周期内,其自身结构性状及对外在因素的响应都会不断地发生变化.大坝安全监测[1]是确切了解这种变化以及分析和预测这种变化趋势的有效手段之一.全面的监测信息分析不仅可以保证大坝的正常工作以及坝体异常的及时发现和检修加固,而且可以提高大坝结构寿命评判的可靠性.固有的安全监测方法是一种简单的将某几个测点的数据及环境量罗列成表成图,再加以分析输出的方法.随着水利建设的发展,各种高坝会越来越多,高坝往往监测仪器数量多、类型复杂,监测数据量大、时空分布广.固有的安全监测方法很难满足多维度大容量数据分析的需要,更不利于人们去发现数据内在规律,分析评判坝体结构状态.
相对于数值和文字等符号信息,人对图片和色彩等形象信息的理解和感知效率更高,可视化正是据此用图像色彩来充分表现信息.可视化运用计算机图形学、图像处理技术、计算机辅助设计、计算机视觉及人机交互技术,将海量数据转换成图形和图像显示,从空间三维及时间维度去体现信息[2].信息可视化技术较早应用于地理信息系统[3],并取得了较好的应用效果,而在大坝监测领域,这种技术的应用还处于探索阶段[4-5].如何将大容量和多类型的大坝监测信息在多维空间上以多种视图灵活可变地表现出来,是一个亟待解决的问题.为此,笔者通过Matlab语言编写代码,对不同的大坝监测信息进行统一化处理,以时空上的场量表现这种信息,并应用人机交互技术实现图示的变换、缩放及查询功能,最终实现了大坝监测信息的可视化.
1 可视化类型
大坝信息包括大坝监测信息、坝体结构形状、监测仪器分布形式及监测类型,其中大坝监测信息是大坝信息的核心信息.依据大坝信息的特点,可将大坝信息分为3类:(a)大坝数字信息,即坝体及外部环境数字信息,包括降雨量、温度、水位、坝体状态参数及坝体内部监测数据等信息,这些信息描述了大坝的数值特征;(b)大坝空间信息,包括坝体空间几何形状、河谷地貌形态、基础结构及上下游河道几何参数等信息,这些信息描述了大坝的三维空间特征;(c)大坝时间信息,即时间维度下各个参数的变化情况,包括浇筑完成时间、首次蓄水时间和运行期加固、洪水和地震等发生的时间,这些信息从时间上反映了大坝的重大事件及坝体性状的突变情况.大坝监测信息的多维可视化是基于这3类信息的可视化,是将其以多维空间图示化的方式紧密结合、宏观表达、形象体现的信息集成和知识表达手段.
2 可视化内容和表现形式
根据大坝监测过程,可将大坝监测信息产生、采集和分析过程描述为:大坝在自身和外在环境的影响下,坝体结构性状发生变化,监测仪器将这些信息以数值方式提取出来,并通过计算分析还原为表征坝体状态的信息.这一过程可视为一条监测信息链(图1),在这条信息链上,监测数据和数据计算分析的结果是表征大坝和监测仪器状态的关键信息,是可视化的主要内容,而大坝和监测仪器是监测信息的物质基础,是可视化的次要内容.
大坝监测按类型可分为变形监测、渗流监测、内部应力应变监测和环境量监测4种[6-7].大坝监测所使用的仪器主要有正倒垂、引张线、视准线、渗压计、量水堰、测缝计、钢筋计、温度计、应力计、应变计、多点位移计和雨量计等,这些仪器一般分布于坝体内部廊道、坝基、坝身和坝体表面.根据仪器类型和测点位置,又可将监测信息分为2种:(a)描述大坝上下游、左右岸及竖直向的向量信息;(b)记录温度、体积、湿度、流速等非方向性的标量信息.
根据监测仪器的分布形式,可将信息可视化图形分为平面测值图、坝体多个剖面的空间测值云图和等值线图、结构三维空间云图.按照监测信息时间点的不同,赋予信息动态变化过程,还可形成包含时间因素的多维时空可视化动态图.

图1 监测信息链Fig.1 Monitoring information chain
3 可视化方法
3.1 空间离散测点的连续化
由于坝体测点布局一般根据监测类型、监测目的和仪器性能人为设定,其空间分布呈不规则离散状态,某些重要位置测点多,有些测点只分布在某一环线或平面上,因此难以按照等间距空间的统一算法对测点进行差值连续化处理.为此,采用Delaunay三角剖分算法[8]将离散的测点集合剖分成不均匀的三角形网格,如图2所示.
Delaunay三角剖分得到的三角形网格具有2个重要特性:(a)空圆特性,即在Delaunay三角形网格中,任一三角形外接圆范围内不会有其他点存在;(b)最大化最小角特性,即在散点集可能形成的三角剖分网格中,Delaunay三角剖分所形成的三角形的最小角最大.从这个意义上讲,Delaunay三角形网格是“最接近于规则化”的三角形网格.如果上述2个重要特性存在,则三角剖分算法具有如下3个优良属性:(a)最接近性,即以最临近的三点形成三角形.该属性可保证空间任意测点只与最临近的测点相关以及数据的准确性.(b)唯一性,即不论从区域何处开始构建,最终结果都是一致的.该属性可保证连续化数据的稳定性以及重复剖分数值的唯一性.(c)区域性,即新增、删除、移动某一个测点时只会影响临近的三角形.该属性可保证监测仪器的增减仅对局部产生影响.
3.2 监测数据的内插
较常用的数据内插方法有线性插值、样条插值和最临近插值方法等,这些插值方法难以适应不同测点因位置不同产生的几何位置变化,当测值分布不均或不规则时易产生插值精度不高或使得插值图形边缘退化图形模糊.为了保证插值的连续性以及对不同网格形状的适应性,这里参照有限元计算网格剖分方法[9],内插计算采用形函数插值算法.在空间数值的内插计算中,用2个三角行组成四边形,按照测点不规则的空间分布形式形成棱柱或六面体,并用其来拟合坝体结构,由于形成单元的不规则性,用等参单元加以描述(图3).图3(a)为不规则形单元,可按等参单元规则转换为图3(b)所示规则形单元,转换方法如下:
空间某点P的测值向量VP可表示为
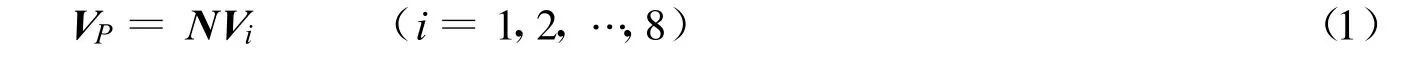
式中:V i——第i点的测值向量;N——依据测点空间坐标得到的形函数矩阵.在空间六面体八节点单元中,N的元素可表示为

图2 三角剖分网格Fig.2 Triangular meshes
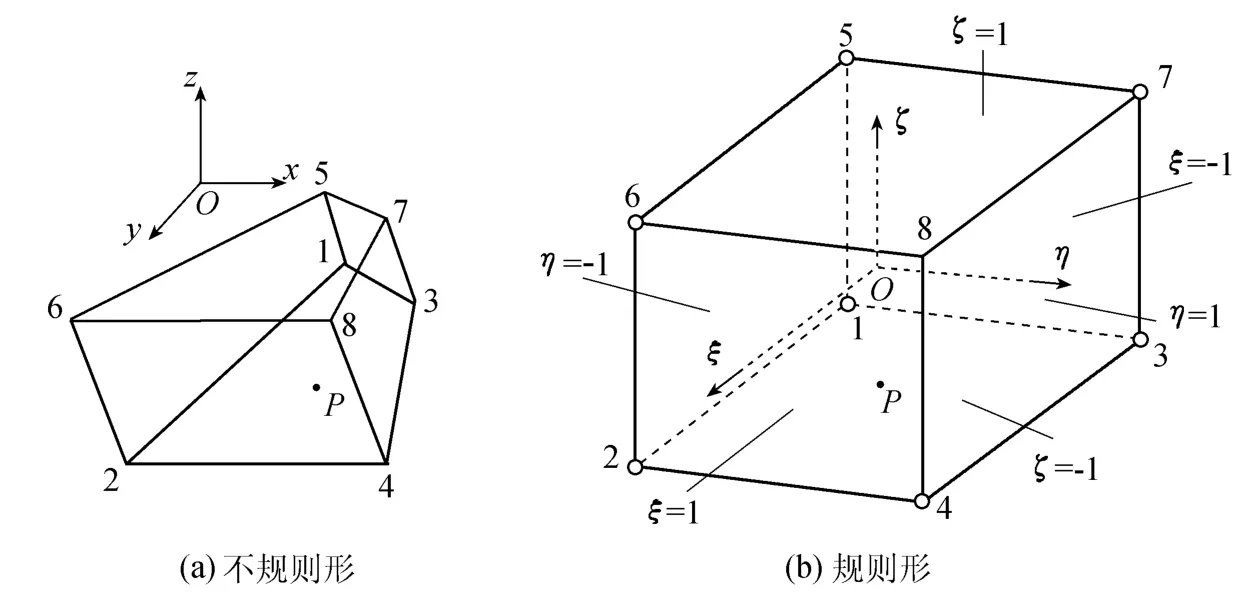
图3 空间八节点等参单元Fig.3 Eight-node isoperimetric elements
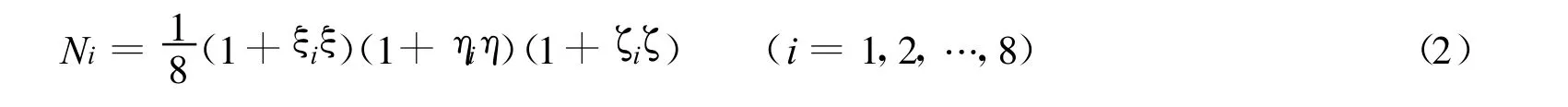
式中:ξi,ηi,ζi——i的母单元坐标;ξ,η,ζ——点 P 的母单元坐标.插值计算时先将 xyz坐标轴下的不规则单元用形函数转换为等参单元,再按式(1)计算P点测值,若 VP为与坐标轴有关的空间向量,则再用等参单元将 VP转换为原始坐标系下的测值.空间棱柱是空间六面体的简化,可参照有限元形函数[9]进行内插计算.平面数值内插是空间数值内插的简化,采用平面三角形单元的形函数进行内插计算,即令 i=1,2,3,可直接按式(1)进行计算.
3.3 流程及算法
流程为:(a)提取数据信息并分类;(b)进行整编计算及监测数据的连续化处理;(c)绘制坝体三维空间图以及监测信息的三维空间云图和等值线;(d)大坝监测信息时间维度上的显示变换等.根据流程利用Matlab软件[10]及其图像处理工具箱中的一些函数编写算法.算法所用到的一些主要函数及其功能如下:PLOT3(X,Y,Z,C)函数,用于绘制三维空间多段线,X,Y,Z分别为空间3个方向的点坐标集合矩阵,C为绘制线的形式和颜色;MESH(X,Y,Z,C)函数,用于绘制空间曲面;PATCH(X,Y,Z,C,inf)函数,用于绘制空间面片;pcontour(n,C,pxyz,tri,value)函数,用于绘制空间上测值相等的点,可在空间上形成任意曲面的等值线图,tri为使用delaunay函数划分出的三角形编号矩阵,n为等值线个数,C为等值线颜色,这里设置C=‘white',即等值线为白色;set(colorbar('vert'),'YTick',yTick,'YTickLabelMode','Manual','YTickLabel',Label)函数,colorbar(色带)控制三维空间场中,场量数值与云图颜色的对应关系.
4 可视化实例
4.1 大坝监测项目和仪器布置概况
本文以福建省境内某碾压混凝土重力坝为例来说明大坝监测信息可视化效果.该坝最大坝高115.0m,坝顶高程179.0m,由左至右共分为7个坝段.主要建筑物表面和内部布置了变形、渗流、温度、应力应变等监测项目.变形监测项目主要是坝体上下游、左右岸和垂向变形监测,渗流监测项目主要是坝基扬压力、坝体渗漏量和绕坝渗流监测,温度监测项目主要是坝体内部温度及大坝表面温度监测.坝体应变计、应力计以及坝体和闸墩裂缝计用于大坝应力应变等内部监测.大坝监测项目设置较为齐全,监测仪器状态良好,能较全面地获取坝体各个方面的信息.
4.2 监测仪器空间分布的可视化
大坝2个主要剖面温度计、坝顶引张线及内部电水平倾角计空间分布如图4所示.从图4可知:坝顶布置了11条引张线,埋设点分别为EX1,EX2,…,EX12;坝体中部横向布置了9个电水平倾角计,分别为CL14,CL15,…,CL22;坝体2个主要剖面布置了58支温度计,一个剖面布置的温度计分别为T5,T6,…,T38,另一个剖面布置的温度计分别为T39,T40,…,T62.界面工具栏中可选择对空间布置图进行保存、动态旋转移动、缩放、标记修改等的交互功能.
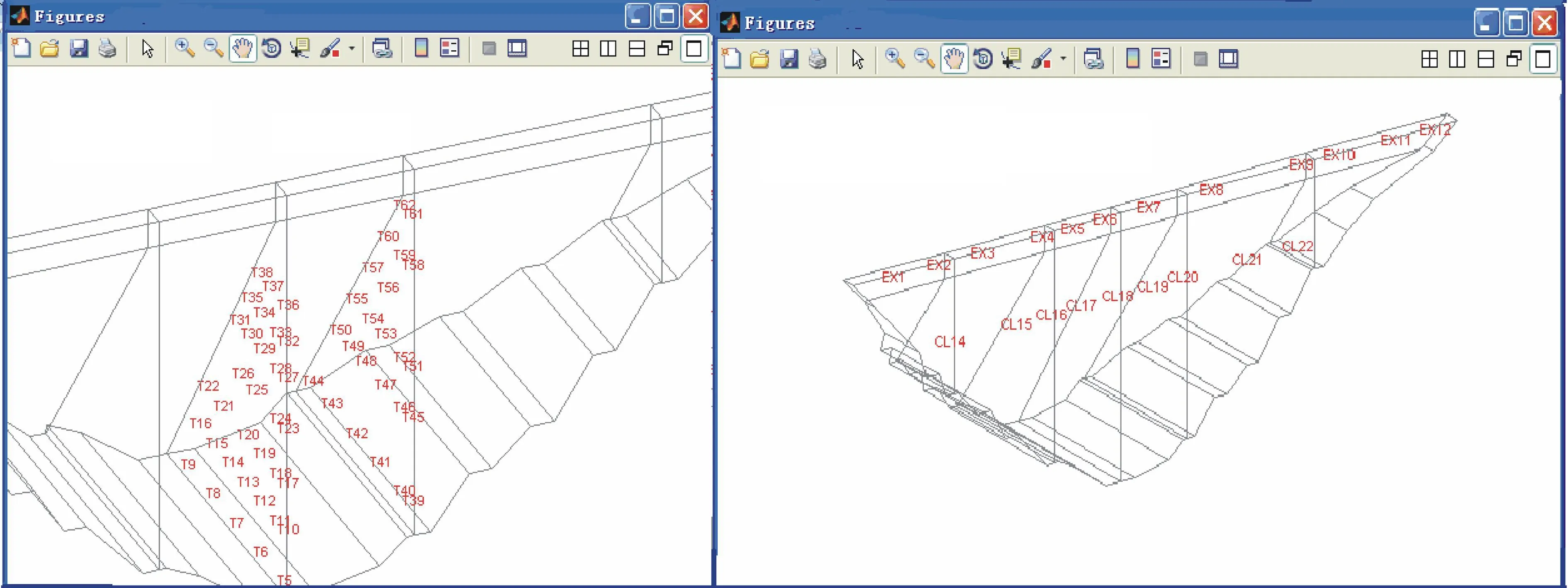
图4 监测仪器的空间分布Fig.4 Spatial arrangement of monitoring instruments
4.3 坝体位移场的可视化
利用大坝正垂线、倒垂线、引张线和视准线的空间监测数据绘制了大坝径向变形的空间位移场,如图5所示.图中网格表示大坝变形原始基准测值,实体部分表示变形后的空间效果.为了突出显示变形效果,将其放大了5000倍,云图显示了变形实际数值的大小.由此可见,大坝顶部中间变形超过4.93mm,这与实际情况相符.图5左下角滑块所指数字为07,表示该图显示的是大坝2007年初的监测数据,也可以拖动滑块动态选择2000—2009年初的监测数据.这里还可以平移、缩放、旋转空间视图,放大检查局部变形效果.点击自动动画效果图功能键,视图将从2000年逐年变换效果图直至2009年.
4.4 坝体剖面温度场的可视化
根据坝体2个主要剖面温度监测信息绘制了坝体剖面温度云图和等值线图,如图6所示.从图6可以看出,坝体内部温度高于外部温度,下游温度高于上游温度,下部温度低于上部温度.这种现象是由于蓄水期下游无水和坝体水深影响所致.

图5 坝体空间位移场Fig.5 Spatial displacement field of dam
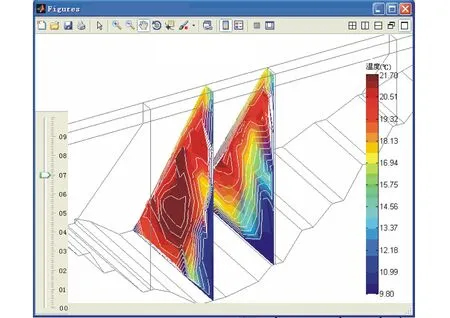
图6 坝体剖面温度场Fig.6 Temperature field of dam profile
5 结 语
本文基于可视化技术研究了大容量多维度大坝监测数据图形化方法,实现了空间测点数据的连续化和多维时空显示.通过多维时空显示,可以方便快速地发现数据集中隐藏的关系和模式,为大坝安全评定和坝体状态分析提供较为充分的依据.如何充分利用现有的可视化、空间三维动画及知识信息的融合等技术,实现大坝监测信息的远程采集、可视化分析、控制和可视化预警预测,最终建立一个完整的远程信息可视化分析控制系统,仍是有待研究的重要课题.
[1]吴中如.水工建筑物安全监控理论及其应用[M].北京:高等教育出版社,2003:1-9.
[2]栾春娟,侯海燕.创新研究国际前沿的可视化分析[J].科技与管理,2009,11(1):28-30.(LUAN Chun-juan,HOU Hai-yan.Visualization analysis on international frontiers of innovation studies[J].Science-Technology and Management,2009,11(1):28-30.(in Chinese))
[3]孙扬,封孝生,唐九阳,等.多维可视化技术综述[J].计算机科学,2008,35(11):1-7.(SUN Yang,FENG Xiao-sheng,TANG Jiuyang,et al.Survey on the research of multidimensional and multivariate data visualization[J].Computer Science,2008,35(11):1-7.(in Chinese))
[4]朱赵辉,顾冲时,包腾飞,等.基于可视化和组件技术的大坝安全监控系统软件研究[J].三峡大学学报:自然科学版,2007,29(6):486-489.(ZHU Zhao-hui,GU Chong-shi,BAO Teng-fei,et al.Study on dam safety monitoring system based on visualization and component technology[J].Journal of China Three Gorges University:Natural Sciences,2007,29(6):486-489.(in Chinese))
[5]李子阳,包腾飞,朱赵辉.基于TChart的大坝位移场可视化[J].河海大学学报:自然科学版,2008,36(4):496-500.(LI Ziyang,BAO Teng-fei,ZHU Zhao-hui.TChart-based visualization of dam displacement field[J].Journal of Hohai University:Natural Sciences,2008,36(4):496-500.(in Chinese))
[6]郭金根,李爱明.碾压混凝土大坝内部观测设计综述[J].大坝与安全,2002,36(6):16-18.(GUO Jin-gen,LI Ai-ming.Overview on internal monitoring design of compacted concrete dams[J].Large Dam and Safety,2002,36(6):16-18.(in Chinese))
[7]赵志仁,赵永.三峡工程安全监测设计的优化研究[J].水力发电学报,2005,24(6):53-56.(ZHAO Zhi-ren,ZHAO Yong.Optimization study on the safety monitoring design of the Three Gorges Project[J].Journal of Hydroelectric Engineering,2005,24(6):53-56.(in Chinese))
[8]DYER R,ZHANG H,MOLLER T.Voronoi-Delaunay duality and delaunay meshes[C]//ACM Symposium on Solid and Physical Modeling.New York:Association for Computing Machinery,2007:415-420.
[9]朱伯芳.有限单元法原理与应用[M].北京:中国水利水电出版社,1998:112-172.
[10]求是科技.MATLAB7.0从入门到精通[M].北京:人民邮电出版社,2006:2-15.
