求平面曲线渐近线的一种方法

丁雪梅

（曲靖师范学院 数学与信息科学学院，云南 曲靖 655011）

求平面曲线渐近线的一种方法

丁雪梅

（曲靖师范学院 数学与信息科学学院，云南 曲靖 655011）

根据曲线渐近线的定义，给出了求平面曲线渐近线的一种方法及其推广.

平面曲线；渐近线；方法

1 引言

如果一条曲线存在渐近线，我们就能知道这条曲线无限延伸时的走向及趋势，求出曲线的渐近线有利于我们研究曲线的变化情况.

定义1当曲线C上动点P沿着曲线C无限远移时，若动点P到某直线l的距离无限趋近于0，则称直线l是曲线C的渐近线[1].

曲线的渐近线有两种，一种是垂直渐近线，另一种是斜渐近线（包括水平渐近线）.若

或

则称直线x=a是曲线y=f(x)的垂直渐近线.据此，不难判别一条曲线是否存在垂直渐近线并将其求出.相对而言，斜渐近线较难求出，本文主要探讨斜渐近线的求法，给出一个定理及其应用并推广.

2 定理

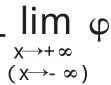
证明曲线y=f(x)上点(x,f(x))到直线y=k x+b的距离为

命题得证.

3 应用

解 因为

故直线x=0（即y轴）是曲线的垂直渐近线.

将函数f(x)改写为

又因为

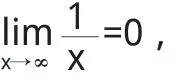
故直线y=x+2是曲线的斜渐近线.

解 因为

故直线x=-1是曲线的垂直渐近线.

将函数f(x)改写为

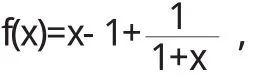
又因为

故直线y=x-1是曲线的斜渐近线.

解 因为

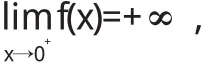
故直线x=0（即y轴）是曲线的垂直渐近线.

已知

且

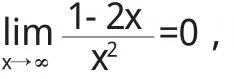
故直线y=1是曲线的水平渐近线.

例4求曲线f(x)=xarctanx的渐近线.

解 若将函数f(x)改写为

因为

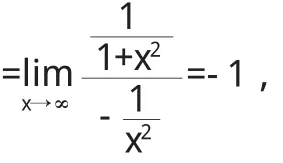
有

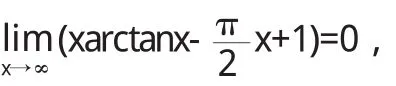
若将函数f(x)改写为

又因为

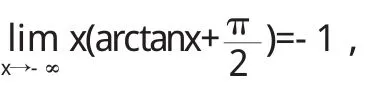
有

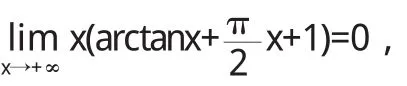
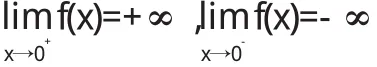
故直线x=0是曲线的垂直渐近线.

将函数f(x)改写为

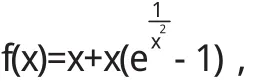
且

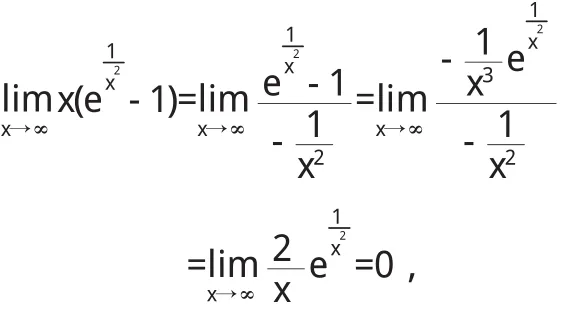
故直线y=x是曲线的斜渐近线.

解 因为

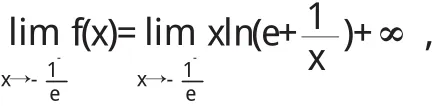
将函数f(x)改写为

又因为

有

4 推广

我们可以根据曲线的渐近线的定义，类似定义曲线的渐近曲线，并对定理1进行推广.

定义2若记两点P与Q之间的距离为d(P,Q)，定义点P到曲线C的距离为

定义3设有一曲线C,当曲线C上动点P沿着曲线C无限远移时，若动点P到某曲线Γ的距离无限趋近于0，则称曲线Γ是曲线C的渐近曲线.

解 因为

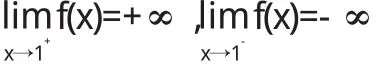
故直线x=1是曲线的垂直渐近线.

将函数f(x)改写为

又因为

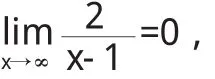
所以当x→∞时，函数f(x)的图像无限接近于抛物线y= (x-1)2.故曲线不仅有垂直渐近线x=1，还有渐近曲线y=(x-1)2.

〔1〕刘玉琏，傅沛仁，林汀，等.数学分析讲义（上册）（第五版）[M].北京：高等教育出版社，2008：309.

O174

A

1673-260X（2010）08-0003-02