同型平行机上的在线分批排序问题

卢文丽

（淄博师范高等专科学校 教育科学系，山东 淄博 255100）

同型平行机上的在线分批排序问题

卢文丽

（淄博师范高等专科学校 教育科学系，山东 淄博 255100）

排序；分批排序；竞争比；同型机；在线算法

1 引言

排序问题的理论与应用研究自二十世纪六十年代兴起以来，经过四十多年的发展已经成为组合优化领域的重要组成部分，被广泛应用到网络通信、自动化生产调度和物流管理等多个方面，从而使排序问题极具生命力和研究价值.

分批排序问题最早是在半导体集成电路制造的最后测试阶段预烧作业过程中提炼出来的一类重要排序问题，它是一种新型的排序问题，是经典排序问题的推广，在现代化生产的各个领域都得到了广泛的应用，随着大规模的现代化生产的发展，研究分批排序问题具有重要的实际意义.

分批排序问题可描述为：有固定的n个工件J1，J2，…，Jn需要在一台或多台批处理机上加工，每个工件Jj有工时pj、到达时间rj等，其到达时间和工时不一，要将工件分批加工.处理机一次最多能加工B个工件,工件加工过程中不允许被打断,也不允许移走或加入新工件.每一批的加工时间为属于该批的工件中最长工件的工时,开工时间应大于或等于该批中最晚到达的工件的到达时刻,且属于同一批的工件同时开工并同时完工.工件Jj的完工时间为所在批的完工时间，问题是如何合理地安排机器和工件，怎样分批，如何排序，使得某些要求（目标函数）达到最优，这就是所谓的分批排序问题.

由于分批排序问题具有较强的应用背景又是经典排序的推广，所以此类问题的研究工作于20世纪90年代以来很快得到发展并活跃起来.对于1|rj，B|Cmax的离线情形，1992年，C.Y.Lee等[1]在rj=0时给出了一些较基本的结果.Zhang和Deng[2]对具有不同到达时间情况的极小化加权总完工时间问题，给出了其N P完备性的证明，并给出了常数个到达时间和加工时间时的精确算法.

2 问题描述

在本文中我们研究同型平行机上的在线分批排序问题.其模型为：有m台速度相同的机器，现有n个工件不同时到达，假设工件的到达时间为rj，1≤j≤n，每个工件在到达前的信息都是未知的，只有到达后才能知道其所有信息，问怎样对工件进行分批，如何安排加工，使各批的最大完工时间尽可能的小.

本文我们将首次考虑更一般的问题pm|rj∈{0,r}，B|Cmax的在线问题，即所有工件有不同的加工时间，但只有两个到达时间的平行机在线分批排序问题.在给出算法之前先简单介绍相关符号的定义：

用J1，J2分别表示0时刻，r时刻到达工件的工件集，则J1∪J2即是所有工件的工件集.若用BLPT加工J1，则在最后一批工件完工时，各机器上的完工时间设为Ti1(i=1,2,…,m)，其=m a x{Ti1|i=1,2,…m}=Tk1；类似，若用BLPT加工J2，则所有工件完工时，各机器的完工时间为Ti2(i=1,2,…,m)，m a x{Ti2|i=1,2,…m}；若J1中部分工件与J2中工件，运用BLPT算法加工，则得到的最大完工时间记为.上述相应的最优排序分别记为C1*，C2*，；用C*表示本问题最优解；另外设pkt为用BLPT加工J1中，第k台机器上最后完工的工件.

3 算法描述

对于1|B|Cmax的离线情形,C.Y.Lee和R.Uzsoy[5]给出了一个多项式的FBLPT算法,且此算法是最优的.

FBLPT算法：

步骤1把工件按加工时间非增的次序编号使p1≥p2≥…≥pn；

步骤3任意安排各批的次序.

BLPT算法：

步骤2按pk非增的次序排列各批次序，当机器要出现空闲，就把排在前面的还未加工的批安排到这台机器上加工.

利用上述分批思想，我们对于pm|rj∈{0,r},B|Cmax的在线问题，给出了一个MBLPT算法.

MBLPT算法：

步骤1把J1中工件按BLPT算法进行分批，安排在各机器上加工；

步骤2若J2中工件在J1中所有工件都完工后到达，即，则用BLPT算法在r时刻开始加工J2；

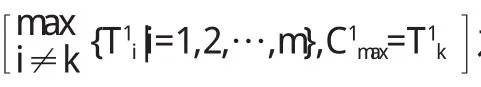
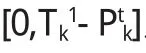
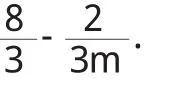
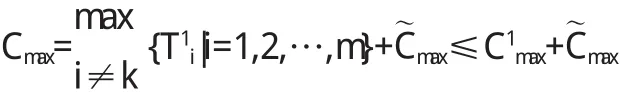
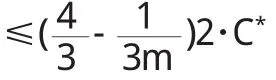
综上所述，定理成立.

根据以上分析，我们有下面的推论.

4 结论

〔1〕Lee C, Uzsoy R, Martin Vega. EfficienL algorithms for scheduling semiconductor buming operations [J]. Operations Research, 1992, 40: 764-755.

〔2〕Xiaotie Deng, Yuzhong Zhang. Miniming mean resposetime in batch progressing system [J]. Lecture Notes inComputer Science, 1999, 1627: 231-240.

〔3〕Zhang. G, Cai. X, C. K. Wong. On-line algorithms forminimizing makespan on batch processing machines [J].Naval Research Logistics, 2001, 48: 241-259.

〔4〕Zhang. G, Cai. X, C. K. Wong. Optimal on-line algorithmsfor scheduling on parallel batch processing machines[J]. IIE Transaction, 2003, 35: 175-181.

〔5〕C. Y. Lee, R. Uzsoy. Minimizing makespan on a singlebatch processing machines with dynamic job arrivals [J].IJPR, 1999, 37: 219-236.

O223

A

1673-260X（2010）03-0017-02