巨尾桉与青杨热学参数影响因素的实验研究

刘 昊,高建民,张璧光

(北京林业大学木材科学与工程北京市重点实验室,北京 100083)

0 引 言

木材的热学性质参数主要包括导热系数、导温系数、比热等。这些参数在木材干燥中十分重要。例如预测木材所需的预热时间[1,2]、研究木材干燥中温度场和湿度场的时空分布、建立干燥模型等。由于木材种类繁多、结构复杂,常用的就有几百种,对木材热学参数的测试工作量巨大,以及木材行业对木材热物性测试不够重视等多方面原因,导致绝大多数木材的热学性质参数都是一片空白。

中国林业科学研究院木材工业研究所和东北林业大学曾采用热脉冲法对国产55种木材的气干材在室温时的导热系数做了测定[3]。Suleiman等人认为木材导热系数是一个随其物理性质变化的非线性函数[4],文献[5]对压缩木材的导热系数进行了研究,文献[6]建立了木材导热系数在不同燃烧阶段的计算模型,文献[7]研究了木材导热系数在高温范围内的变化[7]、通过分型理论建立了木材横纹导热系数的理论模型[8],文献[9～14]结合木材物理学、统计热力学、物理力学等学科各自从理论上推导了多个关于木材热学参数的理论表达式。但是由于木材的微观机理和组成结构极为复杂,不同树种间差异较大,各理论计算公式针对具体树种在不同含水率下的导热系数的精确度有待提高。桉树和杨树是我国重要的人工林种[15,16],其木材产品有极高的经济价值。桉木和杨木的干燥是目前木材干燥界的热点之一,基于弥补其热学参数空白、推导出适用经验公式以及对不同阔叶材树种间进行比较的目的,本实验选择了尾巨桉和青杨作为实验材料。

1 材料与方法

1.1 实验材料

本实验选用巨尾桉 (拉丁名:Eucalyptus grandis×E.urophylla)广林9号和青杨 (拉丁名:Populus cathayana)为研究树种。

1.2 试验设备

(1)恒温恒湿箱:型号LHS-100CH

(2)准稳态导热性能测定仪:哈尔滨工业大学功达实验设备公司B型

1.3 试验方法

将原木去皮后锯截为板材,经过恒温恒湿箱干燥后将每块板材制成4块100 mm×100 mm×15 mm上下表面光滑的试件,为一组,试件分为径向试件和弦向试件。将试件放入准稳态导热性能测定仪中,打开电源开关,开始测试,进入准稳态后通过自带软件可得出试件导热系数和比热。实验均是在室温下进行。测试结束后利用烘干法对试件进行绝干处理,计算出本组试件的初含水率。

2 结果与分析

2.1 影响导热系数的因素

2.1.1 含水率对导热系数的影响

图1(a)、(b)分别为桉木和杨木在不同含水率下径、弦向导热系数的曲线图。从图中可以看出,导热系数与含水率成曲线关系,随着含水率的增加,径、弦向的导热系数都明显增大。其中含水率10%时的导热系数只有60%时的一半左右。这是因为热流在木材内部是通过其实体物质和孔隙来传递的,水的导热系数远大于空气,随着含水率增加,木材中部分空气被水所取代[3],从而导致导热系数的增大。而含水率在30%以上时,随含水率的增加导热系数增大幅度加快,这是因为纤维饱和点以上木材中增加的水分是以自由水的形式存在于细胞中。从图1a和图1b的对比中发现在相同含水率下,桉木导热系数比杨木平均大10%左右,这是因为实验中桉木的绝干密度 (437.11 g/m3)大于杨木的绝干密度 (387.33 g/m3)。在相同含水率下,绝干密度大的树种内部的实体物质相对较多,孔隙相对较小。孔隙中空气的导热系数远小于木材实体物质[3],因此在同含水率下绝干密度大的树种导热系数相对较大。

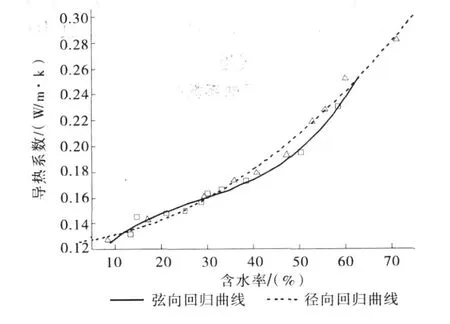
图1 a 不同含水率下桉木弦、径向导热系数曲线图Fig.1 a The radial and tangential thermal conductivity of Eucalyptus as a function of moisture content

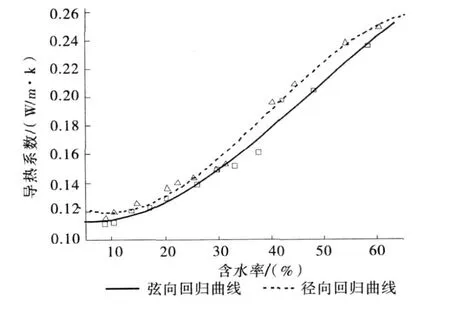
图1 b 不同含水率下杨木弦、径向导热系数曲线图Fig.1 b The radial and tangential thermal conductivity of Populus cathayana as a function of moisture content

Kollmann[17]认为木材横纹导热系数和和含水率的关系为

Maclean[17]提出的方程为

当W＜40%时,λ=0.020 5+ρ0(0.172 4～0.003 47 W)(kcal/m◦h◦℃);当 W ＞40%时,λ=0.020 5+ρ0(0.172 4～0.003 47 W)(kcal/m◦h◦℃)。式中ρ0为木材绝干密度。

表1是桉木和杨木在不同含水率下径、弦向导热系数的回归方程。与现有公式对比后发现,桉木在含水率 8%～40%的区间内,数值与Maclean方程比较接近,在含水率40%～70%之间,实验值介于Maclean方程和Kollmann方程值之间。杨木在含水率40%以下时数值略小于Maclean方程和Kollmann方程,40%以上时介于Maclean方程和Kollmann方程值之间,其中径向值与Maclean方程值接近。

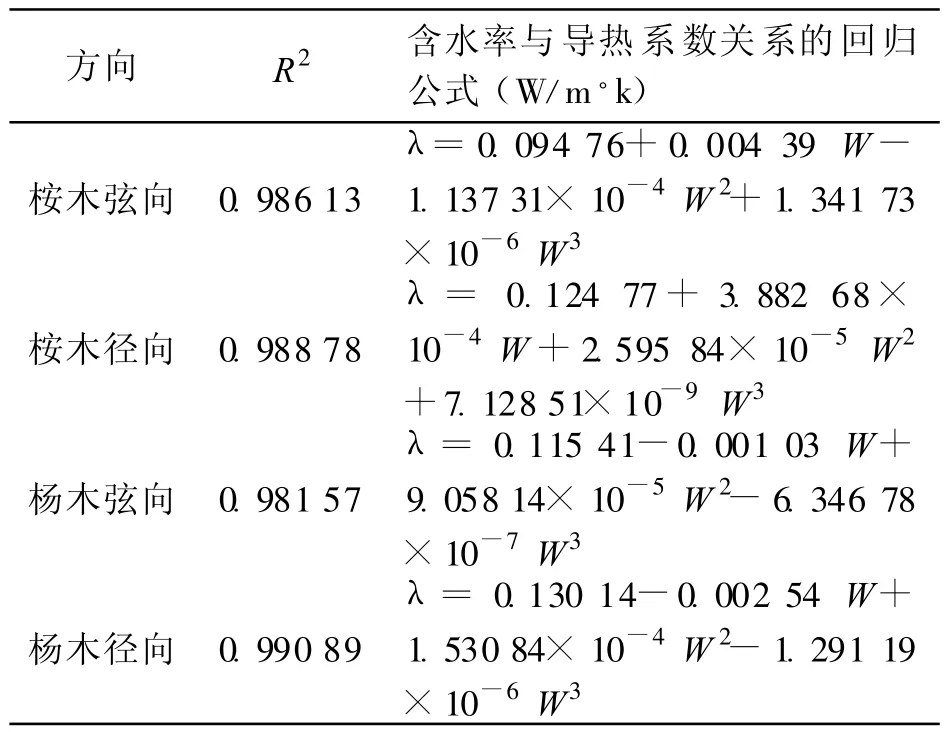
表1 含水率与导热系数关系的回归方程Tab.1 Empirical equation of thermal conductivity as a function of moisture content by regression analysis

2.1.2 纹理方向对导热系数的影响

从图1(a)上看出,含水率在27%以下时,桉木径向导热系数与弦向非常接近。而在27%～70%的区间内,径向导热系数明显大于弦向,二者最大差异在10%左右。从图1(b)中可以看出,杨木的径向导热系数比弦向大5%～10%左右。这是因为实验中测得的含水率是试件的平均含水率,在干燥过程中通过木射线传导的水分较多。由于木射线垂直于弦向而平行于径向,干燥过程中厚度方向上弦向干燥速度大于径向,因此干燥后在试件的厚度方向上径向所含水分略大于弦向,导致径向导热系数大于弦向。另外,含水率较高时差异比较明显,这是因为在高含水率下上述水分含量差异越大所致。

2.2 影响比热的因素

通过对比发现,在相同含水率下,桉木和杨木,径向和弦向间比热没有明显差异。图2是含水率与比热之间关系的曲线图。从图上可知,比热与含水率成曲线关系,随含水率的增加显著增大,其中含水率10%时的比热约为60%时五分之三。这是因为水的比热大于全干材比热,因此随着含水率的增大,木材比热也随之增大。比热与含水率之间关系的回归公式为 С=1.473 75+0.048 08 W-6.130 6×10-4W2+3.490 85×10-6W3(kJ/kg◦K)其中 R2=0.987 29。同Κ ИΡ ИЛО В[18]提出的在 M=10%～150%,t=20～100℃范围内,比热容经验公式为CM=进行对比的结果表明,含水率在25%以下时,回归曲线值略小于经验公式值,二者最大差异约为5%左右。含水率在25%以上时回归曲线值大于公式值,且随含水率增加二者差异增大,在含水率60%时二者差异为10%左右。

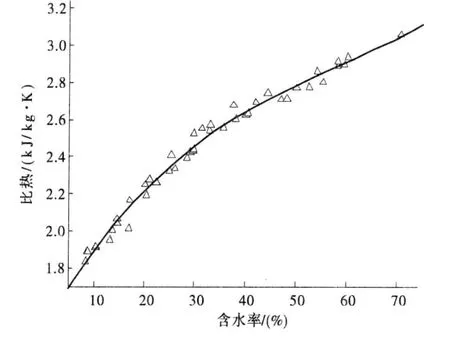
图2 含水率与比热关系曲线图Fig.2 The specific heat as a function of moisture content

2.3 影响导温系数的因素

2.3.1 含水率对导温系数的影响

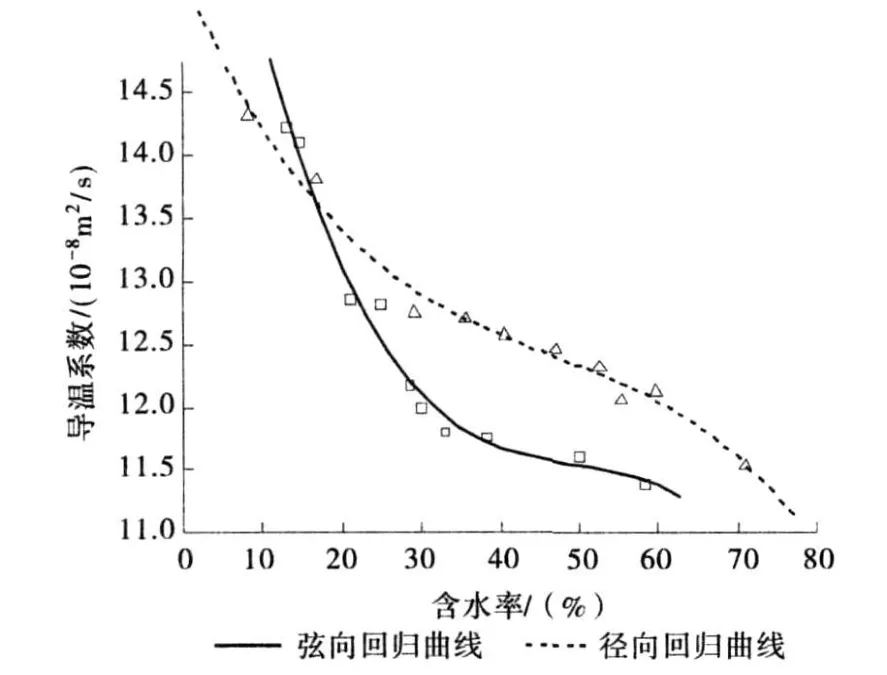
图3a 不同含水率下桉木弦、径向导温系数曲线图Fig.3 a The radial and tangential thermal diffusivity of Eucalyptus as a function of moisture content

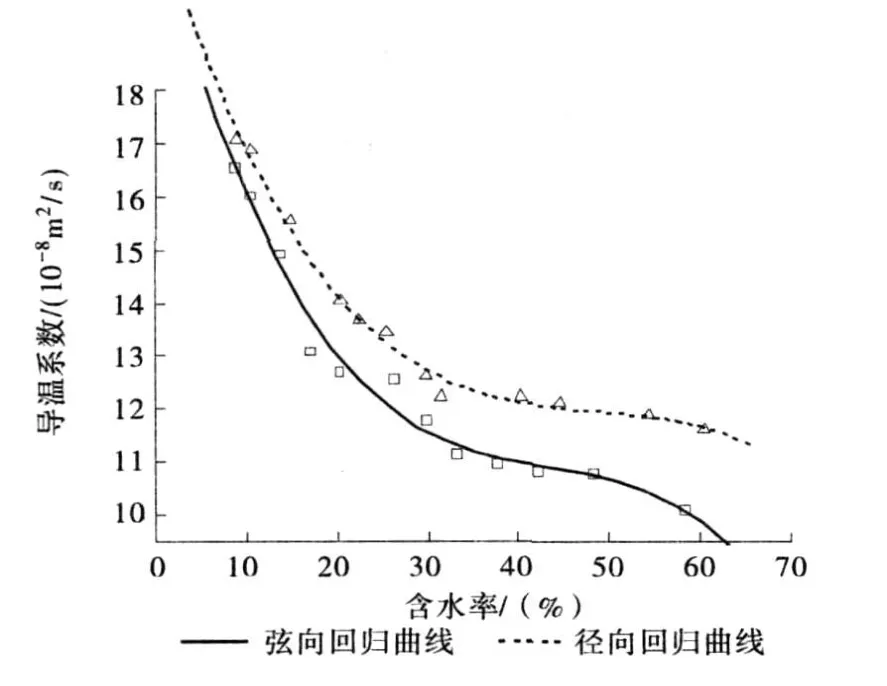
图3b 不同含水率下杨木弦、径向导温系数曲线图Fig.3 b The radial and tangential thermal diffusivity of Populus cathayana as a function of moisture content

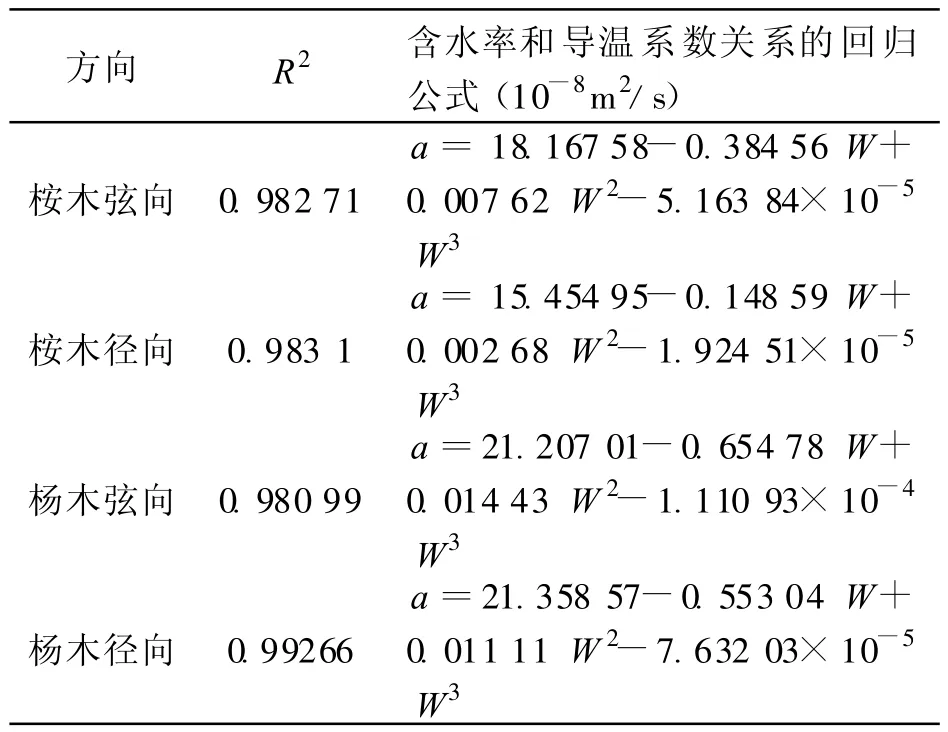
表2 含水率与导温系数关系的回归公式Tab.2 Empirical equation of thermal diffusivity as a function of moisture content by regression analysis

3.3.2 纹理方向对导温系数的影响

由图3(a)、(b)可以看出,杨木在整个曲线以及桉木在含水率在17%以上时,径向导温系数大于弦向导温系数,二者最大差异在10%左右,这是因为径向导热系数大于弦向,比热不受纹理方向的影响,因此求得的导温系数径向略大于弦向。

3 结论与讨论

(1)巨尾桉和青杨的热学性质参数受含水率、纹理方向的影响,其中含水率起关键作用。随含水率增加,导热系数、比热增大,导温系数减小。在纤维饱和点以上,含水率的增加使导热系数的增加速度加快。纹理方向上,导热系数和导温系数均是径向略大于弦向,但是比热不受影响。

(2)巨尾桉导热系数在相同含水率下高于青杨10%左右,这是因为巨尾桉的绝干密度大于青杨。二者比热没有差别。

(3)现有公式的计算值与实验值存在一定差异。本实验中导热系数、比热回归公式的相关度均达到0.98以上,可用于实际计算。

(4)本实验仅从含水率和纹理方向两方面对热学性质的影响进行了探讨,温度、密度、孔隙率等对其热学性质的影响尚需进一步研究。另外,针对回归公式的准确度需要进一步对其进行验证。

[1]李贤军,张璧光,杨涛,等.木材干燥预热时间初探[J].北京林业大学学报,2004,26(2):90-93

[2]刘新有,张璧光,伊松林.高温条件下木材升温时间的理论计算和实测[J].木材工业,2009,23(2):16-18

[3]刘一星,赵广杰.木质资源材料学[M].北京:中国林业出版社,2004.

[4]Suleiman B M,Larfeldt J,Leckner B,et al.Thermal conductivity and diffusivity of wood[J].Wood Science and Technology,1999,33(6):465-473.

[5]Asako Y,Kamikoga H,Nishimura H,et al.Effective thermal conductivity of compressed woods[J].International Journal of Heat and Mass Transfer,2002,45(11):2243-2253.

[6]Thunman H,Leckner B.Thermal conductivityof wood-models for different stages of combustion[J].Bi-omass and Bioenergy,2002,23(1):47-54.

[7]俞自涛,胡亚才,洪荣华,等.温度和热流方向对木材传热特性的影响[J].浙江大学学报(工学版),2006,(01)20-26.

[8]俞自涛,胡亚才,田甜,等.木材横纹有效导热系数的分形模型,浙江大学学报(工学版),2007,(02)

[9]陈瑞英,谢拥群,杨庆贤,等.木材横纹导热系数的类比法研究[J].林业科学,2005,(01).

[10]陈同英,杨庆贤.木材径向热导率的理论公式[J].应用科学学报,2003,(02).

[11]林金国,陈瑞英,杨庆贤.类比法研究木材径向导热系数[J].生物数学学报 ,2005,(02).

[12]林铭,陈瑞英,杨庆贤,等.木材弦向导热系数的类比法研究[J].集美大学学报 (自然科学版),2004,(04).

[13]杨庆贤.木材热学参数的理论表达式[J].福建林学院学报,2001,(04)

[14]杨庆贤.木材导温系数的理论表达式[J].福建林学院学报,2001,(02)

[15]杨时桐.尾巨桉木材的开发利用探讨[J].福建林业科技,2008(03)

[16]方升佐.中国杨树人工林培育技术研究进展[J].应用生态学报,2008(10)

[17]成俊卿.木材学[M].北京:中国林业出版社.1985.489

[18]尹思慈.木材学[M].北京:中国林业出版社,1996.