二维前视声纳阵列的幅相误差计算方法
2010-09-30陈志强
陈志强
(中国科学院声学研究所,北京100190)
二维前视声纳阵列的幅相误差计算方法
陈志强
(中国科学院声学研究所,北京100190)
二维前视声纳是一种基于二维阵列的采用空间谱估计技术探测前方目标和海底地形的声学设备。传统的基于特征根的波达方向估计方法需要阵列协方差矩阵以及一个精确阵列几何形状、幅度、相位等信息。但是由于声纳阵制造工艺的原因,实际的声纳阵各阵元具有一定的幅度不一致性和相位不一致性,影响了波达方向估计的性能。文中提出了一种利用阵列协方差矩阵的特性和自校正方法来对二维阵列的幅相误差进行联合计算的方法,它可以估计出每个阵元的幅相误差随入射角变化的曲线,改善波达方向估计的性能。
二维前视声纳;幅相误差;阵列协方差矩阵
1 引言
在阵列信号处理中,基于特征根的波达方向估计方法会产生很高的分辨率和准确的目标回波估计,但是这种方法对各种形式的阵列误差非常敏感,如阵元方向图误差,阵元通道幅相误差,阵元互耦以及阵元位置误差等因素,它会使得阵列流型产生一定的偏差,从而导致DOA算法性能急剧下降。因此在应用前需要得到阵列的幅相误差,从而进行校正,以获得最好的DOA估计性能。
因为幅相误差的存在,前人也提出了一些有效的幅相误差计算方法。Lo和Marple提出了一种需要方位已知的校正信源,因此这种方法不是一个真正的自校正计算方法[4]。Paulraj和Kailath提出了一种未知阵列幅度相位情况的自校正计算方法[5],这种方法不需要一个方位精确的校正源,但是仅限于均匀一维线阵。
本文所研究的二维前视声纳是一种均匀平面阵,通过二维DOA技术得到声纳阵前方空间的二维声像。由于不采用波束形成技术,每个基元的幅相误差较大,严重影响DOA估计性能。
基于上述背景,本文提出了一种二维均匀面阵的幅相误差计算方法。该方法将有源校正计算和自校正计算这两种方法结合起来,利用不同位置已知粗略方位的辅助信源对二维均匀阵列幅相误差进行计算,并通过计算机仿真证明了该方法的有效性。
2 阵列信号处理模型
假设有一M×N(6×6)元二维均匀面阵见图1,存在方位依赖的幅相误差,两个方向的相邻阵元间距都为d(一般为半个波长)。有一个窄带点源以平面波入射,入射角为(φ,θ),波长为λ。则不存在阵列误差时,均匀面阵的导向矢量为:

其中以第一个阵元为参考阵元。当阵元存在幅相误差时,导向矢量为:

式中:为阵元幅相扰动矩阵;ψk为第k个通道的幅度误差;φk为第k个通道的相位误差。如果以第一个阵元为参考阵元,可以认为ψ1=1,φ1=0。
阵列接收到的信号为:
X(t)=a'(φ,θ)S(t)+N(t)t=1,2,…,L(3)式中:S(t)为信号矢量;N(t)为噪声矢量;L为快拍数。

图16 ×6均匀等间隔面阵
3 二维前视阵列幅相误差计算方法
对于二维前视声纳的测量一般会在水池中进行,可将二维前视声纳安装在二维回转机构上,将测试使用的信源放置在远场区域,利用旋转机构可以造成二维前视声纳接收不同入射角的信号。但是二维初始角度的绝对值很难确定准确,因此利用旋转机构的等间隔特性可使阵列逐个接收二维多个不同的入射角的信号。利用得到的信号通过MUSIC算法以及一维重复拟合的方法可以得到精确的二维初始入射角。之后便可以得到幅相误差。大体步骤如下:
(1)得到二维不同入射角度的采样数据矩阵;
(2)利用接收信号自相关矩阵的局部Toeplitz性估计各角度对应的幅度误差;
(3)用得到的幅度误差校正原有的阵列流型;
(4)利用MUSIC算法估计幅度误差校正后的各个入射角度;
(5)固定某一个方向,通过一维最小二乘法得到另外一个方向的初始角度;
(6)等间隔旋转固定的方向N次,对同上得到的N个初始角度取平均;
(7)通过上述方法得到的数据同理也可以得到另外一个方向的初始角度;
(8)利用自校正方法以及二维初始角度从而估计各个角度对应的相位误差。
具体流程框图如图2所示:

图2 二维阵列幅相误差计算流程框图
3.1 初始入射角的估计方法

对于不同的入射角方向分别采集得到采集数据矩阵Xp,快拍数为L。
(b)利用面阵的局部Toeplitz性估计每个方向的幅度误差矩阵Ψˆp,具体算法见下小节。
(c)用得到的每个方向的幅度误差校正理论的阵列流型:
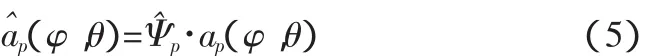
其中ap(φ,θ)为第p个方向的理论导向矢量。


(f)按照以上方法,每得到一个初始俯仰角的估计值,就等间隔旋转Δφ,φ方向共测量Q个点(要在初始角度做一个标记,以便于每次在θ方向旋转一周后还可以回到原来θ方向的初始角度)。即得到等Q个θ方向的初始角度估计,那么:


即为所求初始角(φ¯0,θ¯0)中的θ¯。
3.2 阵列幅相误差计算方法
(1)阵列幅度误差估计方法
方法:利用二维均匀面阵的接收数据协方差矩阵的局部Toeplitz性
对于某一个入射角度(φ,θ),设阵列幅度误差矩阵为Ψ,相位误差矩阵为Φ,它们均为M×M维的对角阵(M为阵元个数),设
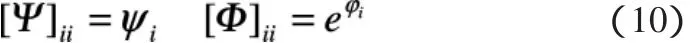
则

当不存在误差时,信号协方差矩阵为:

考虑误差后的信号协方差矩阵P为:

其中Ψ=ΨH,ΦHΦ=I,Φ-1=ΦH
对上式两边取模(因为|φii|=1)有:

对于均匀线阵阵列的情况,R满足完整的Toeplitz性质,当i-j=k-l时,|[R]ij|=|[R]kl|,而对于面阵的情况,由于导向矢量的复杂性,不再满足Toeplitz性。但是通过计算可以发现,面阵阵列的R满足局部Toeplitz性,当i-j=k-l时,只有很少一部分|[R]ij|≠|[R]kl|,而大部分情况仍然满足|[R]ij|=|[R]kl|,利用这种局部近似性质仍可以得到:
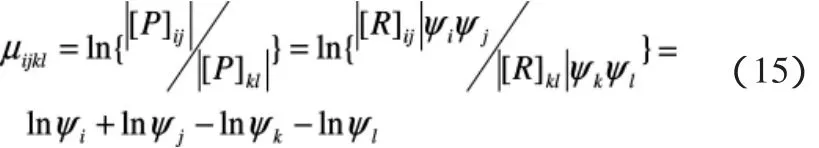
对于所有满足i-j=k-l的元素共形成含有个线性方程组。
设B是一个的k×M维的矩阵,B[lnψ1,lnψ2,...,lnψm]T=[...,μijkl,...]T,通过简单的矩阵运算可以得到[lnψ1,lnψ2,...,lnψm]T=,其中B#为B的伪逆。
即可求出幅度误差:Ψ=exp(Ψ)(16)
实际幅度误差与估计幅度误差的仿真结果见图3所示。

图3 幅度误差比较示意图
(2)阵列相位误差估计方法
方法:利用自校正计算方法



其中w=[1,0,...,0]T是一个M×1维的向量。最终的相位误差为:

实际相位误差与估计相位误差的仿真结果见图4所示。

图4 相位误差比较示意图
4 仿真研究与分析
下面通过仿真来验证上述应用于二维前视声纳的幅相误差计算方法的有效性。仿真中采用6X6的均匀面阵,阵元间距为半波长,发射信号为单频信号,频率为150 kHz,快拍数为400。假设远场有一个信源,因为二维前视声纳水平角度的范围为[-45,45],俯仰角度范围为[45,135],设其初始方位角为[42.3,127.7],首先给其二维均匀面阵的每个阵元加一个幅度误差和相位误差,生成入射信号,令信噪比为20 dB。
4.1 测量计算二维前视声纳幅度和相位的误差曲线
将被测换能器安装在一个回转机构上,初始角度设为[42.3,127.7],固定初始角度中水平角42.3°不变,以后每次等间隔旋转俯仰角5°,记录面阵所接收到的信号,重复上述操作,共测量和记录15个位置的数据。之后把初始角度的俯仰角转回初始位置。等间隔旋转水平角5°,按此方法,共等间隔旋转水平角14个位置,共接收14×15=210个数据。每个位置可以通过上述计算幅相误差的方法得到不同阵元的幅相误差。
图3 、图4为[32.3,122.7]时面阵的每个阵元的真实幅相误差与估计幅相误差的比较。由以上210个不同角度位置数据计算可得:幅度误差的均方根平均值为0.008 3。相位误差的均方根平均值为0.024 5。
4.2 初始角度的计算方法
初始角度为[42.3,127.7],通过上面介绍的多次一维拟合求均值的方法,可以得到估计的初始角度[42.367 3,127.749 8],水平初始角度的拟合曲线如图5,俯仰初始角度的拟合曲线如图6。

图5 水平初始角度拟合曲线示意图
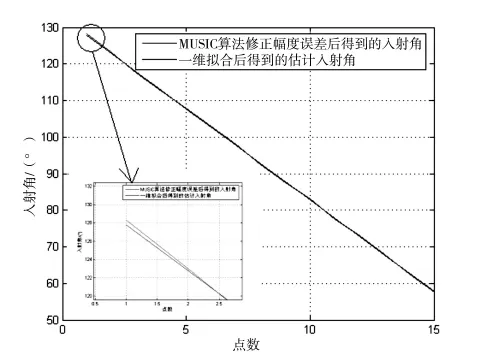
图6 俯仰初始角度拟合曲线示意图
5 结论与展望
本文提出了一种应用于二维前视声纳的阵列幅相误差计算方法。研究是基于二维前视声纳的原理和特点进行的,它具有下述特点:一是幅相误差由多种形式的误差组成,无法单一地采用某种误差的计算方法,二是阵列的幅相误差是随入射角变化的,不是一个恒值。三是基于面阵的导向矢量的特点。通过实验仿真,取得了很好的测试结果,通过此方法可以得到阵列的幅相误差曲线。该方法特别适用于高频二维水声换能器面阵。
[1]B Ottersten and M Viberg.Local modeling and robust estimation for high-resolution direction finding.in Proc 25th Asilomar Conf Signals,Systems,and Computers,(Pacific Grove,CA),Nov 1991,1005-1009.
[2]叶根.一种应用于水声换能器线阵的幅相误差校正方法[D].中国科学院研究生院硕士学位论文,2009.
[3]B Friedlander and A J Weiss.Eigenstructure methods for direction finding with sensor gain and phase uncertainties.ICASSP,New York,1988,2681-2684.
[4]J T-H Lo and S L Marple.Eigenstructure Methods for Array Sensor Localization.ICASSP,Dallas,Texas,1987,2260-2263.
[5]A Paulraj and T Kailath.Direction of arrival estimation by eigenstructure methods with unknown sensor gain and phase.in Proc ZCASSP’85 Aug.1985,640-643.
Abstract:Planar forward sonar is an acoustic equipment which explores underwater landform and physiognomy using DOA technology in planar array.Direction of arrival estimation using eigen-structure methods requires knowledge of the array covariance matrix and an exact characterization of the array in terms of geometry,sensor gain and phase.If the method is applied with incorrect sensor parameters,the method essentially breaks down or gives poor results.A new approach which uses information in the observed covariance matrix and self-calibration to correct the errors is proposed.Finally,the accuracy source directions and array gain and phase errors curve can be estimated.The method doesn't need many hypotheses and will lead to the better performance.
Key words:planar forward sonar;gain and phase error;covariance matrix
Array Calibration Method with Unknown Sensor Gain and Phase for Planar Forward Sonar
CHEN Zhi-qiang
(Institute of Acoustics,Chinese Academy of Sciences,Beijing 100190,China)
TB566
A
1003-2029(2010)02-0039-04
2010-03-15
国家高技术研究发展计划-海洋环境立体监测技术资助
陈志强(1985-),男,北京人,中国科学院声学研究所硕士研究生,研究方向为信号与信息处理。Email:zhiqiang_chen1@126.com
项目(2006AA09Z119)
