隧道洞口段结构地震响应分析
2010-09-27严松宏张巧慧
苏 惠,贾 良,严松宏,张巧慧
(1.陕西铁路工程职业技术学院 铁道工程系,陕西 渭南714000;2.兰州交通大学土木工程学院,甘肃兰州730070)
隧道的进出口是隧道唯一的暴露部分,是整个隧道抗震设防的薄弱环节。隧道洞口所处的地质条件,多为严重风化的堆积体,覆盖层较薄,容易造成山体失稳,产生滑动和坍塌。大量的地震灾害表明,地震对浅埋隧道、偏压隧道、明洞及洞门的影响较大。在地形、地质条件不利的地段,当发生强烈地震时,常由于滑坡、地表开裂、断层位移等造成洞口堵塞、洞门开裂、衬砌变形等不同程度的破坏[1]。因此,在隧道和隧道洞口位置选择及具体设计时,应考虑地震烈度、地形和地质条件,特别是地形陡峻的不良地质对隧道的影响。
本文运用结构动力分析计算方法和ANSYS软件中瞬态动力分析[2]的功能,研究了地震荷载作用下围岩材料的渐变对隧道洞口段抗震性能的影响。
1 计算方法
采用Newmark隐式积分预估修正算法求解运动平衡方程[3]。有限元体系在t+Δ t时刻的运动平衡方程为

式中:M为体系的总质量矩阵;C为体系的总阻尼矩阵;K为体系的总刚度矩阵;+Δt为体系的节点加速度向量;+Δt为体系的节点速度向量;ut+Δt为体系的节点位移向量;Ft+Δt为外荷载向量为单元应变矩阵;为单元应力向量。
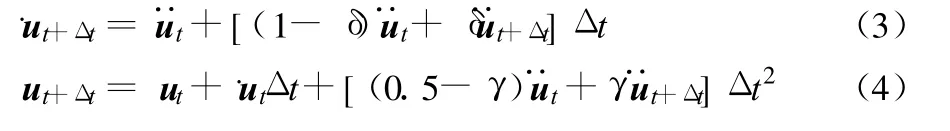
Newmark方法采用下列假设:式中:δ、γ为积分常数,分别取为0.5、0.25。Newmark隐式积分法是无条件稳定的。

体系的总阻尼矩阵采用瑞利阻尼式中:α、β为常数,可分别按两种不同的振动频率下测得的阻尼比ξ加以确定[4]。
2 有限元模型的建立
隧道进口段位于右江南岸低山丘陵区,洞身埋藏较浅,埋深约20 m。岩体较破碎,节理及裂隙发育。起迄里程为DK11+970~DK13+585,全长1 565 m。文章选取定造隧道洞口DK11+970~DK12+050段。计算范围为:长×宽×高=80 m×60 m×55 m。采用8节点三维等参数单元solid45以及弹簧单元combin14,共划分单元总数27 156,节点总数29991。隧道结构体系有限元模型如图1所示。为研究围岩参数的变化对隧道地震响应的影响,选取了5组不同的围岩[5],围岩物理力学参数见表1。边界条件为:底面、两个侧面和后侧设置粘-弹性人工边界,前侧为自由边界。围岩材料沿隧道轴向的分布情况见图2,计算工况见表2。
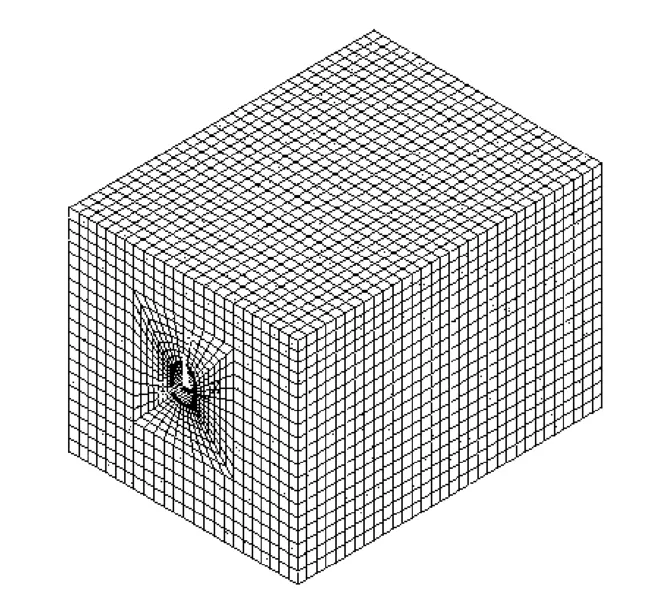
图1 隧道结构体系有限元网格模型

表1 材料物理力学参数
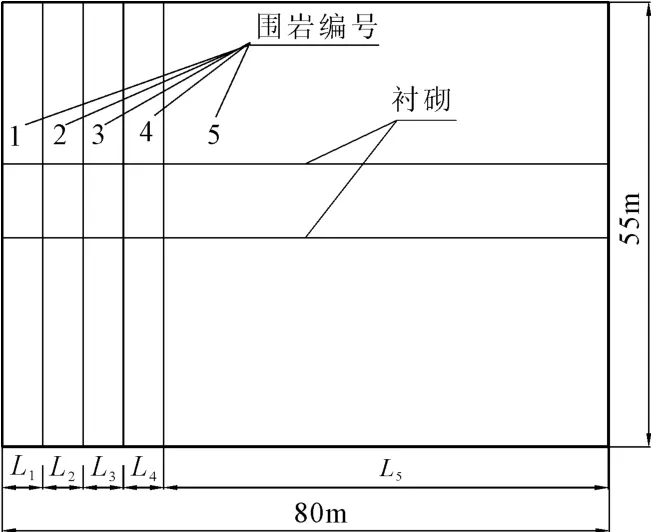
图2 围岩沿隧道轴向的分布情况
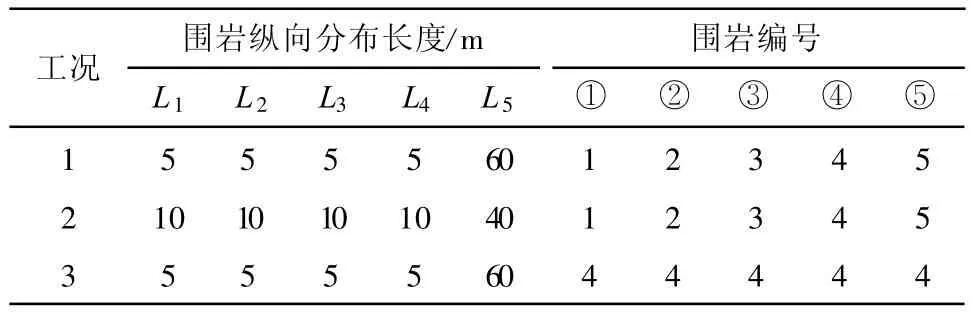
表2 计算工况
本文选取EL-Centro[6]水平8度地震波为地震输入。地震波(震级M=7.1,震中距50 km,最大加速度NS分量为3.42 m/s,持续时间30 s)的前10 s加速度记录作为输入的地震荷载,如图3所示。

图3 EL-Centro地震加速度南北分量记录曲线
3 计算结果与分析
3.1 衬砌关键部位应力结果分析
图4~图6为各工况下沿隧道轴线方向衬砌边墙脚处最大应力变化曲线。从图4、图5中可以看出,不论洞身段围岩为围岩5或围岩4,对于洞口段分布着地质条件差的围岩,即计算中洞口段围岩是由软弱向较硬的围岩逐渐变化时,洞口段衬砌的应力显著的增大。从图6可以看出,对于未考虑洞口段围岩分布逐渐变化的情况,即洞身段围岩与洞口段围岩相同的情况,洞口段衬砌应力与洞身段衬砌应力基本相同。

图4 工况1-沿隧道轴线方向衬砌边墙脚最大应力变化曲线

图5 工况2-沿隧道轴线方向衬砌边墙脚最大应力变化曲线
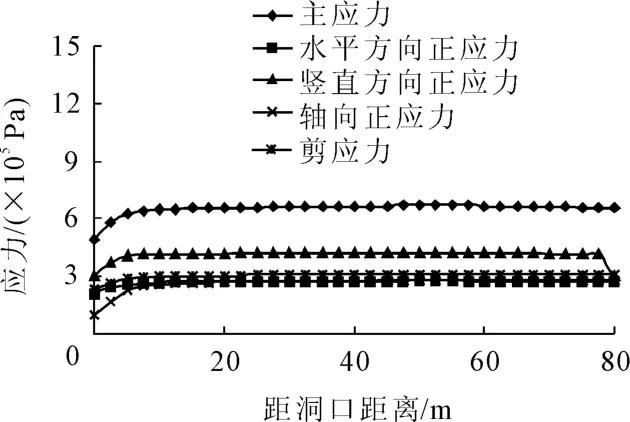
图6 工况3-沿隧道轴线方向衬砌边墙脚最大应力变化曲线
对照图4和图5可见,洞口段围岩由软弱向较硬的围岩逐渐变化的长度越长,洞口段衬砌应力就越大,洞口段设防长度就越长;图4中围岩渐变段长度为20 m,而图5中围岩渐变段长度为40 m,后者洞口段衬砌最大主应力约增大了42%左右;当洞口围岩渐变段长度为20 m时,衬砌最大应力发生在距洞口15 m处左右,距洞口30 m以后衬砌应力才逐渐减小,所以此时洞口段抗震设防长度选取30 m比较合适,当洞口围岩渐变段长度为40 m时,衬砌最大应力发生在距洞口27.5 m处左右,距洞口50 m以后衬砌应力才逐渐减小,所以此时洞口段抗震设防长度选取50 m比较合适。由此可见洞口段设防长度与洞口段围岩性质是有很大关系的。
3.2 衬砌关键部位位移结果分析
图7为不同工况下沿隧道轴线方向衬砌拱顶最大位移变化曲线。从图中可以看出,工况1和工况2洞口段围岩是由软弱向较硬的围岩逐渐变化的,围岩由洞口越向洞内延伸,位移越小;工况1和工况2最大位移均发生在洞口,工况1最大位移为6.36 mm,工况2最大位移为9.14 mm,后者最大位移约增大了30%左右;工况3洞口段围岩是均质的,没有发生渐变,位移曲线趋于平缓。因此加强洞口位移的检测可以进行加固长度的控制[7]。

图7 各工况下沿隧道轴线方向拱顶最大位移变化曲线
3.3 衬砌关键部位加速度结果分析
图8和图9分别为工况1中洞口衬砌拱顶以及与拱顶相邻的围岩加速度时程曲线。从图中可以看出两者很形似,因此可以认为在8度水平地震荷载作用下,围岩和结构的相互作用不大[8,9],也就是衬砌结构的动力破坏可能性是较小的。

图8 衬砌拱顶加速度时程曲线
4 结论与建议
(1)洞口段围岩由软弱向较硬的围岩逐渐变化时,洞口段衬砌各关键部位的应力均呈现先增大后减小的趋势,洞口段围岩由软弱向较硬的围岩逐渐变化的长度越长,洞口段衬砌应力就越大,洞口段设防长度就越长,由此表明洞口段设防长度与洞口段围岩性质是有很大关系的;未考虑洞口段围岩分布逐渐变化的情况,即洞身段围岩与洞口段围岩相同的情况,洞口段衬砌应力与洞身段衬砌应力基本相同。

图9 围岩顶部加速度时程曲线
(2)洞口围岩渐变段长度为20 m时,抗震设防长度选取30 m较为合适;洞口围岩渐变段长度为40 m时,抗震设防长度选取50m较为合适。
(3)洞口段围岩由软弱向较硬的围岩逐渐变化时,围岩由洞口越向洞内延伸,位移越小,最大位移发生在洞口;当洞口段围岩是均质时,没有发生渐变,位移曲线趋于平缓。
(4)在8度水平地震荷载作用下,围岩和衬砌相互作用不大。
(5)隧道等地下结构的地震反应分析研究是一个复杂问题,影响因素很多,如地震波的选择和确定,边界条件的处理,地震波输入方式等,这些问题都有待于进一步的研究。
[1]潘昌实.隧道地震灾害综述[J].隧道及地下工程,1990,11(2):1-9.
[2]高峰,严松宏.隧道时程动力反应分析改进算法[J].岩石力学与工程学报,2003,22(7):1088-1092.
[3]高峰,关宝树.沉管隧道三维地震反应分析[J].兰州铁道学院学报,2003,22(1):39-43.
[4]高峰,李德武.隧道三维地震反应分析若干问题的研究[J].岩土工程学报,1998,20(4):48-53.
[5]潘昌实.隧道及地下结构物抗震问题的研究概述[J].世界隧道,1996,16(5):7-16.
[6]于泳波,万振江,刘健新.减震技术在公路桥梁中的应用及地震反应分析[J].长安大学学报(自然科学版),2004,24(2):58-60.
[7]SHARMA S,WILLIAN R J,雷谦荣.地震对地下洞室的破坏[J].地下空间,1992,12(4):335-344.
[8]许增会,宋宏伟.地震对隧道围岩稳定性影响的数值模拟分析[J].中国矿业大学学报,2004,33(1):41-44.
[9]蔡佳骏,李之达,易 辉,等.ANSYS二维弹塑性分析在联拱隧道围岩稳定性评价中的应用[J].水利与建筑工程学报,2005,3(1):10-14.
