城市固体废弃物填埋场边坡地震响应分析
2010-09-27李勇
李 勇
(茂名职业技术学院,广东 茂名525000)
自从1988年位于美国Kettleman山的一个垃圾填埋场发生失稳以后,填埋场的稳定问题开始引起人们的重视,在我国也发生过因填埋场失稳造成人员伤亡和地下水环境污染的实例[1]。美国的联邦法律(U.S.Federal Regulation)规定对于建在地震区的填埋场必须能够承受设计最大水平加速度的地震动,并给出了按照拟静力法进行地震分析时地震系数选取的简化方法。Bray J D(1998,2001)等采用非线性动力分析程序计算了地震作用下填埋场的非线性响应特性[2,3],对填埋场进行了地震响应计算。陈云敏等[4]基于极限平衡法,考虑水平地震力,得到了填埋场衬垫界面滑动的安全系数和屈服加速度系数的近似解。孔宪京等[5]开展了城市垃圾填埋场地震变形机理的振动台模型试验研究,这些研究成果为垃圾填埋场抗震设计奠定一定的基础。我国《城市生活垃圾卫生填埋技术规范》(CJJ17-2004)对新建填埋场的选址作了严格的规定[6],但是缺乏对填埋场抗震设计的具体规定。填埋场地震稳定分析一般采用传统的岩土边坡稳定分析方法,但与岩土边坡不同之处在于填埋场的边坡和库底具有复合衬垫系统,该系统可以阻止填埋体产生的渗滤液污染周边环境,但在地震荷载作用下,对于这种具有复合衬垫系统的边坡地震响应的研究成果较少。本文结合某城市垃圾填埋场工程实际,基于有限单元法进行二维地震动力响应分析,研究成果对填埋场抗震设计具有一定的指导和参考意义。
1 填埋场动力响应分析方法
在地震荷载作用下,填埋场表现出非线性动力特性,采用非线性分析方法对填埋场进行动力响应分析与填埋场在地震荷载作用下的工作性态具有较好的一致性。动力有限元控制方程为[7~9]:

式中:[M],[C],[K]分别为总质量矩阵、总阻尼矩阵和总刚度矩阵;{¨u},{﹒u},{u}分别为结点加速度、速度和位移列阵;{¨ug(t)}输入地震加速度列阵;[J]为各项地震动分量的指示矩阵。在采用瑞利阻尼的情况下,阻尼矩阵用下式表示[C]=α[M]+β[K],直接用数值积分方法求解方程(1)得到填埋场边坡动力响应。
2 地震动输入
由于缺乏工程所在地的地震记录,难以直接用当地地震记录作为本研究的地震动输入,为了充分反映填埋场边坡动力响应特性,本文选择人工波作为输入地震动进行地震动力响应分析,以反映地震动特性对填埋场地震效应的影响。图1为输入地震动时程曲线和频谱曲线。对于人工合成的地震波,能量主要集中在频率为3Hz~6Hz范围内。所选择的地震波的频谱和持时,具有一定的代表性,基本上能够反映地震荷载作用下填埋场的动力响应特性。
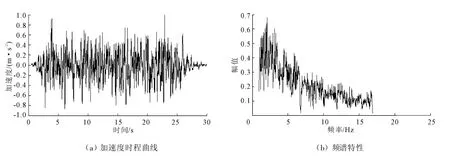
图1 人工合成地震波
3 填埋场动力稳定响应分析
某填埋场衬垫系统为厚度300 mm的厚粘土衬垫,衬垫上为300 g/m2的土工布,2.0 mm厚的HDPE光面防渗膜,HDPE土工膜之上铺设400 mm无纺土工布,无纺布之上铺设200 mm厚中粗砂保护层,中粗砂层上铺设300mm厚砾石层。衬垫系统如图2所示。计算模型如图3、图4所示。计算所需的垃圾填埋场基本计算参数见表1。
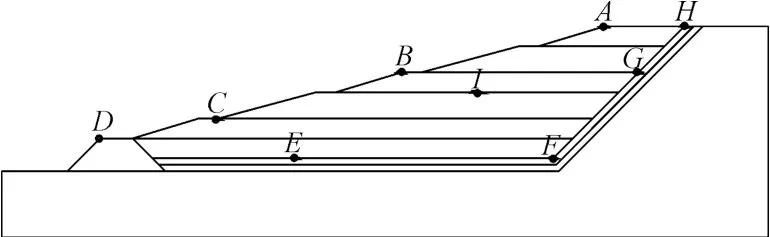
图2 衬垫系统及监测点布置
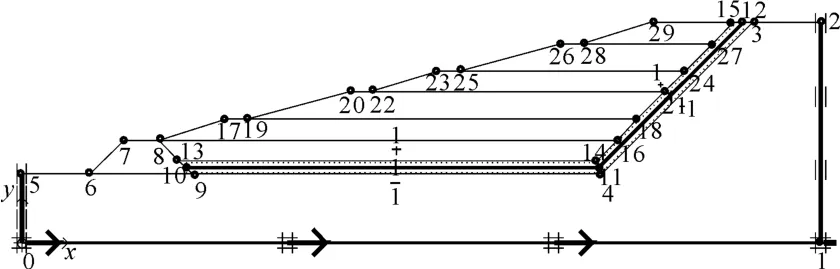
图3 某垃圾填埋场计算模型(有衬垫层)

图4 有限元计算模型(有衬垫层)
计算时采用弹塑性双曲线HSsmall模型。模型中包含独立刚度模量,能模拟垃圾土在10-5~10-3范围内的应力应变关系。HSsmall模型用垃圾土的应变历史参数及两个附加材料参数来表示,即G0和γ0.7。其中G0为小应变时的剪切模量,γ0.7为剪切模量衰减到70%时所对应的剪应变。当该模型用于动力分析时,包含了材料的粘滞阻尼。按照本文提出的计算方法,对某垃圾填埋场进行了地震响应分析。监测点的布置如图2所示。

表1 垃圾填埋场基本计算参数
3.1 衬垫层对边坡动力响应的影响
衬垫层是填埋场边坡与其它边坡不同的显著特性之一。为研究衬垫层对填埋场边坡动力响应的影响。在原模型基础上将衬垫系统去掉,然后进行有限元计算。计算模型如图5,图6所示。
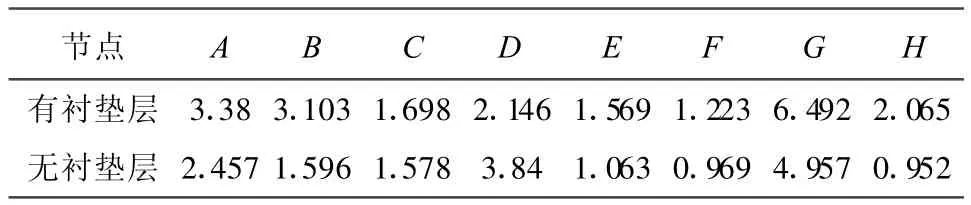
表2 有无衬垫层时节点的加速度峰值(m/s2)
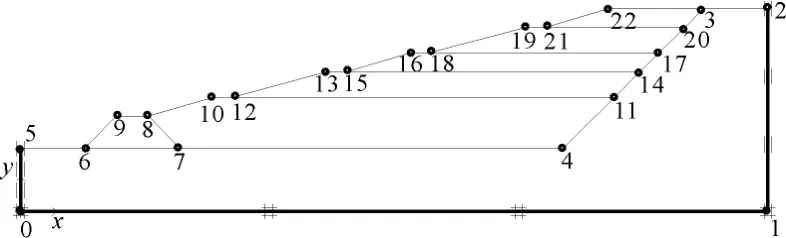
图5 某垃圾填埋场计算模型(无衬垫层)
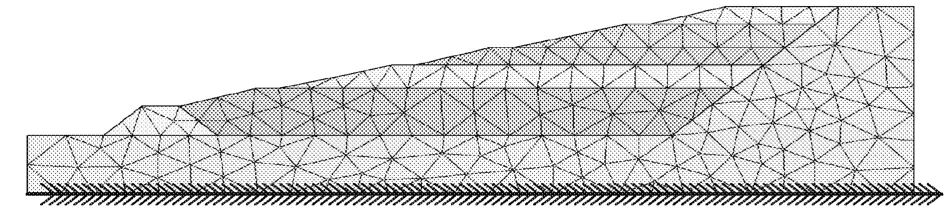
图6 有限元计算模型(无衬垫层)
表2为边坡有无衬垫层时各节点的峰值加速度,由图7可见,填埋场边坡地震反应中含有衬垫层的边坡峰值加速度均比无衬垫层时大,因此衬垫层的存在对边坡加速度有放大作用;衬垫层位置不同时对边坡加速度响应的放大作用不同,边坡上的衬垫层比填埋场底部的衬垫层对加速度响应的放大作用大,即图中节点G的放大效应比节点E的大。节点D是位于垃圾坝上的点,衬垫层的有无对其影响很大。衬垫层填埋深度不同对反应的频率特性影响也不同,衬垫层的存在,使土体频率减小,而衬垫层位置越深,土体频率越小。
3.2 本构模型对边坡动力响应的影响
为了研究不同本构模型对边坡动力响应的影响,在保证几何模型、材料、地震波数据等其它因素相同的情况下,选取EL波作用下坡顶(节点A)及底部防渗衬垫层(节点E)来进行分析,见图8、图9。

图7 有无衬垫层时各节点加速度峰值曲线

图8 节点A加速度响应时程曲线(左图:HSsmall模型;右图:莫尔-库仑模型)

图9 节点E加速度响应时程曲线(左图:HSsmall模型;右图:莫尔-库仑模型)
由图8、图9加速度节点时程曲线图可知,使用HSsmall模型所得最大加速度为0.047 m/s2,采用摩尔-库仑模型所得最大加速度为0.815 m/s2。莫尔-库仑模型作用下的加速度时程响应明显大于HSsmall模型。

表3 不同本构模型下的加速度峰值(m/s2)
由表3、图10可以看出,在不同本构模型作用下,各节点的加速度峰值有很大的不同。在莫尔-库仑模型作用下边坡体上加速度峰值明显比HSsmall模型大,而垃圾坝和边坡衬垫层在莫尔-库仑模型作用下的加速度时程响应整体都比HSsmall模型的小。
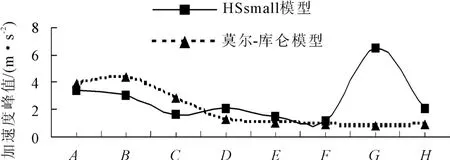
图10 节点加速度峰值曲线
4 结 语
本文基于动力有限元法,对某城市固体废弃物填埋场进行了二维非线性地震响应分析,为了反映填埋场边坡在不同结构形式和不同本构模型下地震动力响应的特性,经分析比较得到如下结论:
(1)衬垫层的存在会增大填埋场边坡动力响应;对加速度而言,在衬垫层处加速度峰值放大系数有突变,突变量较大。总体而言,衬垫层的存在对边坡动力响应影响较大。
(2)填埋场边坡在不同本构模型作用下,坡顶处的加速度时程响应趋于一致,且随着填埋深度的增加,都存在放大效应;两个模型的计算结果相差较大,与莫尔-库仑模型结果相比,HSsmall本构模型体现了土在动力作用下的特性,计算的结果更合理。
(3)由于填埋场为复合边坡系统,填埋场与岩土边坡相比更复杂,其动力响应与岩土边坡动力响应相比具有显著差异,应加强对填埋场地震动力响应特性的进一步研究。
[1]邓学晶,孔宪京.垃圾填埋场动力稳定机理及稳定分析研究现状与进展[J].世界地震工程,2007,23(4):59-61.
[2]Bray J D,Rathje E R.Earthquake-induced displacements of solidwaste landfills[J].Journal of Geotechnical Engineering,1998,124(3):242-253.
[3]Rathje E R,Bray J D.One and two-dimensional seismic analysis of solid-waste landfills[J].Canadian Geotechnical Journal,2001,38(3):850-862.
[4]陈云敏,等.垃圾填埋场沿衬垫界面的地震稳定性及永久位移分析[J].中国科学E辑:科学技术,2008,38(1):79-94.
[5]孔宪京,邓学晶.城市垃圾填埋场地震变形机理的振动台模型试验研究[J].土木工程学报,2008,41(5):65-74.
[6]CJJ17-2004.城市生活垃圾卫生填埋技术规范[S].北京:建筑工业出版社,2004.
[7]张国栋.基于反应谱的土与结构相互作用体系非平稳随机地震反应分析[J].振动与冲击,2005,24(4):31-34.
[8]董建华,朱彦鹏.地震作用下土钉支护边坡稳定性计算方法[J].振动与冲击,2009,28(3):119-124.
[9]彭伟,李建中.减隔震连续梁桥非经典阻尼问题与地震响应简化分析[J].振动与冲击,2009,28(1):146-151.
