一种改进的FDTD网格剖分算法
2010-09-27
(空军工程大学 导弹学院,陕西 三原 713800)
1 引 言
在采用时域有限差分(Finite Difference Time Domain,FDTD)方法对模型进行电磁场的数值计算时,先必须对所考虑的模型进行剖分。网格剖分的好坏,不仅影响到计算结果的精度,而且对计算过程的收敛程度起着决定性的作用,因而一种好的网格剖分算法对整个FDTD计算来说有着举足轻重的意义。网格的描述应符合电磁场的变化,如果在每个计算域中都用细网格来描述,势必要占用计算机过多的资源和较长的运行时间;如果在每个计算域中采用粗网格来描述,则将会给FDTD的计算带来较大的误差。为了解决这一矛盾,通常采用非均匀FDTD法[1-6]。文献[4]中介绍了一种使网格尺寸在空间按一定的规律扩展的非均匀网格法,其基本思想是使网格密度沿轴向按等比级数增大。这种网格生成的方法,由于在整个网格空间都是用等比级数的方式增长得到的,使得6个场分量的迭代式的一致性较好。李响等人[2]在扩展网格算法的基础上改进了分区扩展网格的算法,并在其编写的非均匀剖分软件中用到了分区递变的非均匀网格算法并实现了设置和剖分结果的可视化。周国祥等人[3]同样也以可视化的形式实现了非均匀网格剖分,提出了一种很具通用性的较合理的非均匀网格剖分算法,即分区递变结合粗网格的非均匀网格算法。
分区递变的非均匀网格剖分方法与一般的非均匀网格相比有了较大的改进,但也存在着一定的局限性:网格的最小尺寸和比例常数要人为设定;在算法处理的过程中,基本上是通过调整最小网格尺寸Δxmin及各网格的对应比例Rx使其能满足要求,此过程不但结果不好控制,而且可能会产生一些意想不到的结果。对于Δxmin及Rx如何进行适当的调整才能得到比较理想的结果,文献中并没有给出合理的方法。基于此算法的基本思想,本文提出了一种更加合理的网格自动生成的算法。
2 改进的分区递变非均匀网格剖分算法
首先,通过AutoCAD、3DMax等第三方绘图软件画出模型的立体图,以特定的格式将其导出;然后,通过程序将该文件读入,就可以得到此模型的结构,同时也可以得到模型在3个轴向上的分界面及不连续点的坐标。
以x轴方向为例,假设通过模型的读入,得到在x轴方向的一系列不连续点的坐标从小到大分别为x0,x1,x2,…,xn。依据媒质特性及所计算的频率范围,我们可以得到空间最大网格的尺寸Δxmax。依据Δxmax,取Δxmin=Δxmax/5,此精度一般可以满足计算中不连续点处的需要,过小则由于同时还要考虑到时间步的关系,使得时间步过小,要使得内部的场稳定必然增加所需要的时间步数,此值也依据实际情况手动设定。要保证计算空间场的稳定性,相邻的网格间的尺寸应该平缓地变化而不是突变,防止数值色散,为此,设定比例系数Rx≤1.3。
由于x0与xn处于计算空间的边缘,其网格将延展到PML层中,此处的网格作为第三种形式予以考虑。而中间由x1到xn-1之间的网格均属于由细网格到粗网格再到细网格的变化过程。
定义靠近分界点的网格均为最小网格Δxmin,以最大的比例系数1.3增大,直到达到最大网格长度Δxmax,由此可以求得以此规律增大可以得到的最大网格数ΔNmax及空间长度ΔLmax。而ΔNmax满足如下关系式:
(1)
即其增长所达到的最大尺寸小于保证在计算空间内收敛的最大值Δxmax,若继续增大将大于这一收敛条件。由此可以得到:
(2)
式中,LowI()表示对所求得的数向下取整,如LowI(9.2)=9。在得到ΔNmax后,可以求得按此规律得到的最大空间长度:
(3)
令ΔL=xi-xi-1(1 设当半区间网格数为n时,网格刚好达到或超过半空间长度ΔL/2,即: (4) (5) (6) n=LowI(ΔL/Δxmin) (7) 在此区间内可取Δx=ΔL/n。 定义除去两边的递增网格长度,中间剩余部分的总长度为ΔL′=ΔL-2ΔLmax。中间的网格长度均为Δxmax,网格个数为n,则有: n=UpI(ΔL′/Δxmax) (8) 边缘的网格由于此处不存在不连续性,故[x0,x1]区间为从x1向x0网格尺寸递增,而在[xn-1,xn]区间为由xn-1向xn网格尺寸递增。此区间一般大于3个网格,由于是单调递增,不存在双边网格数的问题,故此处只需考虑大于3个网格的情况。此处如果ΔL<ΔLmax,则按照中间网格小于Δxmax的方式进行单边带处理;如果ΔL≥ΔLmax,则按照中间网格大于Δxmax的方式进行单边带处理。 由以上3种情况可以得到整个x轴方向分区间在以上3种形式下的剖分算法,在y轴方向和z轴方向可以依据此算法进行同样的剖分。 根据以上算法,应用VC++编程对一个微带贴片天线和一个低通滤波器模型进行剖分,结果如图1~4所示。由图可以看出,在不同媒质的交界面和金属边界条件处网格都采用最小尺寸,这样在得到最小网格数的同时,最大限度地避免了网格尺寸所带来的数值色散。 图1 微带贴片天线Fig.1 Microstrip patched antenna 图2 剖分后的微带贴片天线网格Fig.2 The divided grids for microstrip patched antenna 图3 低通滤波器Fig.3 Lower-passed filter 图4 剖分后xy平面的网格Fig.4 The divided grids in xy plane 采用改进算法所得空间网格的尺寸,在整个空间区域内并不是简单的递增关系,这一特性使得空间网格不但能够避免数值色散,而且由于与一般算法相比其最大网格尺寸可取得更大一些,故其总的网格数相对其它算法来说也可以取得更少一些。同时,由于算法采用分区处理及递增网格与最大网格相结合的方法,既使小网格出现在场变化剧烈的区域,又保证了场变化缓慢的区域均为大网格。与普通的剖分算法相比,这种剖分算法可产生更少的网格数,大大缩短了计算时间。由于这种剖分过程完全可由程序自动完成,因而该算法可以很好地应用于各种非均匀FDTD网格剖分程序。 参考文献: [1] 高本庆. 时域有限差分法[M]. 北京: 国防工业出版社, 1995. GAO Ben-qing.Finite-Difference Time-Domain Method[M].Beijing:National Defense Industry Press,1995.(in Chinese) [2] 李响, 杨明武, 王伟吉,等. 时域有限差分电磁建模系统的研究与设计[J].信息与电子工程, 2005, 3(4): 257-260. LI Xiang,YANG Ming-wu,WANG Wei-ji,et al.Study of FDTD Electromagnetism Modeling System[J].Information and Electronic Eegineering,2005,3(4):257-260.(in Chinese) [3] 周国祥,程萍,蒋经国,等.直角坐标系下非均匀FDTD网格生成系统[J].微波学报,2005,21(2):56-59. ZHOU Guo-xiang,CHENG Ping,JIANG Jing-guo,et al. A Non-uniform FDTD Mesh Generation System in Cartesian Coordinate[J]. Journal of Microwaves, 2005,21(2): 56-59. (in Chinese) [4] 姚广锋,王积勤, 刘刚. 采用PML的FDTD方法对矩形微带天线的研究[J].现代雷达,2003,25(11):36-38. YAO Guang-feng,WANG Ji-qin,LIU Gang. A Study on the PML Absorbing Boundary Condition of the FDTD Method for Rectangle Microstrip Antenna[J].Modern Radar, 2003, 25(11):36-38. (in Chinese) [5] Reineix A,Jecko B.Analysis of Microstrip Patch Antennas Using Finite Difference Time Domain Method[J].IEEE Transactions on Antennas and Propagation,1989,37(11):1361-1369. [6] David M Sheen, Sami M Ali, Mohamed D Abouzahra,et al.Application of the Three-Dimensional Finite-Difference Time-Domain Method to the Analysis of Planar Microstrip Circuits[J].IEEE Transactions on Microwave Theory and Techniques,1990,38(7):849-857.2.1 中间网格值小于Δxmax


2.2 中间网格值等于Δxmax
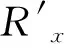
2.3 边缘网格
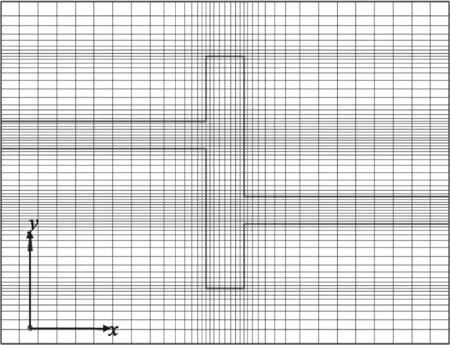
3 剖分实例



4 结 论
