相量法与傅里叶变换法的联系与区别*

党建亮 林爱英 朱连轩 吴丽丽 袁 超

河南农业大学 河南郑州 450002

相量法与傅里叶变换法的联系与区别*

党建亮 林爱英 朱连轩 吴丽丽 袁 超

河南农业大学 河南郑州 450002

论文主要分析了在“电路”与“信号与系统”课程中，相量法与傅里叶变换法两者之间的联系与区别。相量法和正弦稳态电路的分析、频率响应及零状态响应分析分别是各自课程中的重点及难点，对后续课程起着关键性的作用。文中通过实际例子详细分析了相量法与傅里叶变换法在求解频率响应方面的一致性，特别重点讨论了在求解系统零状态响应方面，学生容易误解而许多教科书也没有具体讲解到的两者之间的区别。

相量法；傅里叶变换；零状态响应

相量法是电路课程中的重点及难点,现有教材导出相量概念时或者直接利用欧拉公式或者通过数学变换的概念引出相量法,建立正弦量与相量的一一对应关系,还有一些文献引入新的变换建立了两者之间的联系。但在利用相量分析电路系统稳态响应方面都很少介绍与傅里叶变换的联系,然而在信号与系统课程中,分析电路系统的频率响应时,许多教材往往直接利用电路的相量法求解系统的频率响应,这就给学生造成了理解的困难：是否相量法与傅里叶变换法具有等价性？但两者各自的推导过程似乎毫无关联,有的教材也只是在介绍拉氏变换章节时简单地说明两者在一般情况下是等价的,于是有的文献讨论了相量法与傅里叶变换的关系,研究了两者之间的统一性。但这样又容易给学生造成误解,认为两者是统一的,实际上相量法与傅里叶变换法仅在分析系统频率响应时是一致的,而在求解零状态响应时是有区别的。以下给予具体的说明。

一、相量法与傅里叶变换法适用性的讨论

本文通过简单的例子详细讨论了相量法与傅里叶变换法在实际系统分析中的适用性，尤其重点分析两者在求解系统响应方面的区别，便于教师更好的讲解和学生更好的理解掌握。

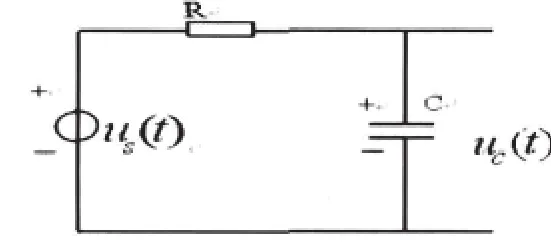
图1 例题电路图

1.求解系统频率响应的一致性

(1)利用相量法求解系统频率响应。由电路图可知，输出电容电压相量与输入电源电压相量之比即为该系统频率响应，利用电路分压定律得：

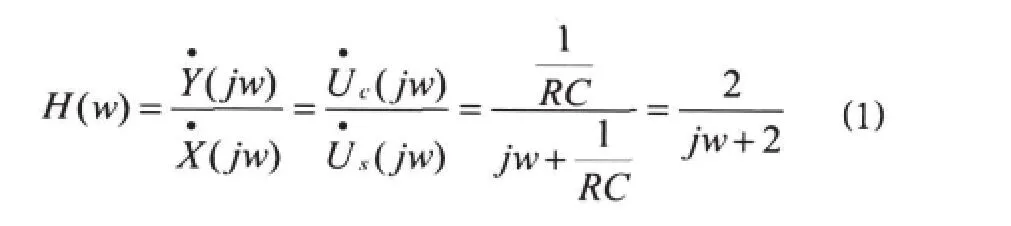
(2)利用傅里叶变换法求解系统频率响应

根据电路图1列出电路方程式：

两端进行傅里叶变换得

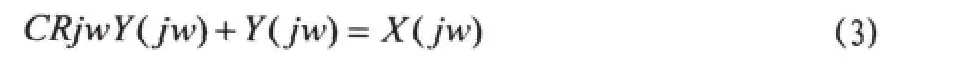
解得频率响应为

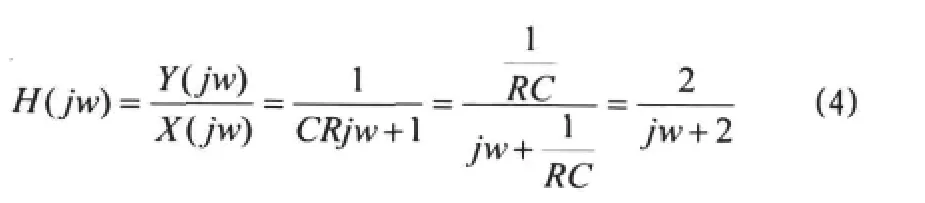
由结果可知两种方法求解频率响应是一致的。

2.求解零状态响应的不一致性：

(1)利用相量法求解系统的零状态响应

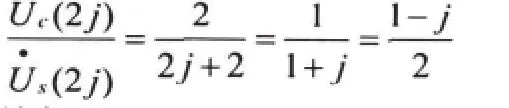
故得

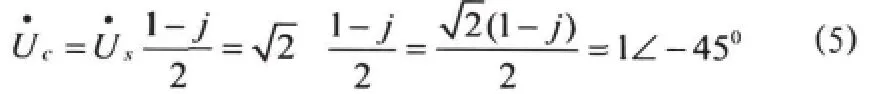
得相应的正弦稳态响应为

分析可知，稳态系统中，利用相量法只能求解得出系统正弦稳态响应，实际上就是零状态响应中的稳态响应，而无法得到零状态响应中的暂态响应，这正是学生在学习电路课程中容易忽略的知识点。

(2)利用频域分析法求解系统的零状态响应

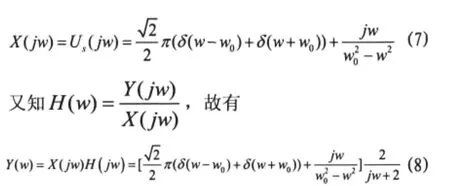
对上式直接求解傅里叶逆变换比较麻烦，由傅里叶变换性质，知

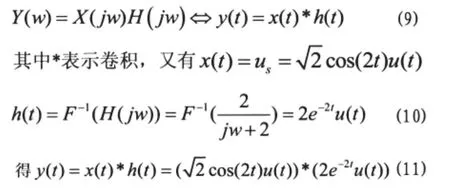
对式（11）查找卷积积分表可得

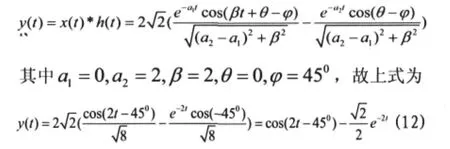
分析可知，利用频率响应法所得解第一项与用相量法所得稳态响应解是完全相同的，实际是零状态解的特解分量，第二项不能由相量法求得，为零状态响应中的暂态响应。这就表明两者在求解系统零状态响应时并不是完全一致的，这也正是学生在学习信号与系统课程中容易误解的地方。

(3)利用拉普拉斯变换法求解系统的零状态响应

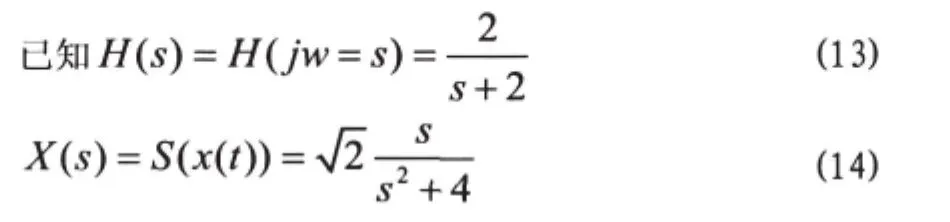
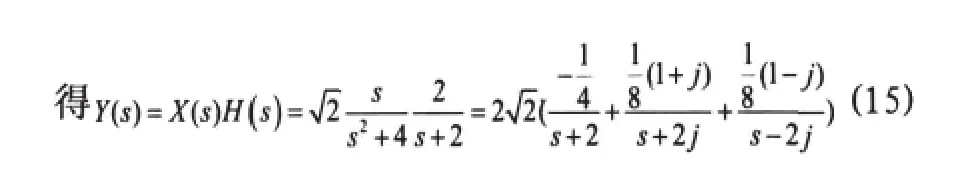
对上式求拉氏逆变换，查表可得：

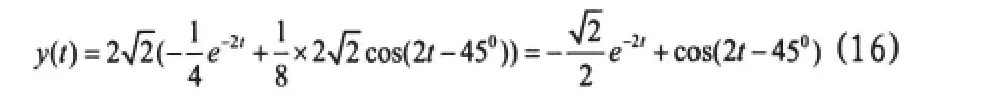
分析可知，前面所解结果与拉普拉斯变换法所得是一致的。

二、结束语

1.在求解系统的频率响应方面，相量法与傅里叶变换法是统一的，而且在已知具体网络系统时，可以直接使用电路的基本定理来进行计算，比傅里叶变换法更简便。

2.在分析系统的零状态响应方面两者是不等价的,相量法只是将正弦稳态的输出相量与输入相量联系起来,尤其需要重点指出的是该方法仅能确定系统零状态响应中的稳态响应分量,而无法求出暂态响应,且只适用于正弦激励情况。频域分析法是可以求解系统的整个零状态响应,且物理意义明显,但频域分析法存在一些不足,如傅里叶变换一般比较复杂且有时某些信号不存在傅里叶变换,无法利用频域分析法。

3.拉普拉斯变换法克服了频域分析法的不足，运算非常简洁，最具有普遍适用性。

[1]邱关源.电路(第五版)[M].北京：高等教育出版社，2006

[2]李瀚菘.电路分析基础（第四版）[M].北京：高等教育出版社，2006

[3]孟宪强，梁汝乐.改革“相量法”教学的尝试[J].电气电子教学学报，1990，4：42～45

[4]郭洪昌.相量法的产生与科学性讨论[J].长春师范学院学报（自然科学版），2007，3：38～40

[5]陈稀有，盛贤君，刘凤春.相量与正弦量的数学变换原理[J].电气电子教学学报，2007，2：36～39

[6]陈后金,胡健,薛健.信号与系统[M].北京：清华大学出版社,2003

[7]王宝祥.信号与系统[M].黑龙江：哈尔滨工业大学出版社，2000

[8]杨柏林，于德泳，钱培怡.建立在傅立叶变换理论上的相量法原理[J].抚顺石油学院学报， 2003，23（2）：72～73

[9]于德泳，马飞.浅析符号法（相量法）与傅里叶变换法的统一[J].电工教学，1997，1：31～33

The relationship and differences between phasor method and Fourier transform method

Dang Jianliang, Lin Aiying, Zhu Lianxuan, Wu Lili, Yuan Chao
Henan agricultural university, Zhengzhou, 450002, China

In this paper, the relationship and differences are mainly analyzed between phasor method and Fourier transform method in the"Circuit" and "Signals and Systems" courses. Phasor method, sine steady-state circuit analysis, frequency response and zero-state response analysis not only are focus and difficulties of their subjects respectively, but also play a key role in the follow-up courses. Based on the specific examples of teaching practice, the unity of phasor method and Fourier transform method in solving the frequency response is discussed, and the difference of them in analyzing zero-state response is researched in detail which many students misunderstood easily and not be explained concretely on many textbooks.

phasor method; Fourier transform; Zero-state response

2009-08-25

党建亮，硕士，讲师。

*本文系河南省教育厅自然科学研究指导计划(编号：2008B510010)。