手征媒质反射特性仿真计算*
2010-09-26童创明
吕 丹,童创明
(1.空军工程大学 导弹学院,陕西 三原 713800;2. 毫米波国家重点实验室,南京 210096)
1 引 言
双各向同性媒质的本构关系表达式中有介电常数、磁导率、非互易参数和手征参数4个参数,当非互易参数为零时,称这种媒质为手征媒质。
近几年,手征媒质在微带线、电磁透镜、极化转换器等方面展现出巨大的应用前景,同时反射特性的研究也是一个热点问题。文献[1-3]分别讨论了手征参数变化对反射系数的影响,另外,文献[2]还对不同本构关系下手征媒质的反射系数进行了仿真计算。随着研究的不断深入,将手征媒质涂敷在目标表面起到减小反射波进而降低目标的雷达散射截面(RCS)成为可能[4],文献[5]就计算了涂敷手征媒质金属锥柱的RCS。
文献研究成果只是基于固定的手征参数,并没有给出在相应的条件下应该将参数值设置成多少才能获得较好的吸收率。粒子群优化算法[6](PSO)需要计算的参数较少,原理简单、易于实现,但是它容易陷入局部最优值;而模拟退火算法[7](SA)能以概率接受差于目前状态的新状态,易于跳出局部最优。本文结合两种算法的优点,在标准算法的基础上给出改进措施,运用混合优化算法得到手征媒质的最佳参数,并在此基础上仿真计算了当一个参数取不同值而其它参数固定不变条件下电磁波垂直入射时的反射系数。结果表明,在给定的频率范围内、在最佳参数条件下,手征媒质的吸收率和反射系数都是理想的。
2 理论方法
2.1 手征媒质
2.1.1本构关系
在Lindell本构关系中,双各向同性媒质可描述为
(1)
(2)
式中,χ表示非互易参数,κ表示手征参数,ε0和μ0是真空中的介电常数和磁导率,ε和μ是媒质的介电常数和磁导率。双各向同性媒质包括手征媒质和非互易媒质,当χ=0时,称为手征媒质;当κ=0时,表征非互易媒质。
对于手征媒质,Lindell本构关系化简为
(3)
(4)
在Post本构关系中,手征媒质可描述为[1-2]
D=εpE+jξcH
(5)
B=-jξcμpE+μpH
(6)
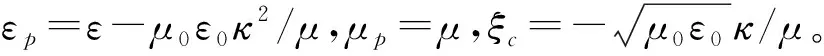
2.1.2反射系数
当平面波入射到双各向同性媒质表面时,场分成左旋极化波(-)和右旋极化波(+)。在Lindell本构关系下,波阻抗Z和波数β也相应的具有两种形式:
(7)
(8)
其中:
μ+=μ(cosϑ+κr)e-jϑ,μ-=μ(cosϑ-κr)ejϑ
(9)
ε+=ε(cosϑ+κr)ejϑ,ε-=ε(cosϑ-κr)e-jϑ
(10)
(11)

在空气与双各向同性媒质交界面上多层结构的反射系数为
(12)
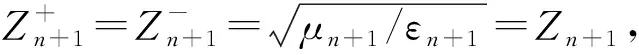
(13)
(14)
2.2 混合优化算法
2.2.1改进PSO算法
假设在一N维空间中,由M个粒子组成种群,第i个粒子的速度和位置分别为xi=(xi1,xi2,xi3,…,xiN)T和vi=(vi1,vi2,vi3,…,viN)T。粒子迄今找到过的最好位置称为个体极值点pi=(pi1,pi2,pi3,…,piN)T,种群目前找到的最好位置称为全局极值点g=(g1,g2,g3,…,gN)T。粒子位置与速度的更新公式为
(15)
(16)
式中,i=1,2,3,…,M;n=1,2,3,…,N;ω为惯性权重。
本文在标准PSO算法的基础上进行改进。
(1)混沌初始化
Logistic方程是一个典型的混沌系统[8]:
zn+1=μzn(1-zn),n=0,1,2,…
(17)
式中,μ为控制参量。
由任意初值z0∈[0,1]可迭代出一个确定的时间序列z1,z2,z3,…。粒子具有N维坐标,就要由一个N维任意初向量z0=(z01,z02,z03,…,z0N)T,z0n∈[0,1]迭代出一个数量L远大于种群的规模向量序列z1,z2,z3,…,zL,然后将混沌序列按下式一一映射到解空间:
xi=(xi1,xi2,xi3,…,xiN)T
xin=xnmin+(xnmax-xnmin)·zin
(18)
式中,xnmax和xnmin分别表示第n维坐标的上下限。
通过计算、比较适应值的大小,从中选择性能较好的M个粒子作为初始种群,同时随机产生粒子速度。
(2)重新初始化粒子的位置和速度
当迭代次数达到周期要求,对当前粒子的状态进行调整。这里采用选择机制,计算所有粒子当前的适应值,保留性能较好的一半粒子,另一半粒子再随机产生,所有粒子的个体极值点和全局极值点保持不变。
(3)变异
对种群最优点以外所有粒子的个体极值点按以下公式进行计算[9]:
(19)
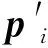
2.2.2改进SA算法
SA算法的原理是以固体的初始状态i作为当前状态,其能量为Ei;随机选取的某个粒子随机产生一个微小变化得到一个新状态j,其能量为Ej。若ΔE=Ej-Ei<0,则接受新状态;否则,以概率exp(-ΔE/kT)接受新状态。
本文在标准SA算法的基础上进行改进。
(1)初始温度
随机产生一组状态,选出两状态间的最大目标函数差值|Δfmax|。设初始接受概率为Pr,一般Pr在[0.7,0.9]之间,初始温度可由下式决定:
T0=-|Δfmax|/lnPr
(20)
(2)状态产生函数
由于混沌变量具有遍历性、随机性,文中采用产生混沌序列作为候选解的方式作为状态产生函数。
(3)温度管理
每一次外循环结束后都要下降温度,再进行下一次的内循化过程。这里采取较简单的线性下降策略:
Ti+1=Tiλ,0<λ<1
(21)
式中,λ越接近1,温度下降得越慢;λ越接近0,温度下降得越快。
(4)增加记忆功能
最优解记忆:将最优解设置设为初始状态,通过比较新状态与当前状态的目标函数值确定最优解是否需要更新,注意在以概率接受较差状态时最优解不变,这样保证了当前状态改变时历史最优解得以保留。
已接受解记忆:将已经接受过的状态存入禁忌表中,每次产生新状态后先对照禁忌表,如果曾经被接受过则重新产生新状态;否则按步骤4进行下面的判断。这样保证了同样的状态不会重复出现,节省了计算时间。
(5)内、外循环终止条件
文中采用了最优值连续若干步保持不变的原则。
2.2.3混合算法
在改进PSO、SA算法基础上,给出了改进的混合算法,具体流程如图1所示。
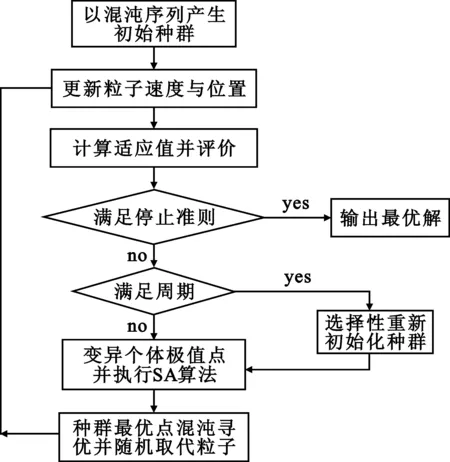
图1 混合算法流程图
2.2.4目标函数
优化设计的目的是要在给定频带范围内获得较大的吸收率和较小的反射系数,基底固定的手征媒质对反射系数有影响的变量是涂层厚度和手征参数。目标函数F为
(22)
对F进行最大值寻优计算将得到最佳的参数设置。
3 算例分析
(1)运用混合优化算法计算f(x)的最小值:
(23)
式中,xmax=1 000,vmax=1 000。
优化算法参数选取如下:c1=c2=2.0,惯性权重ω=0.375,粒子数M=30,最大迭代次数为10 000,初始化周期Ie=50,模拟退火内外循环的停止准则都是种群最优保持10次不变。图2是对函数进行50次计算平均最优值与迭代次数的关系[9],从图中明显看出本文改进措施使收敛速度大大提高。

图2 函数平均最优值与迭代次数的关系曲线图
(2)手征媒质的介电常数和磁导率分别是εp=4.73-j0.16,μp=1.07-j0.27,厚度d∈(0.000 1~0.01),手征参数ξc=ξc′-jξc″,ξc′∈(0.000 5~0.01),ξc″∈(0.000 01~0.006),入射波频率f∈(8,18)GHz。运用混合优化算法得到最优参数是:d=0.01,ξc=0.009 407 59-j0.004 880 79。改变手征参数实部,虚部及涂层厚度不变情况下,反射系数与频率的变化曲线如图3所示。
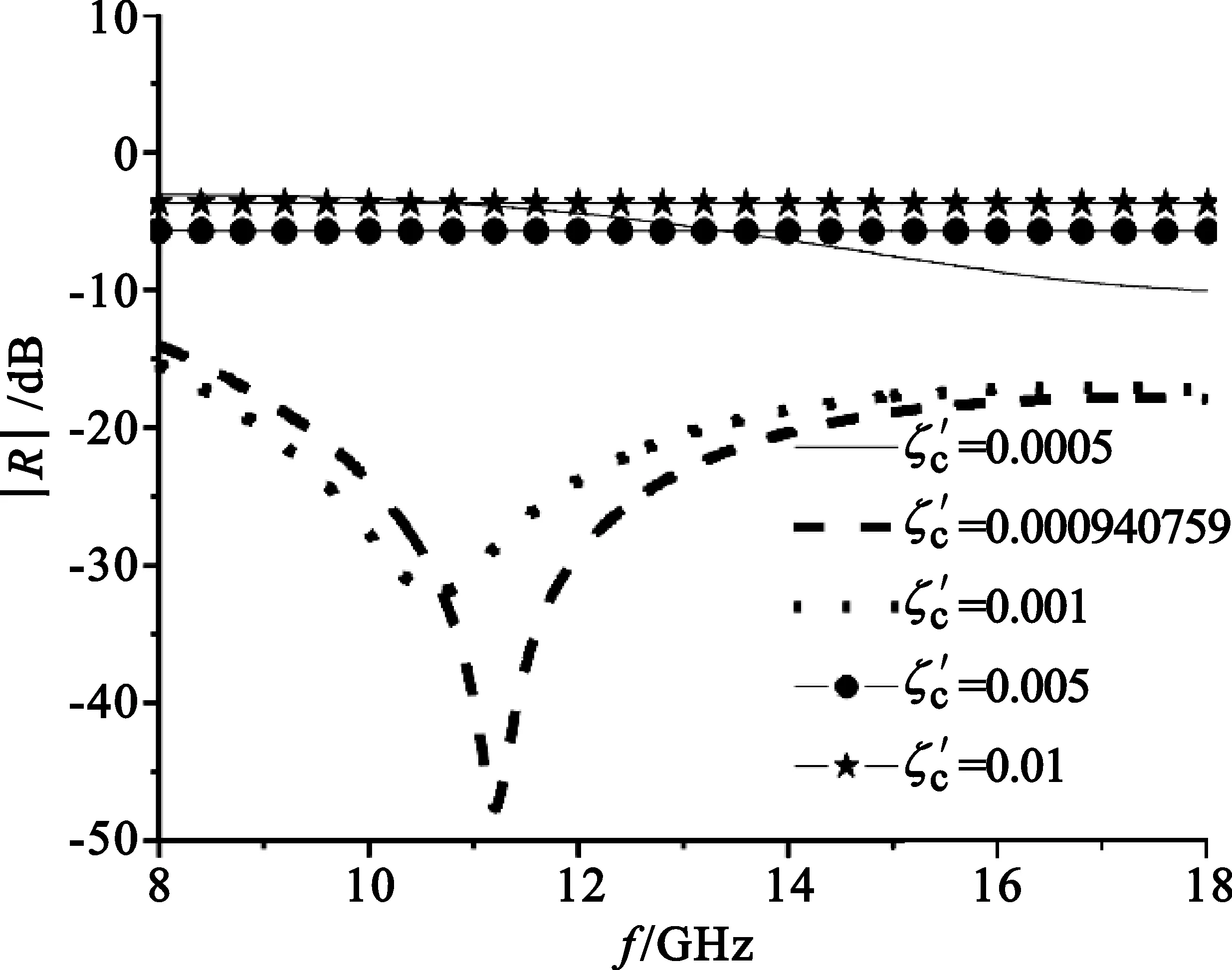
图3 ξc实部变化情况下的反射系数
由图3可以看出,随着手征参数实部的增大,反射系数整体上先下降再上升,而且吸收峰值点逐渐向低频端移动。当手征参数实部处于最优值附近时,在较宽的频带内都可以获得较理想的吸收率。
(3)改变手征参数虚部,实部及涂层厚度不变情况下反射系数与频率的变化曲线如图4所示。

图4 ξc虚部变化情况下的反射系数
由图4可以看出,随着手征参数虚部的增大,反射系数刚开始变化不明显,随后下降较快;虚部继续增大时反射系数又开始处于上升趋势。当手征参数虚部处于最优值附近时,吸波带宽都是较好的。
(4)改变手征涂层厚度,手征参数实部、虚部不变情况下反射系数与频率的变化曲线如图5所示。
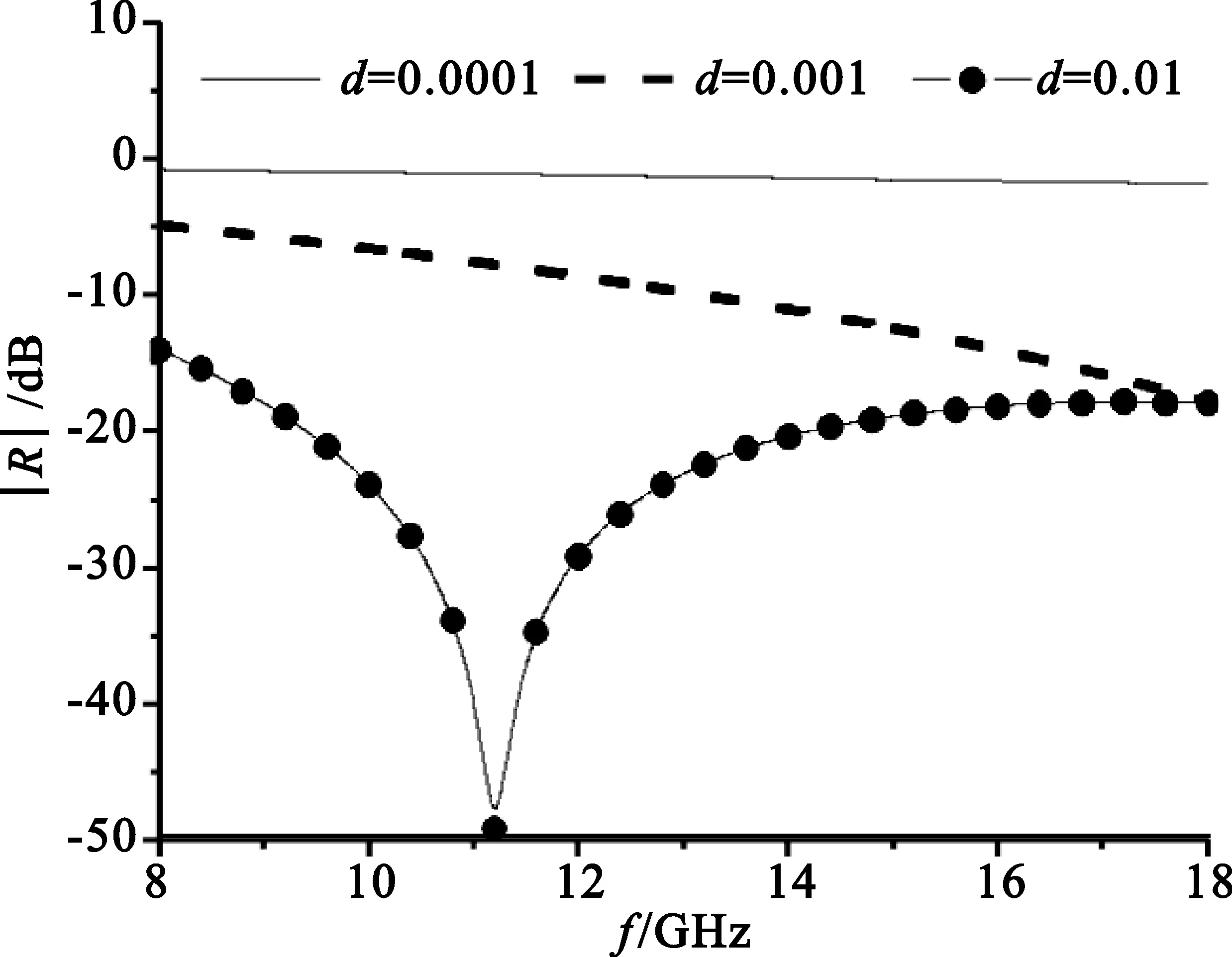
图5 涂层厚度变化情况下的反射系数
由图5可以看出,随着涂层厚度的增加,反射系数持续下降,而且吸收峰值点逐渐向低频端移动。当厚度取值在最优值附近时,可获得较为理想的吸波带宽。
4 结 论
手征媒质由于其手征参数的可调性使其不像一般材料那样拥有固定不变的介电常数,可以根据需要调整手征参数大小从而改变媒质介电常数值。通过优化算法的寻优计算,找到了最佳的参数设置,使在金属板上涂敷的手征媒质在电磁波垂直入射情况下,在一段频率上获得较小的反射系数和较高的吸收率,从而起到减小雷达反射波、降低目标RCS的作用。
参考文献:
[1] 刘述章,宋俐荣,符果行.手征媒质涂层参数对反射系数的影响[J].电子科技大学学报,1999,28(4):357-361.
LIU Shu-zhang, SONG Li-rong,FU Guo-xing. Effect of Chiral Medium Parameters on Reflection[J]. Journal of University of Science and Technology of China, 1999, 28(4): 357-361.(in Chinese)
[2] 肖中银. 电磁波在光子晶体和手征媒质中的传输特性[D]. 上海: 上海大学, 2004: 35-49.
XIAO Zhong-yin.The Propagation Property of Electromagnetic Waves in Photonic Crystals and Chiral Media[D].Shanghai:Shanghai University,2004:35-49.(in Chinese)
[3] 高成,舒永泽.手征媒质的手征参量ξc对反射特性的影响[J]. 南京航空航天大学学报,2000,32(5):522-526.
GAO Cheng,SHU Yong-ze. Influence of Chirality Admittanceξcon Reflection Characteristics[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2000, 32(5): 522-526. (in Chinese)
[4] 俞文明. 旋转对称频域和时域积分方程方法及其软件实现和应用[D]. 南京: 南京理工大学, 2007: 22-25.
YU Wen-ming. Frequency and Time Domain Integral Equation Methods for Bodies of Revolution, their Software Implementation and Applications[D]. Nanjing: Nanjing University of Science and Technology, 2007: 22-25. (in Chinese)
[5] 郭辉萍,刘学观,殷红成.手征材料涂敷导体目标电磁散射特性的PO分析[J].微波学报,2002,18(4):21-25.
GUO Hui-ping, LIU Xue-guan, YIN Hong-cheng. PO Analysis for Electromagnetic Scattering of Conducting Objects Coated with Chiral Material[J]. Journal of Microwaves, 2002, 18(4): 21-25. (in Chinese)
[6] EberhartR,Shi Y. Particle Swarm Optimization: Developments, Applications, and Resources[C]//Proceedings of the IEEE Congress on Evolutionary Computation. Seoul, Korea:IEEE,2001: 81-86.
[7] Kirkpatric S. Optimization by Simulated Annealing[J]. Science, 1983, 220(4598): 671-680.
[8] 高鹰, 谢胜利. 混沌粒子群优化算法[J]. 计算机科学, 2004, 31(8): 13-15.
GAO Ying,XIE Sheng-li. Chaos Particle Swarm Optimization Algorithm[J]. Computer Science, 2004, 31(8): 13-15. (in Chinese)
[9] 杨光友. 混合粒子群优化及其在嵌入式智能控制中的应用[D]. 武汉: 武汉理工大学, 2006: 22-66.
YANG Guang-you.Hybrid Particle Swarm Optimization and Its Application in Embedded Intelligent Control[D].Wuhan:Wuhan University of Technology,2006:22-66.(in Chinese)
