同波束干涉测量技术测量精度仿真研究*
2010-09-26
(中国西南电子技术研究所,成都 610036)
1 引 言
航天测控中,通常采用多个地面站对同一飞行器的测轨数据进行拟合的方法得到较高的测量精度,参与运算的数据量大,数据处理时间长,精度有限,且无法解决同一波束内多个目标相对位置的测量问题。同波束干涉测量(Same Beam Interferometry,SBI)技术利用两个地面站同时接收两个空间目标下行信号进行差分处理,大气、等离子体等介质差引入的传输时延误差和接收设备的时延等误差项几乎被抵消,可实时解算得到两个航天器的高精度相对位置数据(可达米级),这种方法是目前公认的优秀的高精度测量技术[1]。
SBI测量技术使用载波相位而不是群时延(或延迟率),可以达到的测量精度比传统的航天器类星体干涉仪要提高3倍以上。SBI比传统航天器干涉具有一些操作上的优越性:由于不需要用射电星进行系统校准,在数据处理过程中也不需要互相关步骤,可实现飞行器的实时相位测量。相位测量数据的处理更像传统多普勒数据。同波束干涉数据与双向多普勒或单/双向多普勒相结合,有可能成为强有力的轨道确定数据类型,并可以同时跟踪多个航天器[2]。
1990年8月~1991年4月,NASA在对金星轨道飞行器Magellan与Pioneer12进行测量时就采用了SBI技术,采用S频段测出的两个飞行器在天平面上的位置变化量小于10 m,X频段小于4 m。1993年,NASA在实施“火星观测者”计划过程中,同时采用多普勒数据和SBI数据使火星着陆器——漫游车的相对位置定位精度优于5 m[3,4]。
在我国的星群卫星、共位卫星测控和载人空间站交会对接等多目标、高精度测控任务中,采用SBI技术可大大提高目标的相对位置测量精度。
2 SBI测量技术基本原理
同波束干涉测量是指当两个航天器角度非常接近时,处于地面天线的同一个波束之内,可以在地面天线同一波束内进行测量。使用两个地面天线对两个航天器同时观测,可以进行差分干涉测量。考虑两个航天器同时向两副地面天线发射无线电信号的情况,地面每副天线可以同时捕获2个航天器的下行信号。同时测量两个航天器发出的信号载波相位,经过实时双差分处理,可以得到两个航天器之间的相对距离及其变化信息。
SBI测量原理示意图见图1。SBI提供了从地球看航天器之间的角度间隔测量值,观测值由测量飞行器射频载波信号的相位得到,首先是两个观测站产生差异,然后是飞行器之间产生差异。视距相位测量误差可通过二次微分来减小。
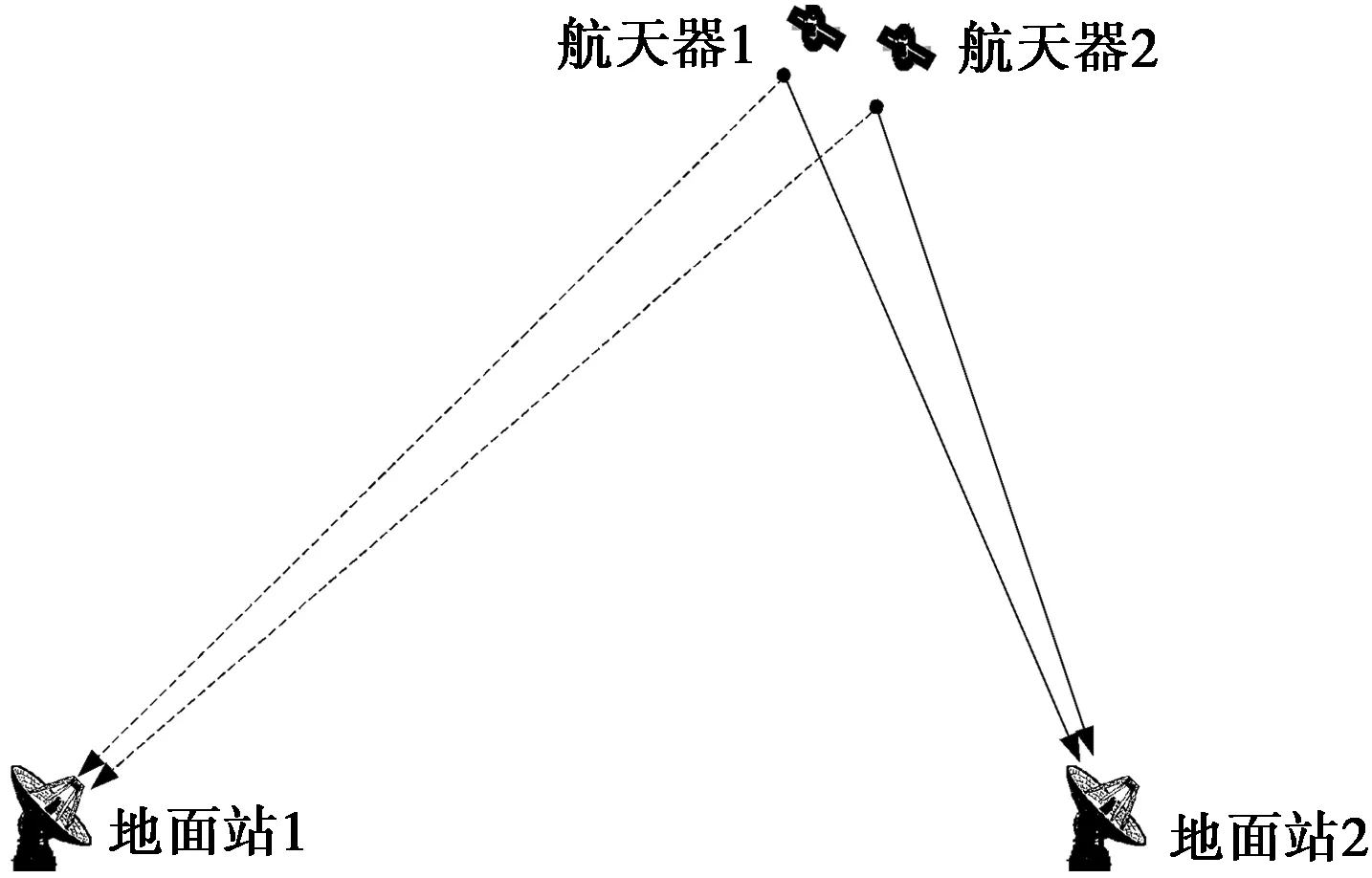
图1 SBI测量原理示意图Fig.1 Sketch map of SBI measuring principle
由于目标相对于地面站的空间距离不同,两个航天器的发射信号不可能同时到达两副地面天线中的任一副天线,因此地面站接收到的两个下行信号的时延也不相同。地面接收信号的时延取决于连接两个地面天线的矢量与从地面到航天器的矢量之间的角度。但是,各种误差源恶化了该时延的测量,包括系统测量仪器引起的时延、信号通过中性介质和带电介质引起的时延等。
将同时从两个航天器获得的观测值进行差分,可大大消除这些误差的影响,得到的双差分时延提供了极精确的航天器间角度间隔的测量值,其方向与地球基线在天空面上的投影平行。累加两副地面天线接收到的航天器信号相位,可得到由两个航天器和两副地面天线获得的SBI观测值。
如果每个航天器发射的信号频率为f,则双差分时延τ可以表示为
(1)
式中,φij(t)表示航天器i发射、地面站j接收的信号相位,b为载波相位偏差整数。
由于有未知整数偏差,SBI测量值不直接提供双差分时延。但是在一段时间内连续获得的SBI测量值共享相同的偏差,在双差分时延内对时间变化量提供精确测量值。
给出有关航天器状态的足够的先验信息,就可以解整周模糊,确定绝对双差分时延。通常,有关航天器状态的先验信息不足以确定整周模糊,因此必须估算SBI的相位偏差。如果SBI相位偏差估算值的∑值小于载波相位周期的1/6,解整周模糊的确信度为99%。可以通过一系列间隔越来越宽的侧音对自行解出相位模糊,从而得到载波的SBI相位偏差。整周解模糊问题本文不作讨论。
3 测量误差及数学模型
影响SBI测量精度的主要元素包括太阳等离子体、大气环境、系统噪声、天/地频标不稳定度、地面设备误差、时钟不稳定性、未校准的介质延迟,以及跟踪站位置误差等[5~7]。
SBI系统主要测量误差项的分析如下:
(1)系统噪声
接收信号包含航天器的信号和地面接收机产生的噪声,它与系统工作温度成正比。系统噪声误差取决于接收信号功率与噪声功率之比。将电压信噪比(SNRv)在较长的时间段内平均,可以变得更高。系统噪声引起的SBI相位误差为
(2)
式中,λ为接收信号波长。
(2)非线性相位偏移
将两个航天器发射的正弦信号和两个地面站接收的正弦信号相位测量值进行双差分,得到SBI观测值。相移被引入地面接收机链路,它取决于多普勒频移信号的频率,因此每个站和每个航天器的相移通常是不同的。设备相移可以分为随频率线性变化的相移(不分散的)和与频率有非线性关系的相移(分散的)两类。分散误差约为
εd(mm)=2×(0.5° )×λ/(360°)
(3)
式中,0.5°是现用VLBI接收机系统中典型的设备相位偏移。每个航天器在每个地面站有个别误差,因此采用系数2。使用更好的设备或非常接近的航天器频率可以减小相位偏移的影响。
(3)振荡器漂移
两个航天器发射机频率的未知偏差会引起一个误差,表示为
εd(mm)=cτ×Δf/f
(4)
式中,c为光速,τ为2个站的接收时间差,f为航天器发射频率,Δf为发射机频率的未知偏差。对于双向传输,两个航天器与地面站分别建立上行链路,由地面站时频分系统提供Δf/f估值,为5×10-14。对于单向传输,用视距多普勒测量值估算航天器振荡器额定频率的修正值。振荡器频率的估算精度取决于跟踪覆盖面和振荡器稳定性,Δf/f在单向传输时的估算精度为2×10-12。
(4)基线测量误差
由于角度测量是由2个地面站的接收时间得出的,地面站位置和地球方位的不确定性降低了对SBI测量值的判读。地球两极的方位和旋转速度是随机变化的,必须进行监视以保持对这些量的了解。目前可以达到的地面站基线测量精度为5 cm以下。用7 cm的数值来表示由地面站位置和地球方位不确定性引起的基线误差比较适中。SBI误差为
εd(mm)=70mm×Δθ
(5)
(5)地面站设备误差
地面站设备未校准的群时延或时钟偏差会引起下列形式的相位延迟误差
(6)
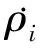
(6)太阳等离子体
4条信号路径穿越行星际空间时,间隔几百或几千公里,不会完全消除太阳风中带电粒子引起的延迟误差。太阳等离子体延迟误差与信号频率的平方成反比,随太阳-地球-航天器(SEP)角度的减小而增加。采用薄屏冻结湍流模型来模拟等离子体引入的误差。
NASA的相关资料已显示了模拟试验结果。对航天器间隔角较小的情况,差分延迟误差与间隔角和SEP角几乎是线性关系。这个模型在SBI测量中的适用性还需要通过一些试验数据来检验。
(7)电离层
用GPS测量值提供电离层校准数据。在X频段,地球电离层延迟映射到经过校准的视线上的误差约为30 mm。两条靠近的视线的差分延迟误差εd为
(7)
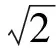
映射函数代表电离层校准中最大的不确定性,对于SBI数据所需的间隔角较小时的情况还不太了解。如果间隔角在仰角上,用于GPS校准的映射函数的导数最大值为3.5/rad,这里取5/rad更保守一些。
(8)对流层
对流层误差表示为
(8)
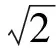
(9)SBI总误差
总的星间距离误差为上面各项均方和:
(9)
4 仿真方案
根据地面站1、地面站2的位置,仿真得到某一时刻同时对两个目标的仰角、空间时延。选用STK仿真软件作为仿真引擎,仿真得到的数据存入仿真数据库,并通过Matlab的接口,借用Matlab强大的数值分析计算及图形显示功能对数据进行分析。仿真研究主要包括SBI测量误差模型的构建、STK软件系统参数的优化选择、Matlab数据处理方法研究等内容。
仿真结构图如图2所示。仿真过程为:首先启动主控模块,并完成STK的初始化,然后由用户通过主控模块建立STK实体模型,并控制实体模型的运行;获取由STK实体模型返回的各种数据,完成数据实时显示和将数据存入仿真数据库的操作;最后调用由Matlab生成的动态库程序,借用Matlab强大的数值处理和绘图功能,将数据库中的数据进行处理、显示。
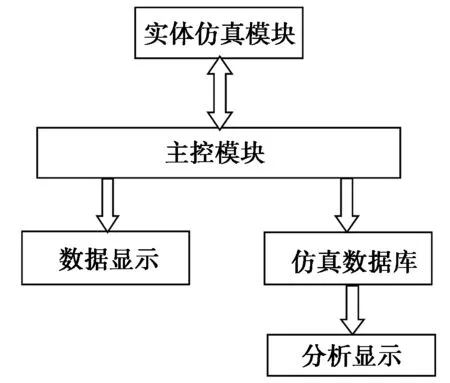
图2 系统仿真结构图Fig.2 System simulation structure
4.1 卫星轨道参数及星下点计算模型
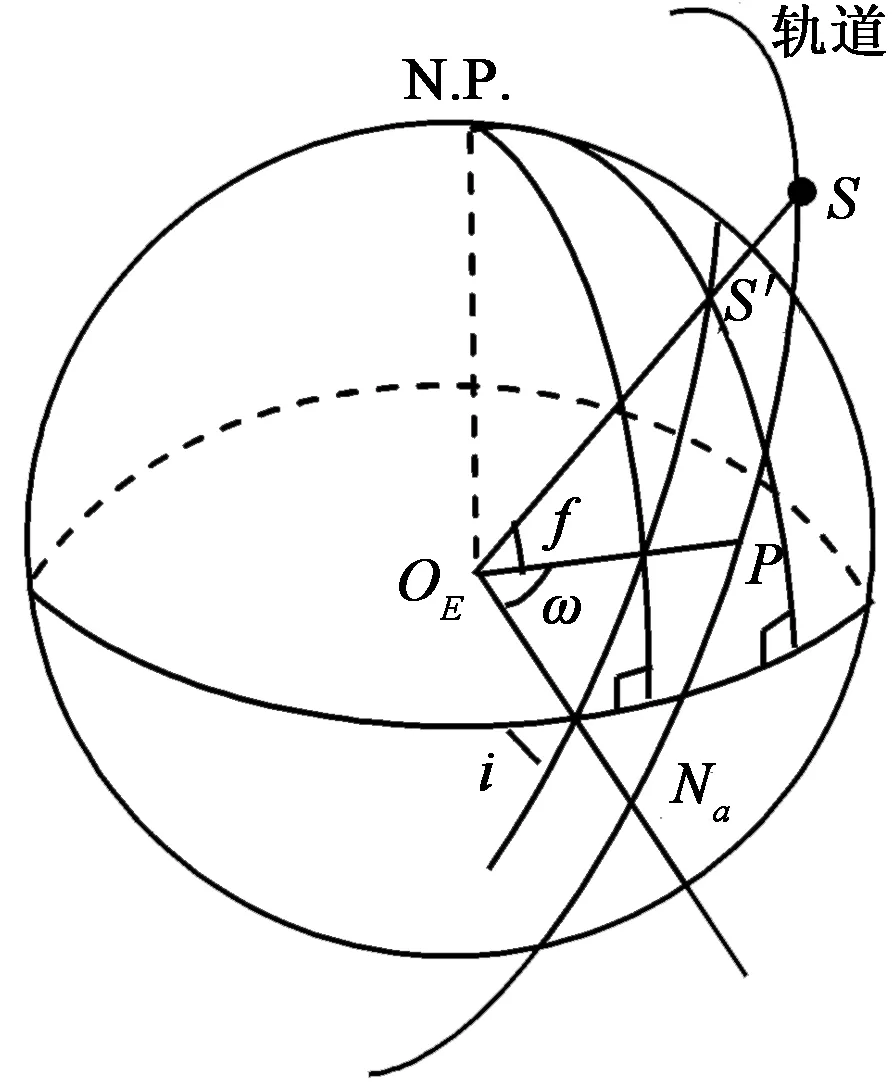
图3 卫星星下点轨迹及有关参数Fig.3 Footprint of satellite and some parameters
4.2 分析数据生成与预处理模型
在时间T(min)内,可计算确定每颗卫星过站的时刻和持续时间,每颗卫星过站时间分析数据生成一个与时间t对应的向量Dm,即:
Dm={am(t),t=1,2,…,T,T},m=1,2,…,M
(10)
式中,am(t)=1或0,为1时表示卫星处于地面站观测范围内,0则相反。显然,向量Dm是最原始的分析数据,如果考虑地面支持计划安排,可能对短时间(如2 min以下)过站卫星不进行地面服务,为此则需要对分析数据进行滤波。滤波算法可采用模板匹配法,如对2 min以下数据进行滤波,则模板为[0 1 1 0]和[0 1 0],采用这两个模板在向量Dm中进行滑动,所有与之匹配的向量元素均置为0,从而可滤除2 min及以下过站时间分析数据。
经过预处理生成的数据已经不是单纯的过站时间数据,但从分析意义上讲,仍然可以将天线系统一次调整时间(滤波后的卫星实际过站时间+准备时间+后处理时间)当成一次过站时间,这样形成新的分析数据表示成向量形式为
(11)
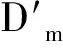
Tm=(tmi;Lmi),m=1,2,…,M
将向量Tm(m=1,2,…,M)复合,并按各次过站时刻起点tm按升序排序,相应的过站时间长度Lm保持与tm的位置关系不变,假设这样排列的二维向量具有如下的形式:
(12)
可以看出:
当ty1-tx1>Lx1时,第x颗和第y颗星不是同时过站,反之为一次同时过站;
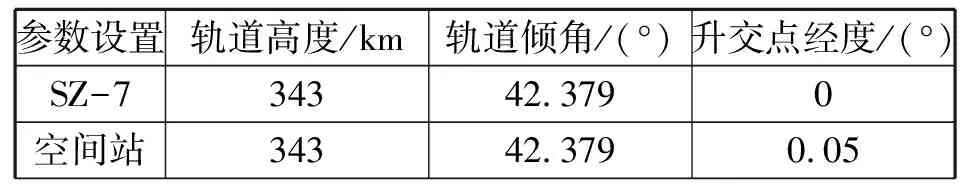
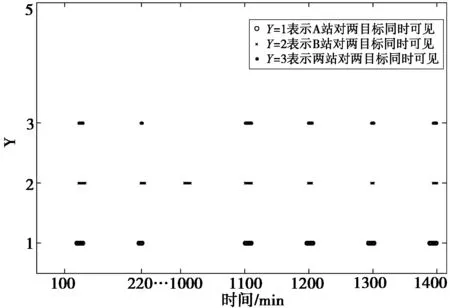
当ty1-tx1 当ty1-tx1 利用STK来解决参数获取问题,输入的参数可从STK得到的仿真数据库中读取。需要确定的参数有工作频段(S、C、X、Ka)、地面天线仰角E、两个站对两目标下行信号的接收时间差τ、两个站对两目标观测时间t、单目标对单站过站时间T。 STK/Chains模块可以距离目标网络来进行对象间的可见性分析,STK的Connect模块可以使用户方便地与STK实现系统集成。 数据处理主要用Matlab来实现。Matlab编程语言具有强大的数值计算和计算结果可视化功能,并拥有强大而开放的工具箱,借用Matlab强大的数值计算和绘图功能,对姿态数据进行处理显示,具有直观、简便的优点,并可缩短程序开发周期。 根据输入的参数进行计算后,输出的结果主要包括系统噪声引入的误差、非线性相位偏移引入的误差、振荡器漂移引入的误差、基线测量引入的误差、地面站设备引入的误差、电离层引入的误差、对流层引入的误差、总的距离误差。 5.1.1 仿真参数设置 两个地面站的参数:A站和B站的经度、纬度。 两颗静止卫星参数:GEO1仰角E=160°;GEO2仰角E=160.007°。 仿真时间24 h,采样间隔为1 min。 5.1.2 仿真结果 仿真结果见图4和图5,仿真数据参见表1。 图4 24 h地面站对两颗卫星的仰角Fig.4 Elevation of two satellites during 24 hours 图5 两站对两颗卫星接收时延差Fig.5 Receiving time delay of two satellites for each station 参 数频 率(SNR=43 dBHz)/MHz2 2003 7007 25017 000系统噪声误差/m3.069 261.824 970.931 3620.397 198非线性相位偏移/m0.000 378 7880.000 225 2250.000 114 9434.90196E-5振荡器漂移/m2.13029E-62.13029E-62.13029E-62.13029E-6基线测量误差/m6.10865E-66.10865E-66.10865E-66.10865E-6地面站设备误差/m2.54E-102.54E-102.54E-102.54E-10电离层误差/m0.000 018 5120.000 018 5120.000 018 5120.000 018 512对流层误差/m2.80931E-52.80931E-52.80931E-52.80931E-5总误差/m3.069 261.824 970.931 3620.397 198 5.2.1仿真参数设置 “神舟”七号飞船(SZ-7)轨道参数、空间站轨道参数见表2。 表2 轨道参数Table 2 Orbit parameters of SZ-7 为保证飞船和空间站能在地面站的一个波束以内,空间站与飞船之间的平均距离保持在6 km左右(4~7 km);其它参数同前。 5.2.2仿真结果 5.2.2.1地面站对目标的可见情况 (1)在24 h内的可见情况 A站对两目标同时可见的时间有6段;B站对两目标同时可见的时间有7段;两站对两目标同时可见的时间段有6段,如图6所示。 图6 24 h两地面站对两目标同时可见时间段Fig.6 The available time slot of two objects for each station during 24 hours (2)目标仰角情况 在最长可见时间段1 101~1 110 min,各站对目标的仰角情况如图7所示。 图7 各站对各目标的仰角Fig.7 Elevation of two objects for each station 在最长可见时间段1 101~1 110 min,各站对目标的接收时延差如图8所示。 图8 两站分别对两目标的接收时延差Fig.8 Receiving time delay of two objects for each station 当两个地面站均为低仰角时测量误差最大。取t=18∶23∶46,两站仰角均较低。测量参数设置见表3,各频段测量误差见表4。 表3 测量参数设置Table 3 Measuring parameters 表4 各频段测量误差Table 4 Measuring error for each frequency SBI技术是解决相对位置高精度测量问题的先进方案,本项目利用STK仿真平台和Matlab软件完成了GEO卫星之间、飞船与空间站之间的SBI测量仿真工作。通过相关的试验结果可以看出: (1)利用我国现有的陆基测控网做支持,采用SBI测量技术进行同步共位卫星、小卫星星群相对距离测量,S频段可达到3 m的精度,C频段精度小于2 m,X频段(待建)小于1 m,Ka频段(待建)小于0.5 m; (2)在宇宙飞船与载人空间站交会对接测控支持方面,无论采用S频段还是Ka频段,SBI测量精度均优于0.5 m。 由此可见,除了深空探测应用以外,SBI技术还可广泛应用到小卫星组网、共位卫星管理和空间交汇对接等多个军民用测控领域,具有广阔的应用前景。 参考文献: [1] Kahn R D,Folkner W M,Edwards C D,et al.Position Determination of a Lander and Rover at Mars with Earth-Based Differential Tracking[R]//TDA Progress Report.[S.l.]:[s.n.],1991:42-108. [2] Conselman C C,Hinteregger H F,Shapiro I I.Astronomical Applications of Differential Interferometry[J].Science,1972,178(4061):607-608. [3] Folkner W M,Border J S.Orbiter-Orbiter and Orbiter-Lander Tracking Using Same-Beam Interferometry[R]//TDA progress Report.[S.l.]:[s.n.],1992:42-74. [4] Border J S,Folkner W M,Kahn R D,et al.Precise Tracking of the Magellan and Pioneer Venus Orbiters by Same-Beam Interferometry Part I:Data Accuracy Analysis[R]//TDA progress Report.[S.l.]:[s.n.],1992:86-110. [5] FolknerW M,Border J S,Kahn R D,et al.Precise Tracking of the Magellan and Pioneer Venus Orbiters by Same-Beam Interferometry Part II:Orbit Determination Analysis[R]//TDA progress Report.[S.l.]:[s.n.],1993:42-113. [6] Edwards C D,Goldstone Intracomplex Connected Element Interferometry[R]//TDA progress Report.[S.l.]:[s.n.],1990:42-101. [7] Folkner W M,Border J S.Orbiter-Orbiter and Orbiter-Lander Tracking Using Same-Beam Interferometry [R]//TDA progress Report.[S.l.]:[s.n.],1992:42-109.4.3 仿真参数获取
4.4 数据处理
4.5 输出结果
5 系统仿真结果
5.1 被测目标为两颗共位卫星

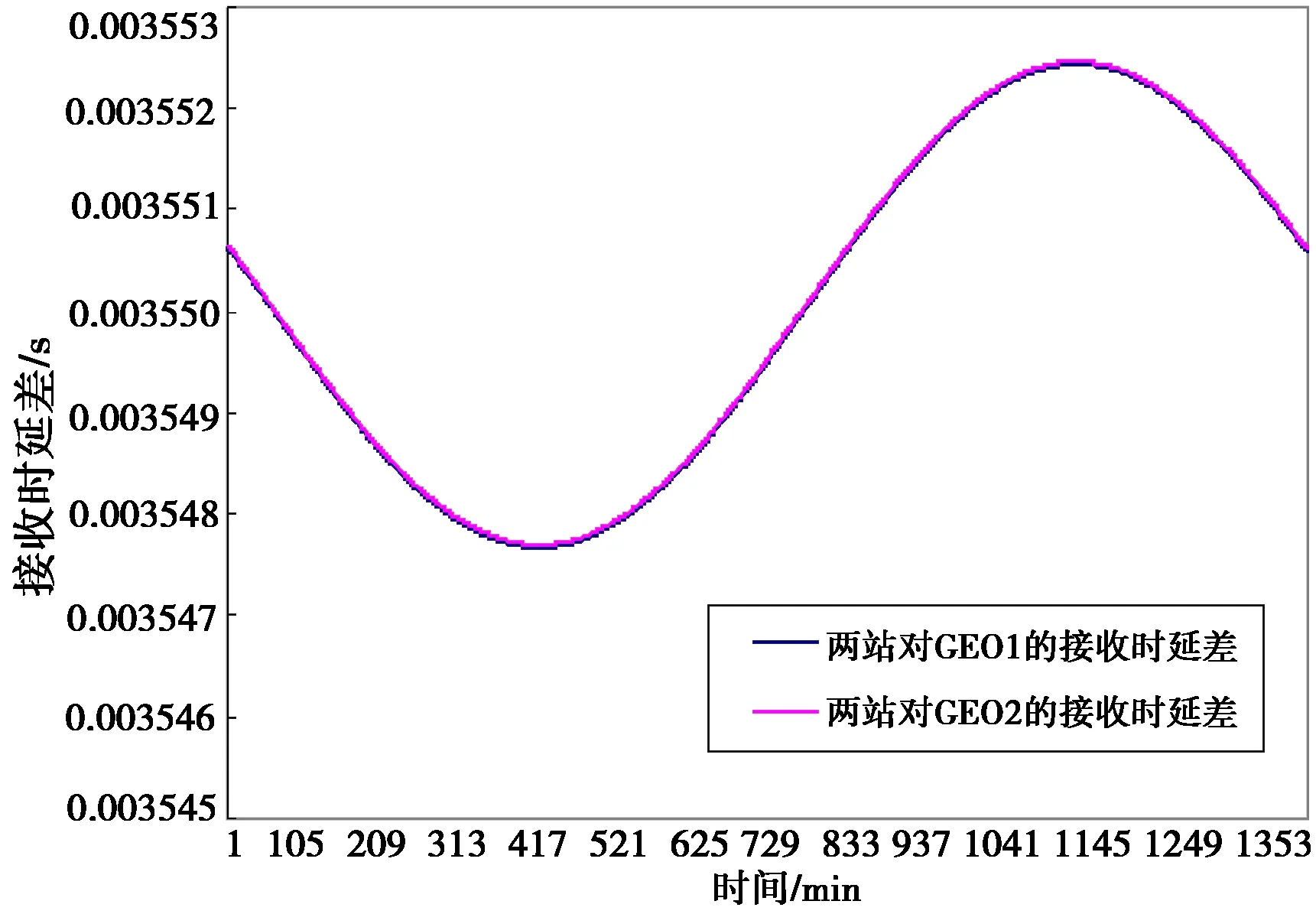
5.2 被测目标为飞船和空间站
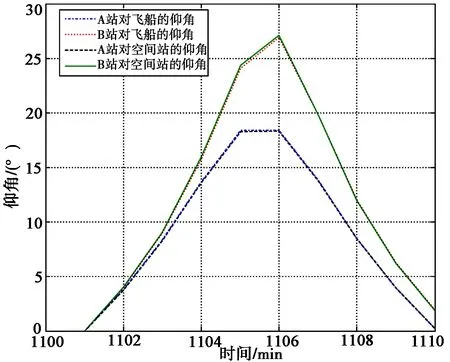
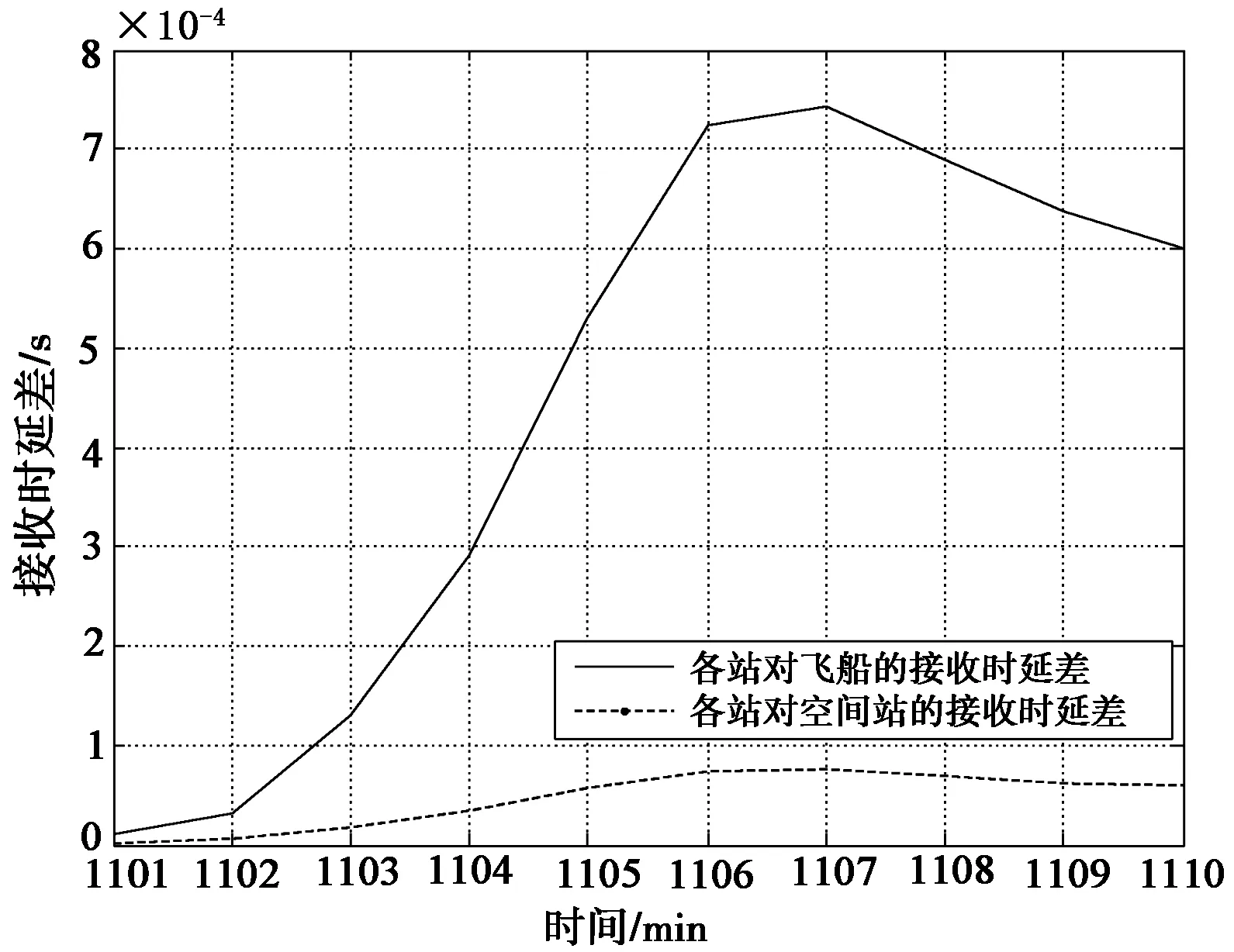
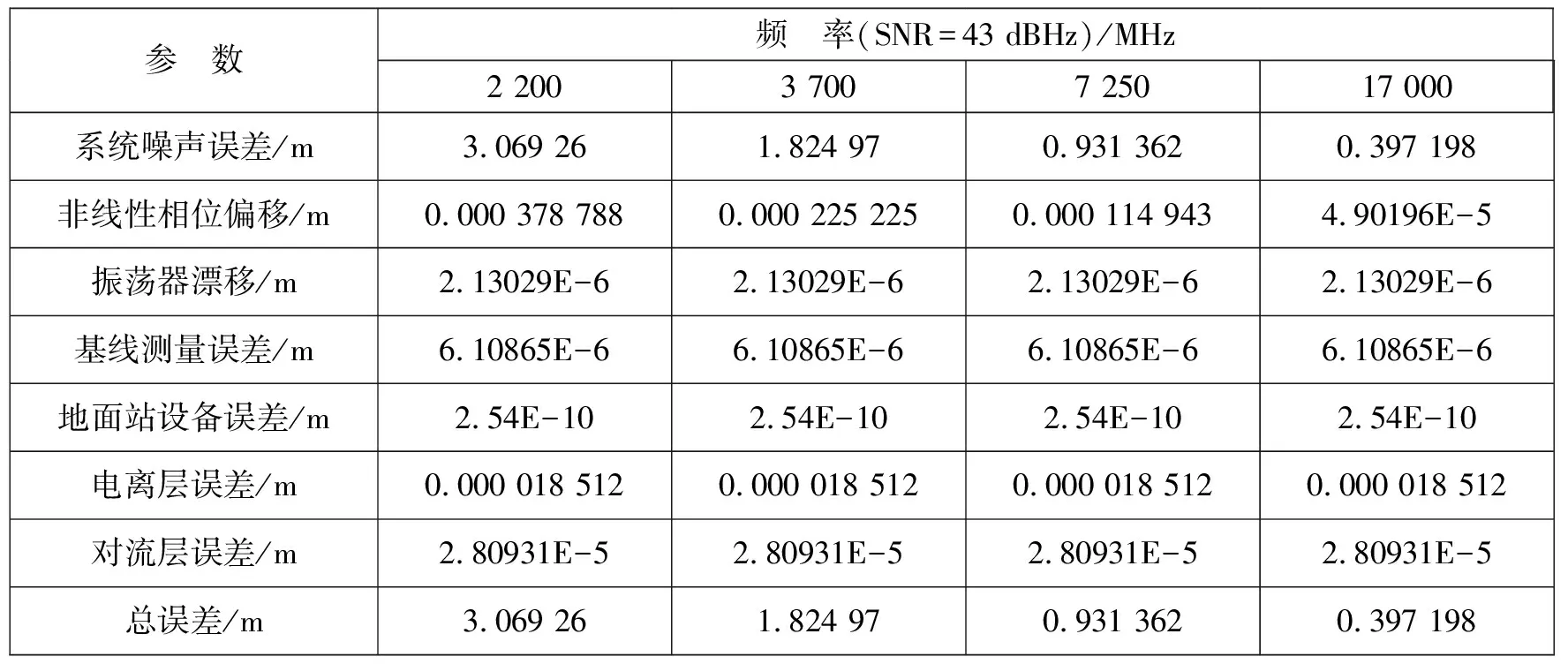
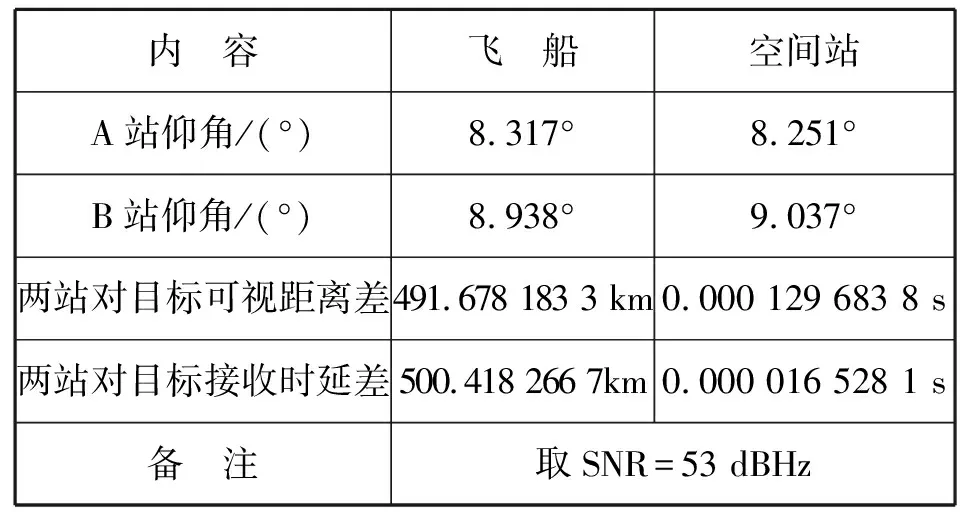
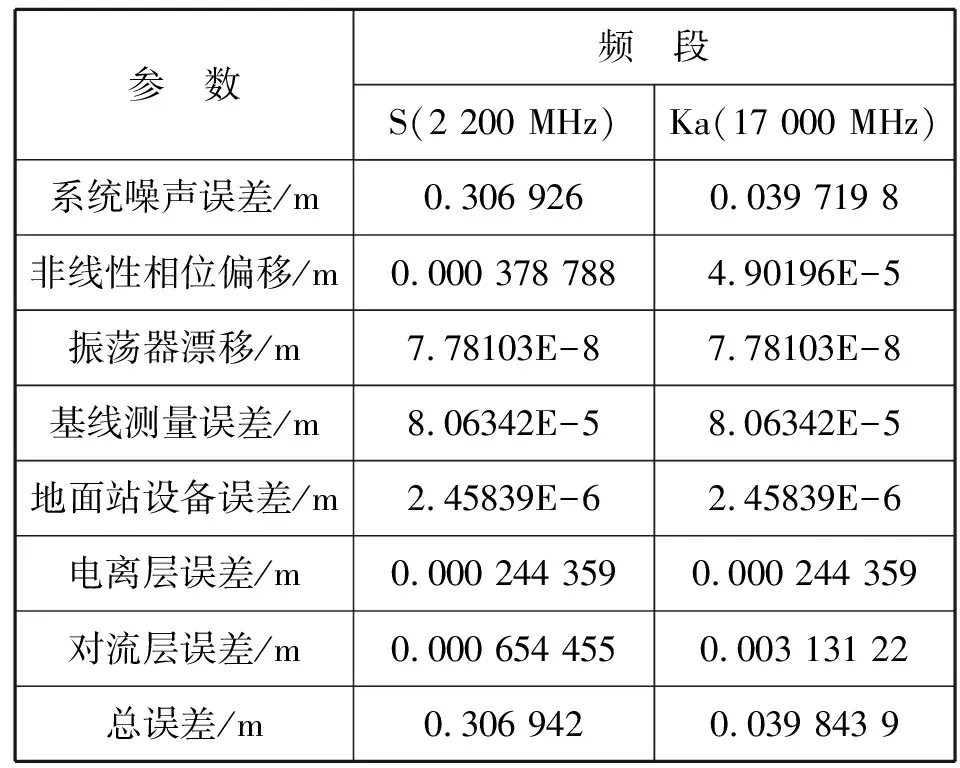
5.2.2.2 测量误差计算
6 结 论
