直齿圆柱齿轮冷挤压成形腔参数优化

孟冠军， 赵 韩， 陈 科

（合肥工业大学机械与汽车工程学院，安徽 合肥 230009）

直齿圆柱齿轮冷挤压成形腔参数优化

孟冠军， 赵 韩， 陈 科

（合肥工业大学机械与汽车工程学院，安徽 合肥 230009）

针对齿轮冷挤压技术存在的成形压力大和坯料填充困难问题，建立了流线型的直齿圆柱齿轮冷挤压成型腔几何模型，并对挤压过程进行了数值模拟。结果表明，流线型挤压腔能够在较小的成型力下保证挤压齿轮齿形填充饱满。通过对模拟过程的分析，研究了不同坯料放大半径λ值对成型腔形状和挤压方式的影响，并通过对不同成型腔的数值模拟，得到最优的参数模型。

机械制造；参数优化；数值模拟；直齿圆柱齿轮

齿轮作为传递运动和动力的最基本零件之一，在工程领域有着非常广泛的应用。直齿圆柱齿轮冷挤压成形不需要加热坯料，成形零件具有表面质量高、尺寸精度高的特点，具有很大的市场应用前景，但成形时材料的温度低，变形抗力高，流动性差，致使锻造载荷陡增，齿形充满困难，模具变形磨损严重，寿命低。齿轮冷精锻成形目前的主要问题是如何在保证齿腔角隙充满的条件下降低工作压力。

本文针对齿轮冷锻过程中存在的两个关键问题——保证齿形充满和降低成形压力，提出设计符合金属流动轨迹规律的挤压腔的设计思想，和基于分流原理的直齿轮镦挤复合的工艺思想，将流体力学中的流曲线的概念和等截面积变化的理论引入到型腔设计中来，建立流线型的挤压成形腔，数值模拟结果表明，成形腔对于增强金属的流动性，降低齿轮成形载荷等，具有积极作用。

1 挤压型腔建模

直齿圆柱齿轮挤压腔设计的重点是齿根的流线型变化及齿形的等面积比变化，依据的理论是流曲线曲面理论与等面积比变化理论。建模的过程是一个从复杂曲线系统到曲面体统，再到实体模型的过程。整个建模的思想是从原始型值点拟合样条曲线，然后从样条曲线拟合曲面，再整合各部分曲面，然后再通过镜像和阵列得到完整的齿形曲面，最后再通过布尔运算得到挤压腔模型[1]。基于流曲线理论和等面积变化理论建立的齿轮挤压腔模型如图1所示。

图1 挤压腔模型

2 挤压腔数值模拟及结果分析

在建立挤压腔几何模型后，采用DEFORM软件对挤压过程进行了数值模拟[2-3]。直齿轮冷挤压是在630t冷锻压力机上完成的，为了真实模拟直齿轮冷锻成形过程，采用位移载荷来模拟压力机的静压力，忽略锻件在成形过程中的温度变化。取实体模型的1/2，采用四节点实体单元进行网格划分。以凸模端面和凹模型腔面为目标面，坯料表面为接触面，采用接触单元模拟坯料与凸凹模之间的摩擦，摩擦系数取0.12，工件的材料选用20#钢。

凹模挤压腔基本参数设定如下：

齿数z=22；模数m=2.5；轮齿厚度L=10mm顶隙系数c*=0.25；分度圆压力角20α=°；坯料放大半径06.1=λ

材料的基本参数设定：

弹性：杨氏模数 206754； 泊松比 0.3；热膨胀系数 1.2e-005；热辐射系数 0.7

应变反映的是工件的一个区域在外力作用下的总累计变形。DEFORM用不同的颜色代表不同的变形程度，图2是齿轮在不同时刻（第40和60增量步）的应变情况。从图中可以清晰地看出，整个挤压过程挤压凹模变形区的型腔各区域都能顺利完成金属填充，整个齿形饱满平滑；齿顶圆角已经充满，没有塌角缺陷；齿根圆角过渡圆滑，没有折叠缺陷。

在齿轮成形过程中，工件的等效塑性应变分布变化较大。从图中可以看出, 累计变形最大的，大约都分布在齿部及齿根附近的区域；齿轮中心区域，累计变形量相对较小。变形大的区域在齿顶处变形最为显著，齿根变形较小，这在一定程度上符合了本文齿轮挤压腔造型的初衷，齿根的流线形过渡使这部分金属应变相对较小。

图3是齿轮在不同时刻（第40和60增量步）各区域所受变形力的情况。与应变场的模拟结果相似，变形大的区域受的变形力也较大。齿轮坯料受力最大的区域都分布在齿形相近区域，且以齿定处受力最为显著，齿根受力相对略小，符合本设计方案的初衷。从变形力的大小来看，变形显著的齿形处的变形力基本都在600MPa以下，小于目前模具材料2500～3000MPa的强度极限。

图2 齿轮冷精锻过程坯料应变分布

图3 齿轮冷精锻过程坯料应力分布

3 挤压腔主要参数优化

3.1 优化参数选择

模拟结果表明，齿轮角隙充填性能良好，因此本文在保证造型方案不变的基础上，针对一个重要的参数，坯料放大半径λ来进行优化。通过选定不同的λ值，得到了不同形状、不同挤压方式的挤压腔，让它们在相同的参数设定下进行数值模拟，然后对结果进行综合比较，来得到最优的造型参数值。

当坯料放大系数取不同参数时，挤压腔形状变化很大。坯料放大系数λ值为1时，齿轮截面积和坯料截面积相同，此时的冷挤压方式为复合挤压；而当坯料放大系数值λ为1.11时，坯料半径已经接近了齿轮的齿顶圆半径，当坯料放大系数λ超过这个值，挤压方式就变成了完全的正挤压，因此λ值为1.12时是挤压方式从复合挤压变到正挤压的分界点。在选择参数值时，除了1.06外，又分别为λ取了1.00、1.10、1.20，得到如图4所示形状变化较大的挤压腔模型。当λ取1.0时，坯料直径小于齿轮分度圆直径，意味着冷锻过程中金属从齿根流向齿顶的深度要比其它型腔深一些。当λ取1.1时，坯料半径略小于齿顶圆半径，接近正挤，当取1.2时，坯料半径大于齿顶圆半径，挤压方式为完全的正挤，冷锻过程中金属从坯料圆周部位沿挤压腔壁向中部流动，完成齿部填充。不同的挤压方式，材料的充填能力及模具的变形抗力也不同。

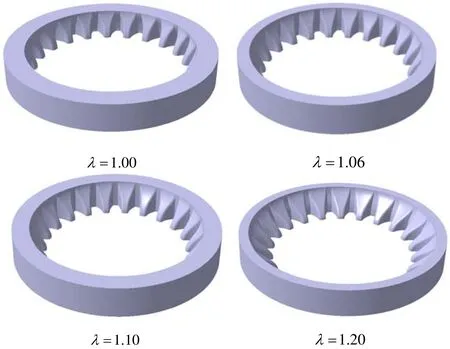
图4 不同放大系数的挤压腔模型

3.2 不同参数值模拟结果分析

（1） λ=1.2和λ=1.0的模拟结果

图5 λ=1.2 时凸、凹模z向等效载荷曲线

当λ为1.2，挤压方式为完全的正挤压。数值模拟的结果显示整个挤压过程中，坯料金属紧贴挤压腔壁流动，顺利完成了齿顶填充，但坯料所受变形力较大。图5是λ=1.2时凸模、凹模的z向等效载荷曲线。第60增量步（曲线的最右端）时，凸模z向载荷接近1300kN，凹模z向载荷接近900kN，基本上是其它几个模拟结果数值的两倍，而此时的载荷曲线仍有上升趋势。图6是坯料在挤压第40步时的应力分布，坯料与挤压腔接触的所有部分受力都较大，即便是已经成形的齿顶因为直径是在变小也始终处于受力状态，不符合本文精锻方案的设计初衷。

图6 λ=1.2 坯料在第40步时应力分布

当λ为1.0时，挤压方式为复合挤压，坯料半径小于分度圆半径，径向挤压深度较深。数值模拟结果显示整个挤压过程中，坯料所受变形力不大，但在450kN的反向力作用下，没有完成齿形的填充，齿顶存在明显缺陷。图7是λ=1时凸模、凹模的z向等效载荷曲线，凸模、凹模的z向等效载荷没有超过650kN和180kN，曲线走向平滑、过渡均匀，是比较理想的载荷曲线结果。但图8第60步挤压腔中部切片示意图显示坯料和挤压 腔之间有间隙，齿顶未被充满。

图7 λ=1.0时凸、凹模z向等效载荷曲线

图8 λ=1.0第60步中部切片示意图

综合以上分析说明本文方案在正挤压情况下，凸、凹模承受的冲击和磨损要比复合挤压情况下大得多，表明λ值不可取的过大，坯料直径不应大于齿顶圆半径。分析齿顶未被充满的原因，是因为坯料半径过小，径向挤压深度较深，需要的径向变形力较大，若要完成齿形的填充必须设定更大得反向力，来产生大的径向变形力。坯料面积和齿形面积完全相同的挤压腔，并不能达到良好的挤压效果。

图9 λ=1.06时凸、凹模z向等效载荷

（2） λ=1.06和λ=1.1的模拟结果

挤压腔λ=1.06和λ=1.1时的数值模拟结果是比较理想的结果。凸、凹模各向等效载荷都较低，整个挤压过程中坯料金属紧贴挤压腔壁流动，齿形填充情况良好，坯料变形力始终在600MPa以下，齿顶相对齿根部分受力较小，坯料成形部分齿形表面质量良好。

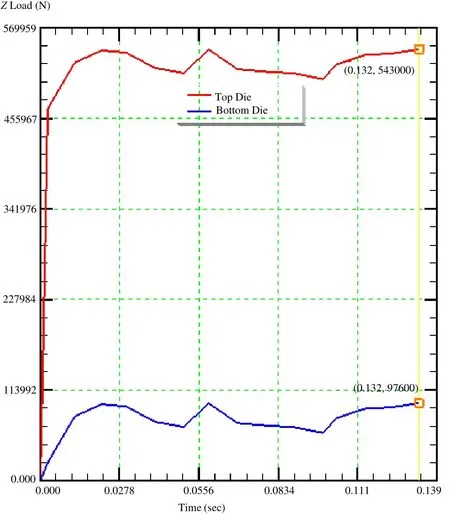
图10 λ=1.1时凸、凹模z向等效载荷

图9和图10是凸、凹模的z向等效载荷曲线，λ=1.1时凸、凹模z向载荷最大值分别为880kN和430kN，λ=1.06时凸、凹模z向载荷最大值分别为540kN和98kN，说明在相同的参数设定下，λ=1.06的挤压腔要比λ=1.1的挤压腔在挤压过程中凸、凹模的受力小很多。从应变情况来看，两个挤压腔应变分布相似，齿顶成形后应变较小，坯料应变大的区域都集中在齿根处。从应力分布来看，与应变分布相似，齿根区域受力较大，λ=1.06的挤压腔坯料受力要小一些。

4 挤压腔优化结论

从四个挤压腔的数值模拟结果来看，在相同的模拟参数下，除却λ=1.0的挤压腔外，其它参数的型腔都能顺利地完成齿形的填充，但坯料所用的变形力不尽相同，模具承受的冲击和磨损也有较大变化。

理论上，坯料面积和齿轮断面面积完全相同时，数值模拟结果应该有良好的填充能力、最小的变形力和最小的模具受力，但模拟结果显示，λ=1.0的挤压腔未能完成齿形的填充，且模具所受z向等效载荷比λ=1.06的挤压腔还要大一些，说明坯料直径过小会使齿根到齿顶的径向挤压深度过长，不但不利于齿形的填充，还会增大模具冲击和磨损。

其它三个参数值的挤压腔模拟结果都最后顺利地完成齿形的填充，坯料所受变形力和模具承受的冲击载荷和磨损随λ值的增大而变化。复合挤压方式下，即λ<1.11时，模具的等效载荷曲线过渡平滑，基本保持在一个恒定值范围内；而在正挤压方式下，模具的等效载荷曲线数值较高，且呈上升趋势，λ越大这种上升趋势就越明显，例如λ为1.2的挤压腔在第10步时，凹模的z向等效载荷已经高于了λ为1.06的挤压腔凸模的z向等效载荷，且到第60步还在增大。

综合以上分析说明，要使模拟结果具有好的齿形填充性能，低的坯料变形力和低的模具承受载荷，坯料放大系数λ不宜取的过大也不宜取得过小。将四个型腔模拟结果的凸、凹模z向等效载荷取最高值，用样条曲线将它们连接起来，得到了如图11所示的两条曲线，凸模载荷曲线和凹模载荷曲线基本相似，曲线最低点的横坐标都落在了1.06上，也就是说，λ为1.06的挤压腔，数值模拟结果有最低的模具承受冲击载荷和磨损，有良好的齿形填充性能，而λ为1.06挤压腔的数值模拟结果也证明了这一结果。λ=1.06是本文圆柱直齿轮冷挤压腔造型参数的最优解。

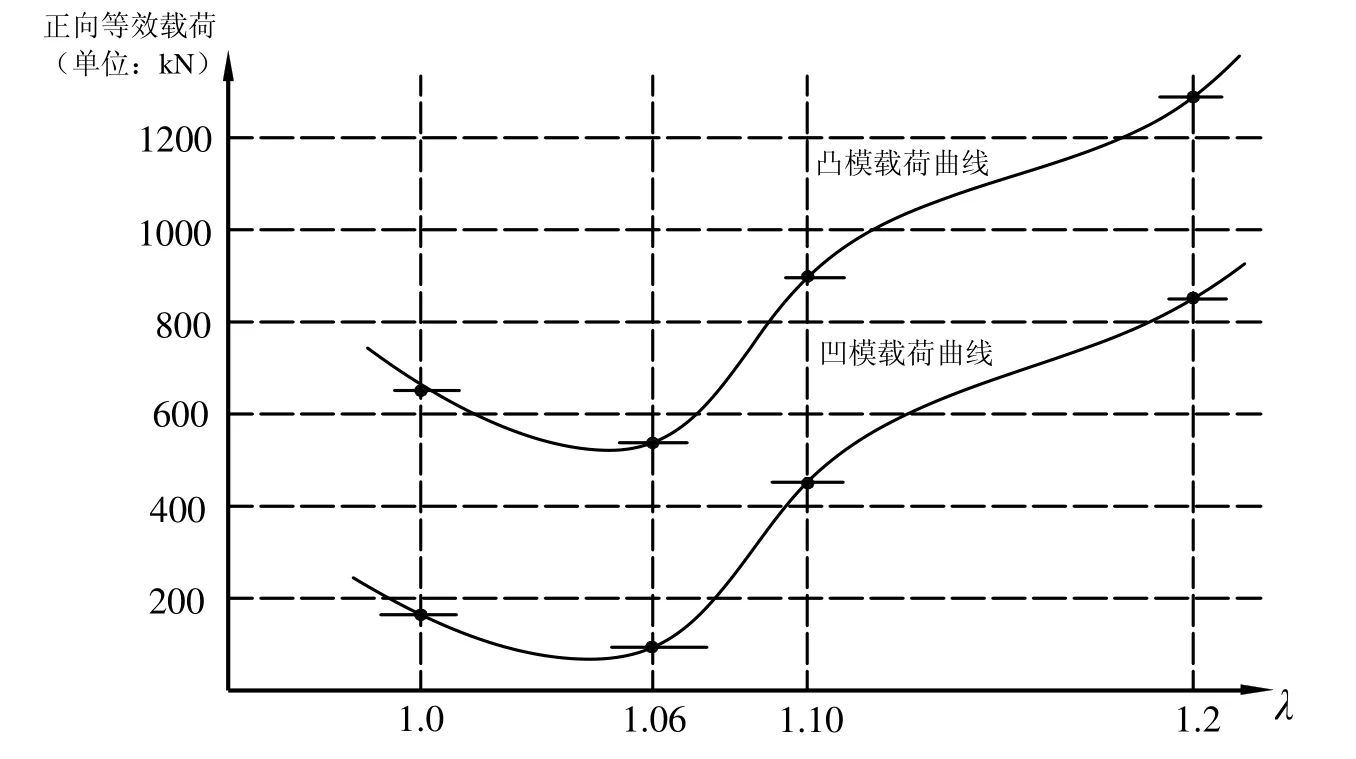
图11 不同参数下凸、凹模z向等效载荷最大值模拟曲线

[1]孟冠军, 屈新怀, 黄皖苏. 直齿圆柱齿轮连续预锻成形型腔构造[J]. 工程图学学报, 2007, 28(S1)：11-14.

[2]刘全坤, 李冬生. 基于流线型凹模型腔的直齿圆柱齿轮冷挤压数值模拟分析[J]. 工程设计学报, 2005,12(1)：15-19.

[3]孟冠军, 屈新怀, 丁必荣, 等. 基于预锻成形腔的直齿圆柱齿轮冷挤压数值模拟分析[J]. 工程图学学报,2009, 30(2)：86-90.

[4]刘 华, 席庆坡, 霍艳军, 等. 圆柱齿轮冷精锻数值模拟及其轮齿修形规律[J]. 西安交通大学学报,2004, 38(11)：245-248.

Parameter Optimization of Female Die Molding in Cold Extrusion of Spur Gear

MENG Guan-jun, ZHAO Han, CHEN Ke
( School of Mechanical and Automotive Engineering, Hefei University of Technology, Hefei Anhui 230009, China )

Aimed at the problems of great deformation force and hard corner filling in cold extrusion of spur gear, a geometry model of the streamline female die of spur gear is constructed, based on which numerical simulation of cold extrusion of spur gear is conducted.The results indicate that the streamline female die is effective in improving metal filling in corner under small deformation force. By analyzing the influence of different blank magnifying radius (namely λ) on female die shape and deformation mode in the simulation process, the parameter value of λ for a most optimized model is found through numerical simulation of different female dies.

mechanical manufacture; parameter optimization; numerical simulation; spur gear

TG 376.2

A

1003-0158(2010)06-0100-06

2009-06-12

合肥工业大学科学研究发展基金资助项目（070203F）

孟冠军（1979-），男，安徽临泉人，讲师，博士研究生，主要研究方向为现代集成制造，CAD/CG。