三维重建中的剖视图处理

王 翔， 丁运亮， 李 静

（1. 南京航空航天大学航空宇航学院，江苏 南京210016；2. 南京航空航天大学自动化学院，江苏 南京210016）

三维重建中的剖视图处理

王 翔1， 丁运亮1， 李 静2

（1. 南京航空航天大学航空宇航学院，江苏 南京210016；2. 南京航空航天大学自动化学院，江苏 南京210016）

剖视图处理能够有助于更好地理解视图，提高三维重建的效率。基于对剖视图自身特点的分析，提出了三维重建中对剖视图的处理算法，即通过剖视图信息的智能提取生成基元体，将基元体同由视图轮廓生成的参照体进行布尔运算，从而得到最终的目标体。算法能够处理包括全剖视图、半剖视图以及平行剖视图在内的剖视图，最后给出了应用算例以验证算法的可行性。

工程图学；计算机辅助设计；三维重建；剖视图

在工程视图中存在着大量的剖视图，剖视图的引入消除了视图表达的歧义性，便利了视图的理解，但却增加了三维重建的难度，这是缘于剖视图信息同一般投影视图信息有着本质上的差异，剖视图在工程视图理解中提供的是示意信息，它的理解依赖于局部的三维形状，具有局部整体性，其表达的信息较为隐含，其约束也具有一定的模糊性。如何将剖视图中隐含的投影信息正确地提取出来，并将其转化为三维重建能够理解的正交视图是三维重建中剖视图处理的核心环节。

三维重建工程中对于剖视图的研究为数甚少，Markowsky和Wesley[1]在他们的线框算法中最早研究了剖视图存在的情况，他们提出当正交视图中存在剖视图时，所生成的三维候选顶点需满足位于剖切平面和投影方向所确定的半空间中这一条件，由于剖视图会产生大量的多余候选点，从而增加了错解发生的几率。Geng[2]在重建算法中引入了人工智能的思想，模仿工程师的识图方法，采用了分层重建的策略，将实体在不同的位置进行截切，当出现形状同投影不一致的情况时，便使用剖视图代替该截面，在这里剖视图只是作为三维重建的辅助手段，并未作为主要研究对象。Aldefeld[3]和 Bin[4]的算法也将剖视图考虑在内，但是大量的人工介入使得程序的效率大打折扣。Dimri[5]采用 CSG重建的策略对剖视图进行了深入的研究，算法首先识别出剖视图同投影视图中不同的边以及闭环，通过投影匹配生成子实体，最终由布尔运算生成目标实体。能够处理全剖、半剖的情况，但是仅限于投影视图中存在单一剖视图的情况，多幅剖视图并存的情况则无法解决。

本文在深入分析剖视图自身特点的基础上，找出了剖视图同一般投影视图的不同之处，从这些差异点着手，提出了三维重建中针对剖视图的处理方法。

1 剖视图简介

当用普通投影视图无法完全表达实体的内部结构时，往往采用剖视图作为辅助表达手段。它是假想用一剖切面剖开实体，将处在观察者和剖切面之间的部分移去，而将其余部分向投影面上投影，这样得到的投影视图即为剖视图。按照剖切范围的大小可以分为全剖、半剖以及局部剖视图，按照剖切平面和剖切方法可分为平行剖、移出剖、以及旋转剖等。分别图示如下。

（1） 全剖视图

用剖切面完全贯穿实体所得的剖视图称为全剖视图。全剖视图用于外形简单，内部结构较复杂且不对称的实体。如图1所示即为全剖视图。

图1 全剖视图

（2） 半剖视图

当实体具有对称平面时，向垂直于对称平面的投影面上投射所得的图形，可以对称中心线为界，一半画成剖视图，另一半画成普通投影视图。这样的表达方法获得的剖视图称为半剖视图。如图2所示即为半剖视图。

图2 半剖视图

（3） 局部剖视图

用剖切面局部地剖开实体，一部分画成普通投影视图以表达外形，其余部分画成剖视图以表达内部结构，这样所得的图形称为局部剖视图。例如，有盲孔存在时多采用局部剖视图，如图3所示。

图3 局部剖视图

（4） 平行剖视图

当需要表达实体中分布在几个相互平行的平面上的内部结构时，可采用几个平行的剖切面剖开实体的表达方法，即平行剖视图，如图4所示。

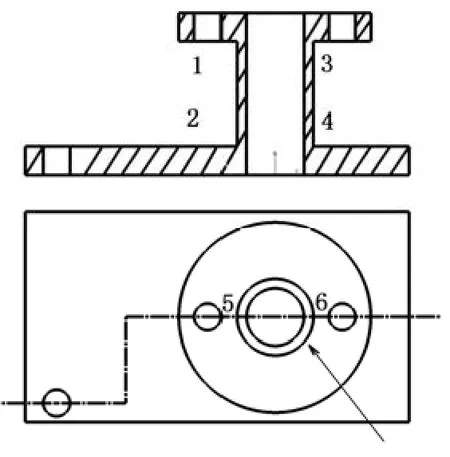
图4 平行剖视图

（5） 移出剖视图

将实体从某些特殊位置剖切开，并将剖视图移出主视图，该类剖视图被称为移出剖视图，轴类零件常用此类剖视图表示，如图5所示。

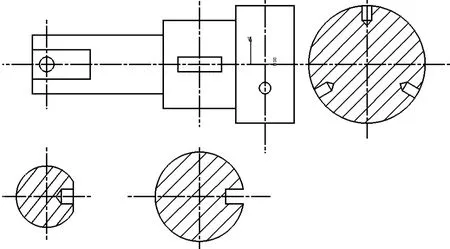
图5 移出剖视图

（6） 旋转剖视图

将实体在某一位置剖切开，将剖面图旋转90°，此类剖视图即为旋转剖视图，如图6所示。

图6 旋转剖视图

2 定义及术语

以下是算法中用到的一些概念定义和名词术语，大部分来自Soni & Gurumoorthy[6]。

（1） 面 环

由一系列闭合的边围成的区域。如图7View1中的面环{5, 6, 9, 10, 5}。

图7 匹配点与匹配环

（2） 切 点

如果两条边在某处相交，并保持一阶连续，该点即为切点，切点有直线与直线的切点、直线与曲线的切点以及曲线与曲线的切点之分，后两者在切点处曲率保持一致，直线与直线的切点实质上是边的内部点，如图 7View1中的点 5，就是直线段6－7与5－6的切点。

（3） 轮廓点（重影点）

垂直于某一投影面的边会在该投影面内积聚为一点，该点即为轮廓点，如图7View1中的点1，2。

（4） 极限点

在面环内具有极限位置的点，如图 7View1中的点 7，4分别是面环{4,5,6,7,8,3,4}的左右极限点。

（5） 面环的包含关系划分

两个面环L1和L2，如果面环 L1的所有边均在面环L2内，则称L1为L2的内环，L2为L1的外环，如果L1中有的边在L2内部，有的边在L2上，则称 L1为 L2的内交环，如果 L1中有的边在 L2内部（或边界），有的在 L2外部，称 L1为 L2的外交环。如图7View1中的环{1, 2, 1}是环{4, 5, 6,7, 8, 3, 4}的内环，环{5, 6, 9, 10, 5}是环{4, 5, 6, 7,8, 3, 4}的内交环，View2中的环{4, 5, 6, 12, 11, 3}是环{1, 10, 9, 8, 7, 6, 12, 11, 3, 2, 1}的外交环。

（6） 实环与虚环

组成面环的边均为实线称为实环，反之若环面的所有边均由虚线组成则称该面环为虚环。实环对应的是实体部分，虚环对应的则是孔、洞等虚体。

（7） 匹配点

两投影视图中沿某一公共坐标轴具有相同坐标的点称为匹配点，一个点可以有多个匹配点。如图7View1中的点3在View2中的匹配点为点1和点2。

（8） 匹配面环

（9） 基元体

所有匹配的面环沿垂直于投影面的方向平扫，得到的平扫体求交后生成的实体即为基元体。基元体之间作交、并、差等布尔运算便可得到最终重建实体。

3 算法概述

3.1 预处理

工程视图采用.DXF格式输入，由于大多数情况下，多个投影视图位于同一幅图中，即同一图层内，这样很难从中得到图元所属视图的信息，因此必需将图元所属的投影视图划分开来，即视图的分割。视图的分割是基于如下性质进行的：每一个独立视图都应是连续、封闭的图元组合，任何穿过视图的直线必然与该视图中的图元相交或重合。对分割后的视图进行坐标系转换，将设备坐标系转换成投影坐标系。进行坐标系转换后的投影视图，还需进行图素的拼接和打断处理[2]。经过上述预处理工作后，得到了一系列数据关系结构，其中包括图元和所属视图关系链表，点边关系链表等。以上得到的全部作为三维重建的输入。

3.2 布尔运算

将投影视图的轮廓进行平扫求交生成当前参照体，对提取出来的所有边使用极左邻边搜索法[7]生成一系列的面环，由面环平扫求交得到一系列基元体，依次将基元体同当前参照体进行实体布尔运算，即不断刷新当前参照体，当参照体视图投影同初始视图完全匹配时，算法结束。算法流程如图8所示。

图8 算法流程图

4 剖视图处理

算法的核心环节在于如何对投影视图中的剖视图进行恰当的处理。由于剖视图不同于普通的投影视图，因而需对其作特殊处理。

（1） 剖视图是完全独立的视图，对其它视图没有任何影响，但有时可以利用剖视图提供的视图信息擦除其它视图中不必要的图元，以达到简化视图的效果。如图9中所示的主视图采用剖视图表示，左视图中的两条虚线在擦除后仍不影响视图的完整表达，类似情况可作擦除处理。

图9 剖视图处理示例

（2） 被剖切平面遮挡的部分，虚线一般省略，但是一些特殊情况下需要画出，如图 10所示的剖视图中的虚线，如果不画则不能确定孔和楔块是否存在。

图10 剖视图中含有虚线的情况

（3） 在半剖视图中的非剖切部分的虚线可作擦除处理。

上述3种情况中之所以可以对视图中的虚线作擦除处理，是因为在生成基元体的过程中，往往不需要3个投影均完备，有时只需一个反映基元体特征的特征投影和一个辅助投影即可。经擦除处理后，可以生成较少的面环，从而避免多余基元体的生成。

（4） 同上面的面环过多情况不同的是，有时现有的面环不能满足生成基元体的条件，在这种情况下则需要补充额外的面环，例如图 11中所示的情况，正视图中的面环{1,2,3,4,1}在左视图中找不到与之相匹配的面环，但是如果把左视图中的 3个面环{5,6,7,8,5}、{7,8,9,10,7}以及{9,10,11,12}合并成为一个面环{5,6,11,12,5}，那么该面环便可以和正视图中的{1,2,3,4,1}以及俯视图中的{13,14,15,16,13}组成匹配的面环。

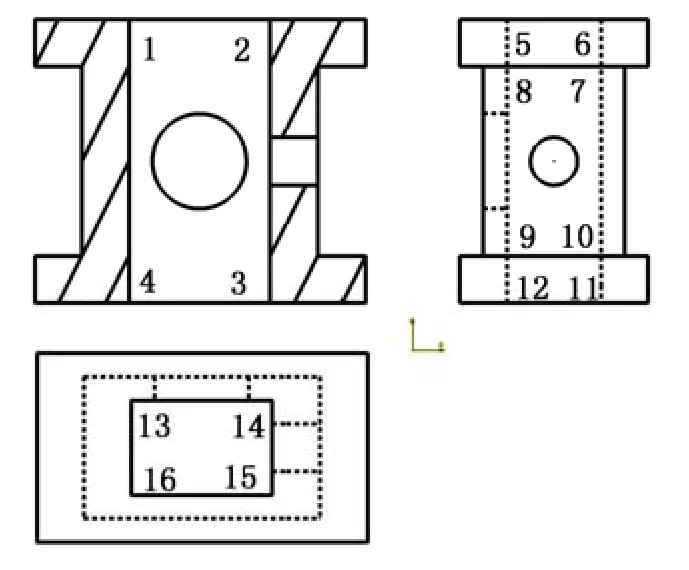
图11 面环的合并

（5） 如果视图中存在仅通过虚线同其它面环相连接的面环，那么将该面环视为孤立的面环。如图 12中所示的箭头所示的面环仅同两条虚线相连，很显然该面环同两条虚线所代表的实体部分具有着不同的深度信息，即两者不可能从属于同一基元体，故可将该部分孤立开来，单独处理。

图12 孤立的面环

（6） 视图中孤立的环面大多为孔洞或拉伸结构体，对于这类结构，在生成基元体时不需要3个视图投影，而只需要两个即可，这种情况下将第3个视图中匹配的面环删除来减少运算量。

（7） 如果对于一个孤立的面环，在剖视图中无法找到与之相匹配的面环，在这种情况下，只需找到与之相匹配的边即可，将孤立面环沿这些边平扫便可得到基元体。如图4中箭头所指的孤立面环在剖视图中无法找到与之匹配的面环，那么转而搜索面环中的极限点，在这里是点5，6。恰巧这两点又都是轮廓点，分别对应于剖视图中的边1-2和3-4，并且边1-2和3-4长度相同，于是将面环{5,6,5}沿1-2方向平扫即可得到基元体。

（8） 生成的基元体可以分为实体和虚体两大类，分别对应的实体生成操作为镗孔和拉伸，为确定操作的类型，算法将基元体反投影回各个视图，通过对比投影同初始视图的轮廓的位置关系来确定实体还是虚体。由基元体投影得到的面环称为目标环，选取目标环中连接度大于2的点作为初始点开始回溯，如图 13所示，主视图中面环{1,2,3,4,1}为目标环，环{1,2,3,4,5,6,7,8,1}为由投影轮廓生成的外环，点1为初始点，同它相连的三条边分别为‘a’，‘b’，‘c’，具体算法如下：

图13 目标环与外环

当基元体被判断为虚体时，需要将外环同目标环进行合并操作，合并意味着外环和目标环中的边之间需要进行交或并运算。令Le表示外环，Lt表示目标环，Lm表示合并后的面环。则合并运算需满足下面的公式[8]

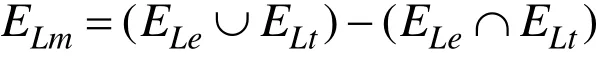
例如，图7 View1中的环{3, 4, 5, 6, 7, 8, 3}同{5, 6, 9, 10, 5}合并后得到{3, 4, 5, 10, 9, 6, 7, 8,3}。合并后得到的新环将用来更新原有的外环，故由此可得到相应的算法，具体如下：外环（）

5 结果及讨论

5.1 重建算例

算例程序采用VC++6.0编写，OpenGL环境下运行。图14中所示的实体三视图如图11所示，其中图 14(a)为提取三视图轮廓，经平扫求交生成的初始当前参照体，将图 14(b)中的实体与图14(a)中的实体进行布尔运算，最后得到图 14(c)中的目标实体，其三视图同图 11完全匹配，即为重建实体。

图14 含全剖视图的三维重建算例

图 15(a)中的实体是以图 4为三视图的含阶梯剖视图的重建实体，图15(b)则是以图12为三视图的重建实体，算法同图14中的算例。

5.2 结果讨论

本文在对剖视图内在机理进行深入分析以及同普通投影视图对比的基础上，提出了剖视图的处理算法，并结合三维重建的工程实际进行了算例验证，如算例所示，算法能处理包括全剖、半剖，以及阶梯剖在内的剖视图。对于局部剖视、重合剖视等更为复杂的剖视图有待进行更深入的研究。

[1]Wesley M A, Markowsky G. Fleshing out projections [J].IBM Journal of Research & Development, 1981, 25(6)：934-954.

[2]Geng W D, Wang J B, Zhang Y Y. Embedding visual cognition in 3D reconstruction from multi-view engineering drawings [J]. Computer-Aided Design,2002, 34(4)：321-336.

[3]Aldefeld B. On automatic recognition of 3D structures from 2D representations [J]. Computer-Aided Design,1983, 15(2)：59-64.

[4] Bin H. Inputting constructive solid geometry representations directly from 2D orthographic engineering drawings [J]. Computer-Aided Design,1986, 18(3)：147-155.

[5] DIMRI J, GURUMOORTHY B. Handling sectional views in volume-based approach to automatically construct 3D solid from 2D viewsn [J].Computer-Aided Design, 2005, 37(5)：485-495.

[6]Soni S, Gurumoorthy B. Handling solids of revolution in volume-based construction of solid models from orthographic views [J]. Journal of Computing and Information Science in Engineering, 2003, (3)：250-259.

[7]GONG J H, ZHANG H, ZHANG G F, et al. Solid reconstruction using recognition of quadric surfaces from orthographic views [J]. Computer-Aided Design,2006, 38(8)：821-835.

[8]CHEN D X. Technical drafting and CAD elements [M].Mechanical Industry Press, Beijing：2004. 13-19.

Cutaway View Processing in 3D Solid Reconstruction

WANG Xiang1, DING Yun-liang1, LI Jing2
( 1. College of Aerospace Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing Jiangsu 210016, China 2. Automation College, Nanjing University of Aeronautics and Astronautics, Nanjing Jiangsu 210016, China )

Through providing extra information, cutaway view aids engineering view understanding and accelerates the 3D reconstruction process. This paper proposes a processing algorithm in 3D reconstruction based on the analysis of cutaway view features：to use the cutaway view information to intelligently fetch the basic entity, then to conduct Boolean operation on the basic entity and the reference object generated from view silhouette, and in this way to get the target object. The algorithm can process full cutaway views, half cutaway views and parallel cutaway views. Examples are provided to identify its feasibility in the paper.

engineering graphics; computer aided design; 3D reconstruction; cutaway view

TP 391

A

1003-0158(2010)06-0068-07

2009-02-27

国家自然科学基金资助项目（10377007）

王 翔（1981-），男，山东济南人，博士研究生，主要研究方向为计算机图形学、三维重建。