与给定多边形相切的可调二、三次Bézier曲线

刘 植， 檀结庆， 陈晓彦， 张 莉， 时 军

（1. 合肥工业大学计算机与信息学院，安徽 合肥 230009；2. 合肥工业大学数学系，安徽 合肥 230009）

与给定多边形相切的可调二、三次Bézier曲线

刘 植1,2， 檀结庆1,2， 陈晓彦2， 张 莉1,2， 时 军2

（1. 合肥工业大学计算机与信息学院，安徽 合肥 230009；2. 合肥工业大学数学系，安徽 合肥 230009）

讨论与给定多边形相切的分段二、三次Bézier曲线，所构造的曲线C1连续，且对切线多边形是保形的。曲线上的所有 Bézier曲线段的控制点由切线多边形的顶点直接计算产生。在一定范围内，可以通过调节控制参数对切线多边形作整体或局部逼近。实例表明，该文方法计算简单、控制灵活，方便有效。

计算机辅助几何设计；切线多边形；Bézier曲线；C1连续；保形

Bézier曲线具有许多优良的性质，在诸多形式的参数多项式曲线中独树一帜，被广泛的应用于计算机辅助几何设计(CAGD)和图形学(CG)等领域。近年来，人们对Bézier曲线的研究仍在不断深入。出于汽车制造业中汽车顶部，挡板等部件对曲面曲率和挠率的设计要求，Mineur[1]，Farin[2]，Cao等[3]讨论了一类带单调曲率和挠率的Bézier曲线。Kim等[4]构造了圆弧的四次Bézier逼近方法，通过分段，利用该方法可以得到圆弧的曲率连续的样条逼近。为了更加灵活的实现交互设计，Han等[5]提出了一类带形状参数的广义Bézier曲线曲面，作为Bézier曲线曲面的推广，除具备Bézier曲线曲面的优点外，通过调控形状参数的取值可以生成更加丰富的曲线曲面。为了扩大自由型曲线曲面的选择范围，汪志华等[6]提出了一族介于Bézier曲线与Wang-Ball曲线之间的新型曲线，并在形式上将 Bézier曲线与Wang-Ball曲线统一起来。

1983年Hering[7]首次提出与给定多边形相切的分段光滑闭曲线构造问题，并给出了其应用背景：带有两个固定非圆轮的链轮驱动的数学描述，两轮之间有定长的传送带和给定的非常数速率，求这两轮轮廓线的数学表示导出了一个非线性函数方程组，准确地求解这个问题似乎是毫无希望的。然而，可以用动力学方法将方程组转化为切线系（即一平面凸多边形），然后再构造与每边相切的保凸曲线，并至少满足整体C1连续，即为所求轮廓线的逼近曲线。此外，在服装CAD纸样的设计过程中，通常先根据尺寸要求确定控制点，再根据控制点用直线段绘制样片的大体轮廓，即控制多边形，然后在控制多边形内用直线和曲线绘制封闭的图形。由于样片的形状不规则，因此构成样片的曲线比较复杂，为了使曲线光顺、丰满、有弹性，且易于修改，也经常遇到与控制多边形相切的曲线构造问题[8]。围绕该问题人们进行大量的研究，利用不同方法构造了各种类型的曲线[9-10]。在构造与给定多边形相切的Bézier曲线问题中，也取得了一定的成果。Hering首先构造了与给定多边形相切的 C2连续分段三次Bézier曲线，但该方法计算量较大，生成的曲线不具有保形性，且不能做局部修改。1991年方逵[11]改进了Hering的方法，构造的G2连续分段三次 Bézier曲线基本上克服了 Hering方法的缺点，但切点的控制不够灵活，局部修改仍然较复杂。此后方逵[12]继续研究了 C2连续分段四次和C3连续分段五次Bézier曲线，但四次曲线只能依靠调整切点来控制曲线的形状，而五次曲线不能做局部修改，且次数较高。低次Bézier曲线具有形状简单、使用灵活等优点，应用广泛。而构造与给定多边形相切的低次 Bézier曲线在诸文献中尚不多见。

本文讨论了与给定多边形相切的分段二次及三次Bézier曲线，构造的曲线具有保形性，在一定范围内，通过改变控制参数的取值，可以灵活调控切点及内Bézier点的位置，从而改变曲线的形状，且曲线整体满足C1连续。

1 与给定多边形相切的分段三次Bézier曲线

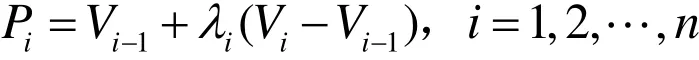
其中 控制参数 λi( i = 1 ,2,… , n )满足0 ＜ λi＜1。将在每相邻两切点 Pi, Pi+1之间构造一段三次Bézier曲线

其 中 控 制 参 数 μi(i = 1,2,… ,n +1)满 足0 ＜ μi≤ min{λi, 1 - λi} ,μn+1=μ1， 分 别 称λi, μi(i = 1,2,… ,n +1)为切点调节参数和内Bézier点调节参数。由式(1)可知，第i段与第 i +1段曲线的Bézier点满足：

根据三次 Bézier曲线的端点性质，对i = 1 ,2,… ,n ，容易验证

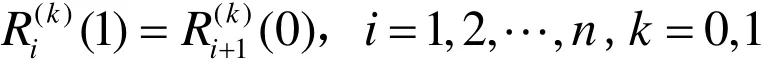
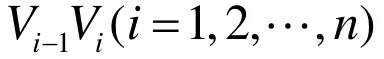
图1 三次Bézier曲线的控制点

事实上，根据参数 {λi, μi的取值范围可以看出，构成的凸三边形与Vi-1, Vi, Vi+1构成的凸二边形凸性相同。由Bézier曲线的保凸性知， Ri( t)是凸的，且凸性与Vi-1, Vi, Vi+1构成的凸二边形相同。设 Vi是切线多边形的一个转折点，即矢量 Vi-2Vi-1×Vi-1Vi与Vi-1Vi× ViVi+1方向相反，则第 i - 1段Bézier曲线Ri-1(t )与第i段 Bézier曲线 Ri( t)的凸性相反，且在切点 Pi处产生一个拐点。因此，构造的曲线拐点个数与切线多边形的转折点个数相等，故分段曲线对切线多边形是保形的。

曲线的计算步骤：

对于给定开的多边形，用上述方法也可以构造与开多边形每边都相切的分段三次 Bézier曲线，且曲线对多边形保形，整体C1连续，如图1所示。

2 与给定多边形相切的分段二次Bézier曲线

下面考虑与给定多边形相切的分段二次Bézier曲线，即生成的曲线在满足上述分段三次Bézier曲线特点的基础上，次数降为二次。

由于次数的降低，Bézier曲线的控制自由度随之减少，对控制多边形的表现力下降。根据二次Bézier曲线的端点性质，在给定多边形相邻两边之间构造一段二次 Bézier曲线，且满足整体C1连续，切点只能位于给定多边形各边的中点，

图2 二次Bézier曲线的控制点

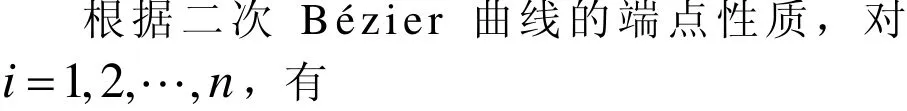
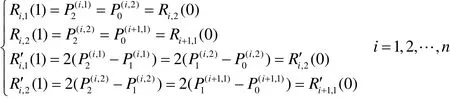
曲线的计算步骤：

对于给定开的多边形，用上述方法也可以构造与开多边形每边都相切的分段二次 Bézier曲线，且曲线对多边形保形，整体C1连续，如图2所示。

3 数值例子及结论

图3 参数 λ i , μi取不同值时的二次逼近曲线

图4 参数 λ i , μi 取不同值时的三次逼近曲线

例 2 设平面四边形顶点为 V0=(-1,- 1 )，V1=(-1 ,1), V2= ( 1,1), V3= ( 1,- 1 )。考虑到对称性，取控制参数 λi=0.5, μi=0.275, i =1,2,3,4，得到单位圆的 C1三次逼近曲线。取控制参数λi=0.5, μi=0.207, i=1,2,3,4，得到单位圆的C1二次逼近曲线。图5(a)、图5(b)分别给出了第一象限四分之一单位圆的逼近曲线。用文献[4]的方法可以构造该问题的四次Bézier逼近曲线，如图5(c)所示。

图5 四分之一单位圆的Bézier逼近曲线比较

通过调整控制参数的取值可以生成不同的逼近曲线。经过计算可知，例2中三种逼近曲线段与圆弧段的 Hausdorff距离（即圆半径的最大逼近误差）分别为 3 .1× 1 0-3，1 .4 × 1 0-5，2 .0 × 1 0-6，尽管本文方法的误差较文献[4]方法大，但计算量显然要小得多，而在误差允许的范围内，三次Bézier逼近曲线也不失为一个较满意的结果。

本文讨论了与给定多边形相切的分段二次及三次Bézier曲线，构造的曲线具有保形性，在一定范围内，通过改变控制参数的取值，可以灵活调控曲线的形状，整体满足 C1连续。与现有方法相比，本文方法具有次数低、计算量小、控制灵活等优点。

[1]Mineur Y, Lichah T, Castelain J M, et al. A shape controlled fitting method for Bézier curves [J].Computer Aided Geometric Design, 1998, 15(9)：879-891.

[2]Farin Gerald. Class a Bézier curves [J]. Computer Aided Geometric Design, 2006, 23(7)：573-581.

[3]Cao Juan, Wang Guozhao. A note on class a Bézier curves [J]. Computer Aided Geometric Design, 2008,25(7)：523-528.

[4]Seon-Hong Kim, Young Joon Ahn. An approximation of circular arcs by quartic Bézier curves [J].Computer-Aided Design, 2007, 39(6)：490-493.

[5] Han Xi-an, Ma Yichen, Huang Xili. A novel generalization of Bézier curve and surface [J]. Journal of Computational and Applied Mathematics, 2008,217(1)：180-193.

[6]汪志华, 朱晓临. Bézier曲线与Wang-Ball曲线的统一表示[J]．计算机辅助设计与图形学学报, 2008,20(7)：888-893.

[7]Hering L. Closed (C2-and C3-continuous) Bézier and B-spline curve with given tangent polygons [J].Computer-Aided Design, 1983, 15(1)：3-6.

[8]姜 卫. 服装CAD[M]. 上海：中国纺织大学出版社,1999. 36-75.

[9]方 逵, 谭建荣, 赵 军. 带有给定切线多边形的保形有理三次B-样条曲线[J]. 工程图学学报, 1996,(2)：99-105.

[10]王成伟. 与给定多边形相切的C3连续B3样条曲线[J].工程图学学报, 2002, 23(1)：104-108.

[11]方 逵. 与给定多边形相切的闭(G2-连续)Bézier曲线[J]. 计算数学, 1991, 13(2)：34-37.

[12]方 逵, 蔡 放, 谭建荣. 带有给定切线多边形的C2和 C3Bézier闭样条曲线[J]. 计算机辅助设计与图形学学报, 2000, 12(5)：330-332.

Adjustable Quadratic and Cubic Bézier Curves with Given Tangent Polygons

LIU Zhi1,2, TAN Jie-qing1,2, CHEN Xiao-yan2, ZHANG Li1,2, SHI Jun2
( 1. College of Computer and Information, Hefei University of Technology, Hefei Anhui 230009, China;2. Department of Mathematics, Hefei University of Technology, Hefei Anhui 230009, China )

This paper proposes an approach to constructing planar piecewise quadratic and cubic Bézier curve with all edges tangent to a given polygon and the curve segments are joined together with C1-continuity. The segmented Bézier curves are all shape preserving to their tangent polygon. All control points of the Bézier curve segments can be calculated simply by the vertices of the given polygon. The curve can locally or globally approximate the tangent polygon by the adjustment of the control parameters. Experiments show that the method given in this paper is simple, intuitive, effective and easy to control.

computer aided geometric design; tangent polygon; Bézier curve; C1-continuity;shape preserving

TP 391

A

1003-0158(2010)06-0045-06

2009-02-12

国家自然科学基金资助项目（60773043）；教育部博士点新教师基金资助项目（2008JYXJ0828）；安徽省自然科学基金资助项目（070416273X）；安徽省高校优秀青年人才基金资助项目（2009SQRZ008）；合肥工业大学科研基金资助项目（071003F）

刘 植（1976-），男，安徽金寨人，讲师，博士研究生，主要研究方向为数值逼近，CAGD等。