在机检测中STL格式自然二次曲面特征参数的提取
2010-09-25郑惠江王太勇何改云郝永江
郑惠江,王太勇,何改云,郝永江
(天津大学天津市先进制造技术与装备重点实验室,天津 300072)
在机检测系统使加工中心在原功能的基础上增加了产品质量检测的功能,建立起无需脱离生产环境即可完成加工—检验—再加工的复杂空间型面CAD/CAM/CAQ闭环制造系统(CAD—computer aided design,计算机辅助设计;CAM—computer-aided manufacturing,计算机辅助制造;CAQ—computer aided quality,计算机辅助质量管理).而从 CAD 数据中提取加工零件的几何特征参数进行测量轨迹的规划,是在机检测系统实现其基本功能的重要基础之一.
本文基于 STL文件中三角面片法向量的高斯映射提出一种对工件模型中自然二次曲面特征的判定方法,并通过将快速聚类法和 Gauss-Newton法相结合,研究了不同类型曲面几何特征参数的提取方法.
1 自然二次曲面几何特征的判别
如图1所示,考虑到实体造型中出现不完整自然二次曲面及 STL格式文件本身记录数据存在误差等情况,将组成圆柱表面的三角面片的法向量进行高斯映射[5-6],在单位球面上形成一个在大圆附近的、具有较小宽度的圆带(或部分圆带).组成圆锥面(圆台面)的三角面片的高斯映射,在单位球面上形成一个小圆附近的、具有较小宽度的圆带(或部分圆带);球面的高斯映射为一个单位球面(或部分球面);平面的高斯映射在单位球面上形成一个投影点附近的较小区域.将STL模型记录的三角面片法向量,利用最小二乘法进行平面拟合.平面方程用 ax+by+cz+d=0表示,通过求解线性方程组 0=Ax 拟合平面,其中
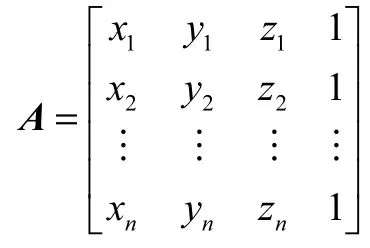
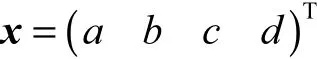
建立方程 ATAx =0,求解 ATA最小特征值对应的特征向量,即求得拟合平面方程系数(a b c d),令,则拟合平面的单位法向量为nˆ =(a ′b′c′).该平面相对于高斯球球心的距离为d′.计算各个三角面片法向量相对拟合平面带有符号的距离δi[7],
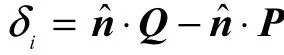
式中:Q为所计算的法向量;P为拟合平面上的一点.
对于给定的阈值δ′,若存在多个δi>δ′,则判定该表面为球面;当 δi< δ′时,若d′− 1 < δ ′′(δ′为给定的阈值),则给定表面为平面;若d′− 0 < δ ′′,则给定表面为圆柱面;若d′−1> δ ′′且d′− 0 > δ ′′,则给定的表面为圆锥面(圆台面).δ′和δ′的大小与 STL格式文件的数据精度有关,从工程实际应用情况出发,可以选择δ′= δ′= 0.001.
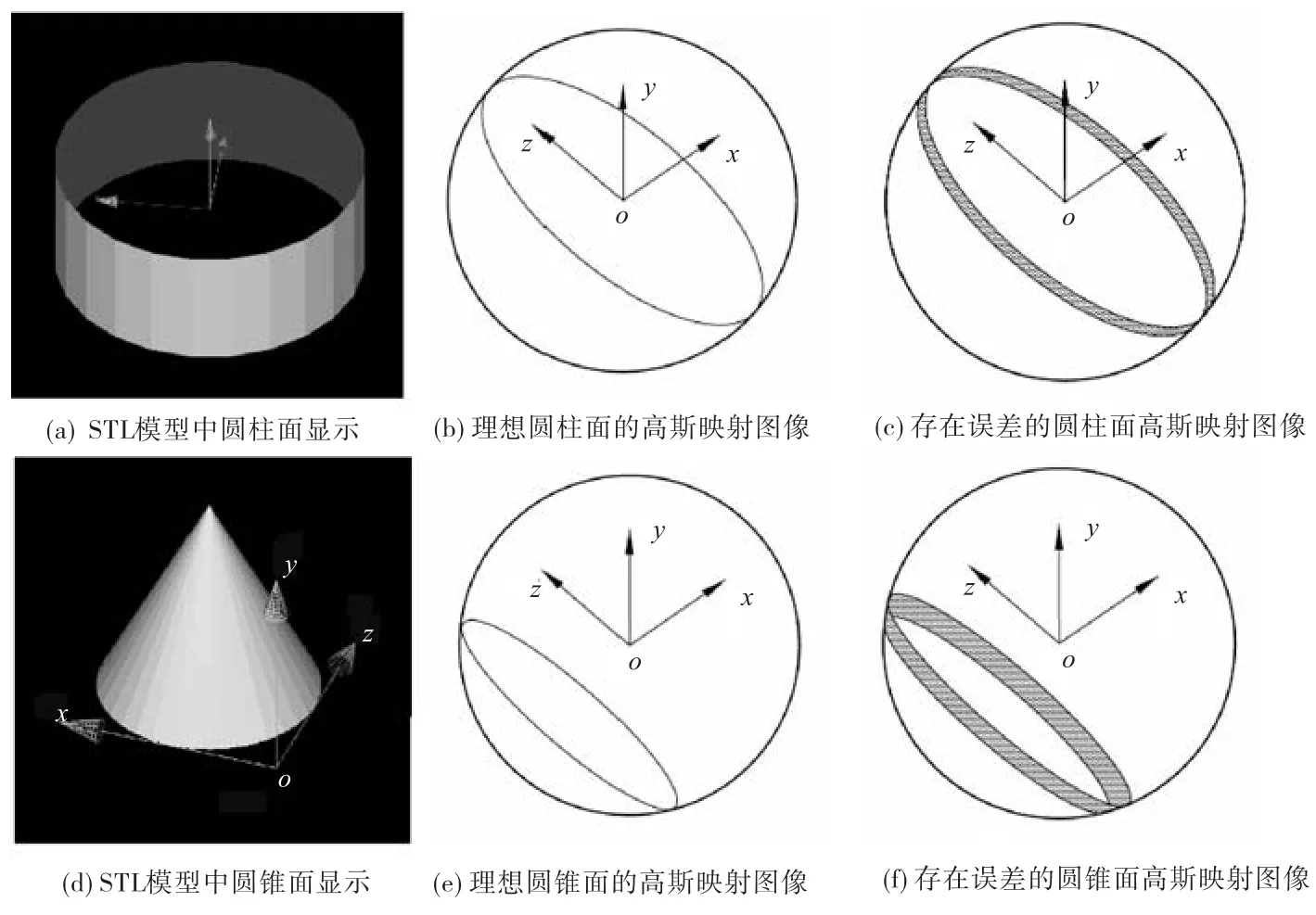
图1 STL模型及其高斯映射图像Fig.1 STL models and their Gaussian images
2 自然二次曲面特征参数的提取
在判定出所给定的几何表面形状后,即可按其形状特点,对 STL模型中给定几何表面上坐标点的坐标进行自然二次曲面特征参数的提取.
2.1 球面特征参数的提取
球面的特征参数主要是球半径 r.球面可用方程x2+ y2+ z2+ asx + bsy + csz + ds= 0 来表示,可采用奇异值分解法求解线性方程组 A xs=Bs来拟合球面,得到球面方程的系数 xs=(asbscsds)T[8].其中A同平面拟合中的A,而
忽然,树枝摇晃起来,叶子上的水落下来,洒了秀容月明一身。秀容月明惊讶得抬起头,他看到了一颗颗黑紫色的桑枣,也看到树丫上坐着一个少女,赤着脚,一双亮晶晶的眼睛正盯着他,看他湿淋淋的样子,少女咯咯咯地笑起来。
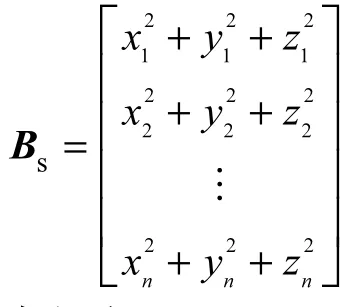
则球面半径为
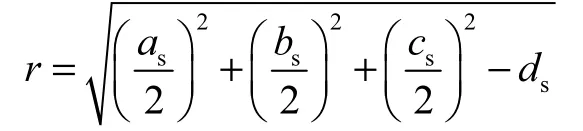
2.2 圆锥面特征参数的提取
圆锥面的特征参数主要是锥面高度、大底圆半径和锥顶角.如图 2所示,圆锥面向垂直于其回转轴线的平面投影得到的是一个圆环或者部分环面扇形.

图2 圆锥面在与其回转轴线垂直平面上的投影Fig.2 Projections of the circular conical surface on the plane squaring to their spin axes
圆锥面上的各点到该平面带有方向的最大距离和最小距离之差即为该圆锥面的高度,其锥角θ=2arcsind′.
如图3所示,圆锥面投影中的小圆和大圆之间分布的三角片数目较为均匀,坐标点的分布密度小圆要大于大圆,利用相邻两坐标点之间的距离,采用快速聚类法[9]对坐标点分类识别,识别出属于大底圆的坐标点.设集合S为{xi,i = 1 ,2,… ,n },其中 xi为STL文件中圆锥面上所有的坐标点.以 xi与其相邻坐标点间的最小距离()作为样本进行聚类分析,


图3 STL模型中圆锥面上坐标点分布情况Fig.3 Distribution of coordinate points on circular conical surface in STL model
选定样本值中的最大和最小的量作为初始凝聚点,将n个样本分为2类.设2个初始的凝聚点的集合为

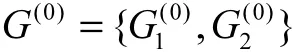
计算新的判别标准值

式中 nl为 G2(0)中的样本数.

将集合2G中的坐标点进行旋转平移以及投射变换后,转化为一平面上的离散点集 ( xi1, xi2) (i=1,2,… ,m ),采用最小二乘法将其拟合为平面圆曲线[10-13],得到所求大底圆半径.平面上圆方程为[14]
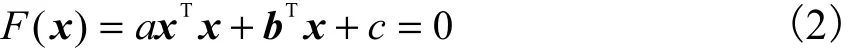
其中 a ≠ 0,x , b ∈R2.通过给定的离散点集 ( xi1, xi2)求解系数a、b和c.将离散点集中的坐标点代入式(2)中,得到线性方程组 B u =0,其中
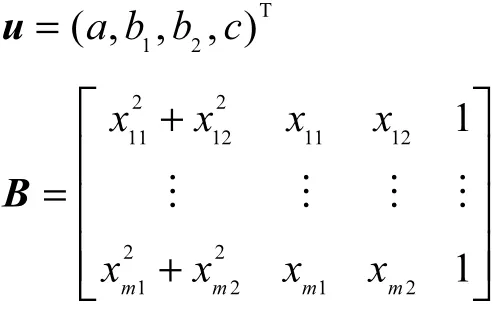
为了得到一个非平凡的解,通常使u2= 1.因为STL模型中数据存在着误差,可转化为
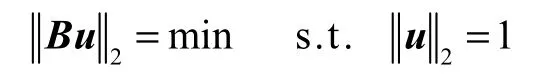
当 0a≠ 时,式(1)变换为
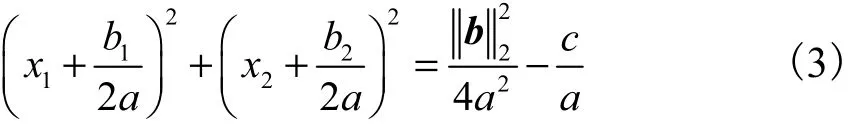
从式(2)中可以得到拟合圆心向量z和半径r,即

当离散点集分布不均匀或者只在部分圆周上分布的情况下,最小二乘法拟合的结果会出现较大的偏差[14-15].设离散点集上各点到圆心的距离方程为

式中 xi=(xi1, xi2).为了使各点到圆的距离的平方和最小,即求解 k =(z1, z2,r )T,使得

将式(3)对k的各个分量进行求偏导数 ∂ ti( k)/∂ki,可得Jacobian矩阵为
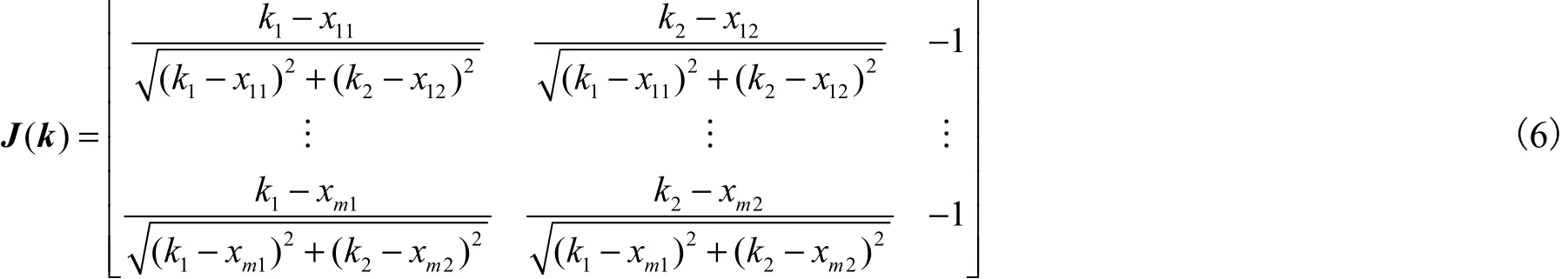
引进向量函数
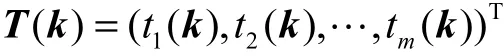
设Gauss-Newton迭代形式为
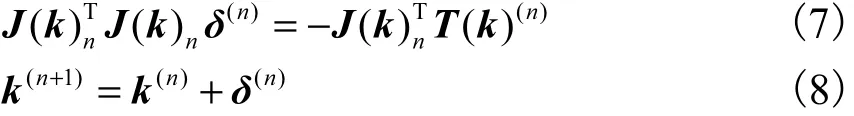
取 δ(n)2=10-6为终止迭代条件,并取离散点集的最小二乘拟合圆的圆心坐标和半径值作为迭代计算的初始向量,迭代求解出圆心坐标和该圆半径.
2.3 圆柱面特征参数的提取
圆柱面特征参数是圆柱面的直径和高度.将圆柱面向垂直于其回转轴线的平面进行投影,得到一个圆或者圆弧,其直径即为圆柱面直径,而圆柱面上各点到该平面带有方向的最大距离和最小距离之差即该圆柱面高度.该投影通过空间坐标变换后,可将 STL模型中记录的圆柱面上的坐标点转化为一平面上的离散点集,利用式(2)~式(8)求解出圆柱面半径1r.
3 旋转面特征参数提取实例
本文所提供的方法已用Visual C++6.0在天津大学自主开发的复杂空间形面制造质量在机检测系统中实现.下面给出由三维CAD生成的STL文件特征数据提取的实例.用 Proe软件做出柱锥相贯的组合体三维模型,保存成 STL格式文件,如图 4(a)所示.根据所读入的STL文件,对几何体中间部位的圆锥面和左侧的圆柱面都给出了正确的几何特征判断,如图 4(b)和图 4(c)所示.并且对这两部分的几何特征参数进行了判定,具体结果如表 1所示.通过实例计算,判别结果的平均精度达到了0.006 27%,完全可以满足工程中实用要求.
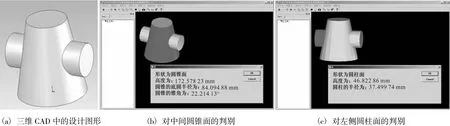
图4 由STL文件提取旋转面几何特征的判别实例Fig.4 Instances of rotational surface characteristic extraction from STL file

表1 几何模型的CAD软件测量数值和判别数值Tab.1 Measured values in CAD and identified values of geometry model
4 结 语
本文提出了从 STL文件中提取出自然二次曲面几何特征及其参数的新方法.该方法利用 STL文件中三角面片法向量在高斯映射图像体现的概率统计规律,并运用快速聚类和Gauss-Newton法相结合,从STL文件中提取自然二次曲面的几何特征并确定其相关数值.通过对CAD软件生成的STL文件进行特征数据提取的实例,验证了该方法的有效性.根据该方法利用 Visual C++6.0开发了相关软件功能,并成功应用于天津大学自主开发的复杂空间形面制造质量在机检测系统中.
[1] 何 荣,李际军. 逆向工程中特征曲面的识别方法[J].计算机应用,2007,27(8):2018-2020.
He Rong,Li Jijun. Feature surface recognition in reverse engineering[J]. Journal of Computer Applications,2007,27(8):2018-2020(in Chinese).
[2] 柯映林,李 岸. 基于主方向高斯映射的旋转面特征提取[J]. 浙江大学学报:工学版,2006,40(6):942-946.
Ke Yinglin,Li An. Rotational surface extraction based on principal direction Gaussian image from point cloud[J].Journal of Zhejiang University:Engineering Science,2006,40(6):942-946(in Chinese).
[3] Stroud J,Xirouchakis P C. STL and extensions[J]. Advance in Engineering Software,2000,31(2):83-95.
[4] 孙玉文,刘 健,刘伟军. 快速成型中 STL数据模型的B-Rep实体精确重建[J]. 计算机辅助设计与图形学学报,2004,16(7):944-949.
Sun Yuwen,Liu Jian,Liu Weijun. Reconstructing accurate boundary representation from STL model[J]. Journal of Computer-Aided Design and Computer Graphics,2004,16(7):944-949(in Chinese).
[5] Horn B K P. Extended Gaussian image[J]. Proceedings of the IEEE,1984,72(12):1671-1686.
[6] Sunil V B,Pande S S. Automatic recognition of features from freeform surface CAD models[J].Computer-Aided Design,2008,40(4):502-517.
[7] Schneider P J,Eberly D H. 计算机图形学几何工具算法详解[M]. 周长发,译. 北京:电子工业出版社,2005.Schneider P J,Eberly D H. Geometric Tools for Computer Graphics[M]. Zhou Changfa Trans. Beijing:Electronics Industry Publishing House,2005(in Chinese).
[8] 单东日,柯映林. 反求工程中点云数据的二次曲面特征提取技术[J]. 计算机辅助设计与图形学学报,2003,15(12):1497-1501.
Shan Dongri,Ke Yinglin. Quadric feature extraction from points cloud in reverse engineering[J]. Journal of Computer-Aided Design and Computer Graphics,2003,15(12):1497-1501(in Chinese).
[9] 向东进. 实用多元统计分析[M]. 武汉:中国地质大学出版社,2005.
Xiang Dongjin. Applied Multivariate Statistical Analysis[M]. Wuhan:China University of Geosciences Press,2005(in Chinese).
[10] Chernov N,Lesort C. Least squares fitting of circles[J].Journal of Mathematical Imaging and Vision,2005,23(3):239-252.
[11] Ahn S J,Rauh W,Warnecke H-J. Least-squares orthogonal distances fitting of circle,sphere,ellipse,hyperbola,and parabola[J]. Pattern Recognition,2001,34(12):2283-2303.
[12] Lukacs G,Martin R,Marshall D. Faithful least-squares fitting of spheres,cylinders,cones and tori for reliable segmentation[J]. Lecture Notes in Computer Science,1998,1406:671-686.
[13] Fitzgibbon A,Pilu M,Fisher R B. Direct least square fitting of ellipses[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,1999,21(5):476-480.
[14] Gander W,Golub G H,Strebel R. Least-squares fitting of circles and ellipses[J]. BIT Numerical Mathematics,1994,34(4):558-578.
[15] 刘元朋,张定华,桂元坤,等. 用带约束的最小二乘法拟合平面圆曲线[J]. 计算机辅助设计与图形学学报,2004,16(10):1382-1385.
Liu Yuanpeng,Zhang Dinghua,Gui Yuankun,et al. Fitting planar circles with constrained least squares[J].Journal of Computer-Aided Design and Computer Graphics,2004,16(10):1382-1385(in Chinese).
