孪生素数问题研究

谭松柏 谭学先

(湖南省益阳市电业局,湖南 益阳 413000)

孪生素数问题研究

谭松柏 谭学先

(湖南省益阳市电业局,湖南 益阳 413000)

大于 3的素数,含在 6n-1、6n+1两数列中。通过对数列序号 n的研究,发现了 6n-1及 6n+1两列数中的合数项所对应序号 n的分布规律——集中分布在模 p数表的两列数中。通过利用模p数表的特性筛去所有合数项所对应序号 n的方法,最终得出了“孪生素数有无限多”以及“大于 8的偶数都可表为二素数之和,且偶数越大,表为二素数和的表法个数就越多。当数值相近时,能被 6整除的偶数,比不能被 6整除的偶数,上述表法个数几乎多,一倍”的结论。

数列;序号;素数;合数;偶数;模 P

一、自然数的分类及素数、偶数的类型与相关名词、符号的定义

现将大于 3的自然数分成 A,B,C,D,E及 F六列算术数列,其通项分别为:(6n-2),(6n-1),(6n),(6n+1),(6n+2),(6n+3),(n=1,2,…m)。对于一个任意大的自然数 X来说,其序号m的精确计算通式为m=[X/6+0.4],适当舍入后可简略为 m=X/6。

以上 A、C、E及 F四列数中,因含因数 2或 3而都为合数,故大于 3的素数,都包含在 B、D两列中,即 6n-1和 6n+1两种类型,以下分别称为Ⅰ型数和Ⅱ型数。其中的素 (合)数项及序号 n的都分别标以Ⅰ、Ⅱ的 下标,并分别称为Ⅰ、Ⅱ型素数、合数、序号等。按 P代表素数、C代表合数的惯例,则有 PI(C I)=6n IP(n IC)-1,PII(C II)=6n IIP(n IIC)+1,其中 PI即为Ⅰ型素数,C II即为Ⅱ型合数…,余类推。

当 6n-1和 6n+1同时为素数时,此二素数即为孪生素数,该序号 n我们称作双重素数序号,记做 np。

二、I、II型合数的因式分解规律

任一 I型或 II型合数作完全的因式 (数)分解,则最终得到的将是一系列的 I、II型素数 (PI和 /或 PII)的乘积。即有:

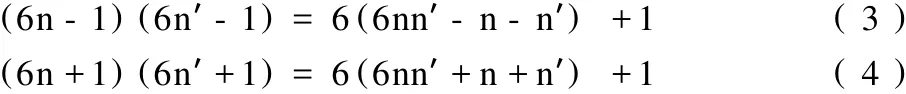
以上可表述为:I型数 ×II型数 =I型数;I型数 ×I型数=II型数;II型数 ×II型数 =II型数。

根据上述 I、II型数的特点并结合 (1)式,我们可得出 C I和C II的因式 (数 )分解规律,即:

三、合数序号 n IC、n IIC的分布规律

四、模数为素数 P的数表 (简称模 P数表)及其特性

1.将通项序号 1,2…m排成列数固定为 P的数表即称为模 P数表,下面表 (一)与表 (二 )分别是 P为 I型素数 5和 II型素数 7的情形:

表 (一) 模 5(PI)数 表表中仅列出模 PI的主要列数据

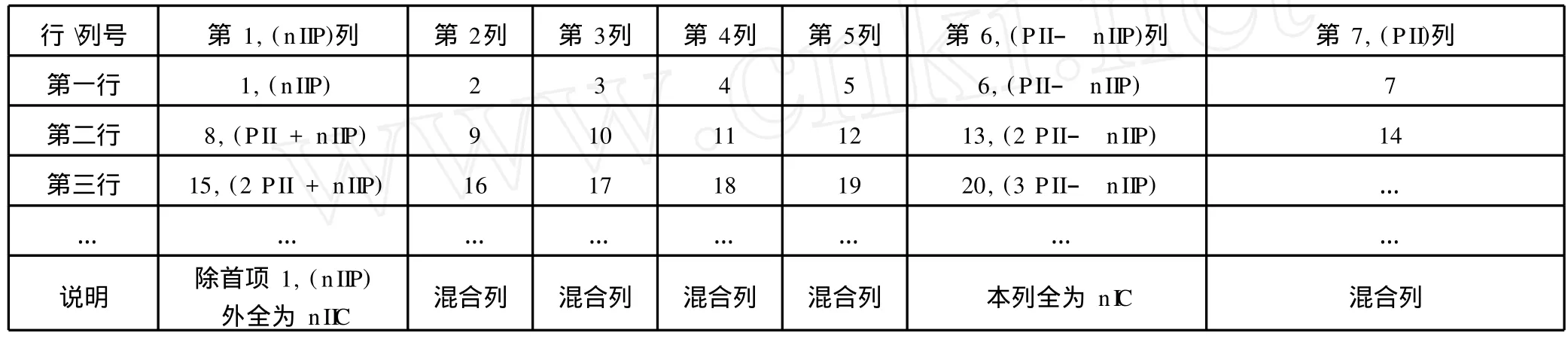
表 (二) 模 7(PII)数 表表中仅列出模 PII的主要列数据

2.模 P数表的性质

据模 P数表的构造及运用《同余定理》、《孙子定理》等数学原理推理,就可得到模 P数表的以下性质:

性质 1 模 P数表的每列数都是模数 P的同 (剩)余类;

性质 2 模 P数表都有两列 (其中一列的首项除外)集中分别分布着含有素因子 P的Ⅰ型与Ⅱ型合数序号 [表 (一)、表 (二)中全列带有底纹者,该性质的根据为式 (9)—(12)];

性质 3模 P′数表中的各列元素,每列都是均匀分布在模P″数表的各列中。此性质简称“均布性质”。

3.模 P数表的应用

要筛掉第 1节 B与 D两列数中所有≯X的合数的序号,就要建立分别由素数 5,7,…到素数 Pk的连续相邻的 k个素数为模的一群数表进行筛选。其中最大素数 Pk的取值范围为Pk 2≯X,或 Pk≯X1/2。

证明如下:

证 设 C=Pk×PX(Pk≤PX),C≯X,,因每个模 P数表都有两列为含素因子 P的合数序号,即 C的序号同时存在于模Pk与模 PX两个数表中,仅需用模 Pk数表即可筛选掉合数 C的序号。因此我们如用上述由 5,7,…,Pk等素数分别为模的数表,就可筛选掉B与 D两列数中所有不大于 X的合数的序号。证毕。

5孪生素数问题

由给定的 X即可得其序号 m=X/6,确定 m后即可确定一个 n=1,2,3,…,m的序号数列。在此数列中首先筛去全部的 n Ic,剩下的就全部是 n Ip;然后再在此数列中筛去一次全部的 n IIc,最后剩下的序号就全部是双重素数序号 np了,而这些剩余序号的数量即就是≯X范围内孪生素数的数量了。

利用模 Pi(5≤Pi≤X1/2;i=1,2,…,k)数表群完成筛选过程。先用模 5数表筛选,即筛去m个序号中的 1/5个Ⅰ型合数序号 (即其中 1列,见数表性质 2),再筛去 m个序号中的 1/5个Ⅱ型合数序号,故经过模 5数表筛选后,剩下了 3列共 m(1-2/5)个序号。依模 P数表性质 3—“均布性质”,这筛剩的3列共 m(1-2/5)个序号,每列都均匀分布在模 7数表的 7列中。即模 7数表的每列中分布有模 5数表筛剩的 m(1-2/5)×1/7个序号,按同样的方式筛去 2列后,即剩下 5列共 m(1-2/5)(1-2/7)个序号。依此继续 .…,故用模 Pi(5≤Pi≤X1/2;i=1,2,…,k)数表群逐个筛完后,即得到了不大于 m的双重素数序号 np,亦即≯X的孪生素数的对数,设其为 R(X)。因每个模 P数表,其中有一列的首个素数序号当作合数序号筛去了,因而使筛剩的素数序号就比实际值要少,故计算所得结果为双重素数序号 np个数的下界,即:

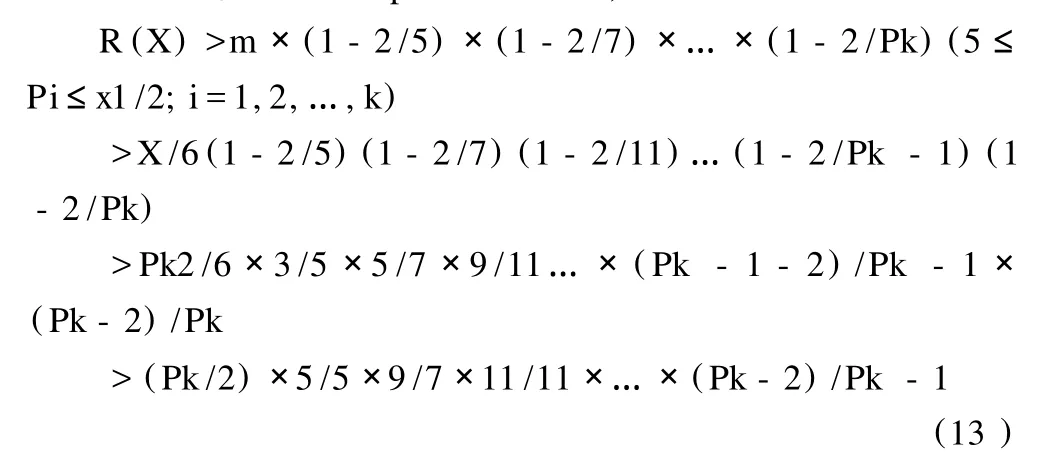
因素数有无限多,故连乘积必随 X的增大而增大,当 X→∞时,R(X)→∞,故得出结论:孪生素数有无限多。

六、哥德巴赫猜想的一点思考

“孪生素数问题”与“哥德巴赫猜想”是相互关联的问题。求“双重素数序号”时,是在 1到 m的序号数列中分别筛去合数序号 n I,与 n II,从而得到 nP。研究“哥德巴赫猜想”,其方法实质上是非常类似的,即:设偶数 E为 6n型偶数,记为 E6,可得到模 Pi(5≤Pi≤E1/2;i=1,2,…,k)数表群;又 E6=(6n′-1)+(6n″+1),因此可得 n′与 n″两列共 n-1对序号 ,每对序号和均等于 n,故称 n′与 n″,互为“配对序号”,即:

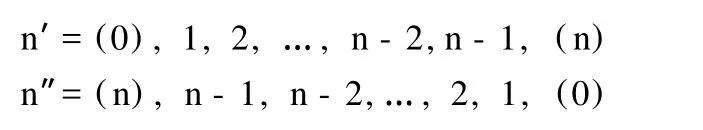
在 n′列中筛去Ⅰ型合数序号,在 n″列中需筛去Ⅱ型合数序号,剩下仍可配对的序号就对应一个哥德巴赫数。按照上述孪生素数的筛选方法,即可得到以下与(13)类似的结果:

设 G(E6)为表偶数 E6为两个素数和的表法个数,则有:

对于 6n-2型偶数,记为 E-2,有:E-2=(6n′-1)+(6n″-1),由于 n′对 n″与 n″对 n′是对称重复的 ,故“表法个数 ”将有不超过一半是重复的,因而有:

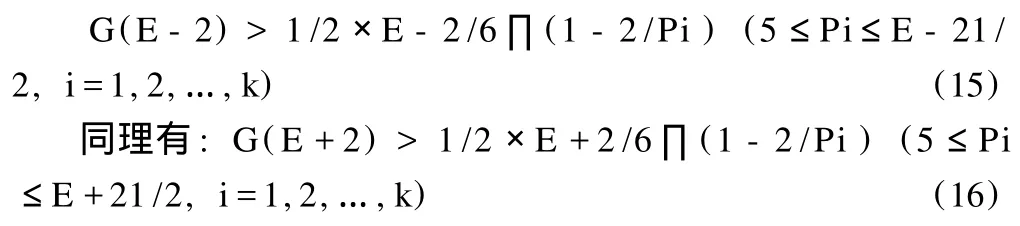
由此可认为凡大于 2的偶数都可表为二素数之和,且偶数越大,表为二素数和的表法个数就越多。当数值相近时,能被6整除的偶数,比不能被 6整除的偶数,上述表法个数几乎多,一倍。

[1] 闵嗣鹤,严士健 .初等数论[M].北京人民教育出版社,1982.

[2] 华罗庚 .数论导引[M].北京科学出版社,1957.

[3] 潘承洞,潘承彪 .哥德巴赫猜想[M].科学出版社,1984.

[4] 熊全淹 .初等整数论[M].湖北教育出版社出版,1982.

[5] 柯召,孙琦 .数论讲义[M].高等教育出版社,2001.

A Research on Tw in Pr im es

TAN Song-bo;TAN Xue-xian
(Hunan Yiyang Electric O ffice,Y iyang 413000,Huan)

Any p rimesbigger than 3 are inc luded in the 2 sequencesof6n-1 and 6n+1.Through a carefulanalysison the seriesnumbern,it is discovered that in the2 sequencesof6n-1 and 6n+1,those nsaccording to the term sare composite numberare concentrated in two sequences of the number list inmodulusp.Through away to sieve outall the nswhich the term sare composite number,it is demonstrated that:“tw in p rim es are unlim ited”and“Any even numberbigger than 8 can be the sum of two p rim esand the bigger the even number,themore the p rimematches,and when the even numbers are in form of6n,the amountof p rimematchesare nearly doublemore thanwhatwhen the even numbersare formed in 6n-2 and 6n+2?”.

sequence,series num ber,p rim e num ber,composite num ber,even num ber,modu lus P

G424

A

1671-5004(2010)06-0152-03

2010-11-05

谭松柏 (1930-),男,湖南益阳电业局高工,研究方向:电气自动化。