高阶多点边值问题共振情况下正解的存在性

刘丙镯, 车晓飞

(中国矿业大学 理学院,江苏 徐州 221116)

高阶多点边值问题共振情况下正解的存在性

刘丙镯, 车晓飞

(中国矿业大学 理学院,江苏 徐州 221116)

针对高阶多点共振边值问题研究较少的情况,利用 Leggett-W illiams型迭合度理论,探讨一类高阶微分方程多点边值问题共振情况下正解的存在性。通过合理的假设,得到了存在正解的充分性条件,并举例说明了结论的可行性。

多点边值问题;Leggett-W illiams型迭合度理论;正解;存在性定理

Abstract:A imed at higher order multi-point boundary value problems at resonance.This paper seeks to probe into the existence of positive solutions fornth-ordermulti-point boundary value problems at resonance,by the method ofLeggett-W illiams norm-type theorem due to D.O’Regan and M.Zima.The paper provides an example to demonstrate the results.

Key words:multi-point boundary value problems;Leggett-W illiams no rm-type theorem;positive solutions;existence theorem

0 引 言

文中主要研究一类高阶微分方程多点边值问题正解的存在性,方程为

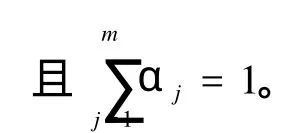
近年来,非局部多点边值问题的研究受到了很多学者的关注[1-7],同时得到了一些多点边值问题存在正解和存在多个正解的充分性条件[8-12]。多数学者研究的是非共振情况下正解的存在性,也就是线性算子 L是可逆的。D.O’Regan和 M.Zima在文献[13]中给出了一种新的研究方法,该方法被G.Infante和M.Zima用于研究共振情况下的二阶多点边值问题[14],方程为对应的边界条件为笔者受文献[14]的启发,用 Leggett-W illiams型的迭合度理论研究了一类高阶微分方程多点边值问题(1)、(2)在共振情况下正解的存在性。

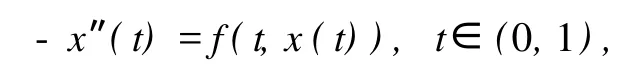
1 预备知识

先介绍一些有关 Fredholm算子和 Banach空间中的锥的知识。令 X、Y是实的 Banach空间,L:domL⊂X→Y是个线性算子,N:X→Y是个非线性算子。假设:

(H1)L是一个指标为零的 Fredholm算子,即I

mL是个闭集并且 dim kerL=co d im ImL<∞。若(H1)成立,则存在连续的投影算子 P:X→X和 Q:Y→Y满足 ImP=kerL,kerQ= ImL[14-15]。因为dim ImQ=dim kerL,所以存在同构 J: ImQ→kerL。用 Lp表示 L定义在 domL∩kerP上,则 Lp是从domL∩kerP到 ImL的一个同态。Kp记为算子 Lp的逆,所以有 Kp: ImL→domL∩kerP[14-16]。显然有抽象方程 Lx=Nx等价于 x=(p+JQN)x+Kp(I-Q)Nx。

定义 2[14]如果 X中凸闭子集 C满足条件

(i)若 x∈C,λ≥0则λx∈C,

(ii)若 x、-x∈C,则 x=0。则称 C是 X的闭锥,

设 C是 X中的闭锥,则有

x≺y当且仅当 y-x∈C。

引理 1[13]如果 C为 X中的一个锥,那么对每一个 u∈C{0}都存在一个正数σ(u)使得‖x+u‖≥σ(u)‖x‖,∀ x∈C。

令γ:X→C是一个压缩映射,即对∀x∈C都有γ(x)=x成立。为了证明的方便,定义

ψ:=P+JQN+Kp(I-Q)N,

ψγ:=ψ°γ。

引理 2[6](Leggett-W illiams型迭合度理论)C为 X中的一个锥,令Ω1、Ω2为 X中的有界开集,并且1⊂Ω2,C∩(2Ω1)≠∅。假设(H1)成立并满足:

(H2)在 X中的任意有界子集上,QN:X→Y连续有界,Kp(I-Q)N:X→Y是紧的;

2 主要结果

定理 1 假设存在常数 R∈(0,∞),函数 f:[0,

所以 y-y1∈ ImL,Y1∩ ImL={0},于是 Y= ImL⊕Y1。注意到 dimY1=1,co dim ImL=1。那么 L是一个指标为零的 Fredholm算子,因此条件 (H1)满足。

定义投影算子 P:X→X和 Q:Y→Y分别为

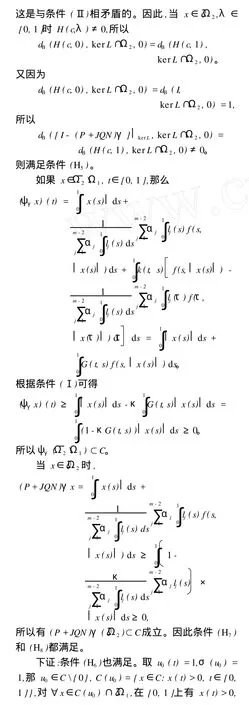
备注 1 条件 (Ⅱ)和 (Ⅲ)不能被用于证明存在多个正解的充分性条件。

备注 2 如果投影算子 Px=x(0),那么定理1中就不能用于验证条件 (H7)和 (H8)了。

下面给出一个例子来说明文中定理可行。

例 1 考虑边值问题 (1)、(2),其中 f(t,x)定义为

[1] L IU YUJI,GE WEIGAO.Solvability of nonlocal boundary value problems for ordinary differential equations of higher order[J].NonlinearAnal,2004,57(3):435-458.

[2] L I U YUJI.Solvabilityof periodic boundary value problems fornthorder ordinary differential equations[J].Appl.Math.Comput,2006,52(6/7):1 165-1 182.

[3] PALAM IDES P K.Multi point boundary value problems at resonance forn-order differential equations:positive and monotone solutions[J].Electron.J.Differential equations,2004,2004(25):1-14.

[4] FENGW,WEBB J R L.Solvability of three-point boundary value problems at resonance[J].NonlinearAnal,1997,30:3 227-3 238.

[5] L I U B.Solvability of multi-point boundary value problem at resonance( IV)[J].Appl.Math.Comput,2003,143(2/3):275-299.

[6] L IU B,ZHAO ZHI L IANG.A note on multi-point boundary value problems[J].NonlinearAnal,2007,67(9):2 680-2 689.

[7] MA R.Multiplicity results for anm-point boundary value problem at resonance[J].Indian J.Math,2005,47(1):15-31.

[8] BA ICHUANZHI,FANGJ INXUAN.Existence ofpositive solutions for three-point boundary value problems at resonance[J].J.Math.Anal.Appl,2004,291(2):538-549.

[9] JIDEHONG,T IAN YU,GEWEIGAO.Positive solutions foronedimensionalp-laplacian boundary value problems with sign changing nonlinearity[J].Nonlinear Anal,2009,71(11):5 406-5 416.

[10] L IANG SI HUA,ZHANG JIHU I,WANG ZHIYONG.The existence ofmultiple positive solutions for multi-point boundary value problems on the half-line[J].J.Math.Anal.Appl,2009,228(1):10-19.

[11] L I GAOSHANG,L IU XIPI NG,J IA MEI.Positive solutions to a type of nonlinear three-point boundary value problem with sign changing nonlinearities[J].Appl.Math.Comput,2009,57(3):348-355.

[12] SUN YONGP ING.Existence of triple positive solutions for a third-order three-point boundary value problem[J].J.Comput.Appl.Math,2008,221(1):194-201.

[13] O’REGAN D,Z IMA M.Leggett-williams norm-type theorems for coincidences[J].Arch.Math,2006,87(3):233-244.

[14] INFANTE G,Z IMA M.Positive solutions ofmulti-point boundary value problems at resonance[J].Nonlinear Anal,2008,69(8):2 458-2 465.

[15] Z IMA M.Fixed point theorem of leggett-williams type and its application[J].J.Math.Anal.Appl,2004,299(1):254-260.

[16] 刘丙镯,车晓飞,陈春香.一类三阶微分方程非局部边值问题的可解性[J].黑龙江科技学院学报,2010,20(3):237-341.

[17] 暴宁伟.一类高阶微分方程边值问题正解的存在性[J].河北工程大学学报:自然科学版,2007,24(2):108-110.

(编辑 王 冬)

Positive solutions ofnth-order multi-point boundary value problems at resonance

L IU B ingzhuo, CHE X iaofei
(College of Sciences,China University ofMining&Technology,Xuzhou 221116,China)

O175.8

A

1671-0118(2010)05-0395-04

2010-05-11

刘丙镯 (1985-),男,山东省济宁人,硕士,研究方向:常微分方程,E-mail:tuteng3839@163.com。