2n阶边值问题正解的存在性与多解性

陈春香

(中国矿业大学 理学院,江苏 徐州 221116)

2n阶边值问题正解的存在性与多解性

陈春香

(中国矿业大学 理学院,江苏 徐州 221116)

为了研究一类非线性 2n阶两点边值问题正解的存在性,通过建立一个特殊锥,利用锥压缩与锥拉伸不动点定理,得到了该问题一个或多个正解存在的充分条件,拓展了已有结果。

边值问题;不动点定理;正解;存在性

Abstract:This paper is an attempt to investigate the existence and multiplicity of positive solutions for 2nth-order boundary value problemswith two points.The construction of special cone and the use of the fixed-point theorem of cone expansion or compression type lead to the sufficient conditionsof the problem,expanding the existing results.

Key words:boundary-value problem;fix-point theorem;positive solution;existence

0 引 言

在自然科学、应用科学等领域,常微分方程边值问题正解的存在性与多解性已经成为一个重要的研究热点,很多学者对其进行了研究[1-10]。其中,文献[3]利用锥压缩与锥拉伸不动点定理讨论了非线性四阶边值问题

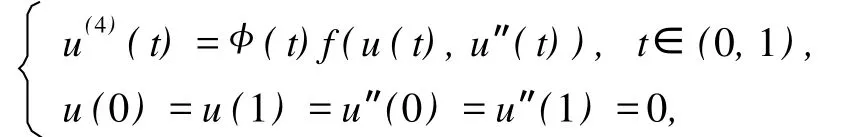
正解与多个正解存在的充分条件。文献[4]利用同一定理讨论了非线性四阶两点积分边值问题

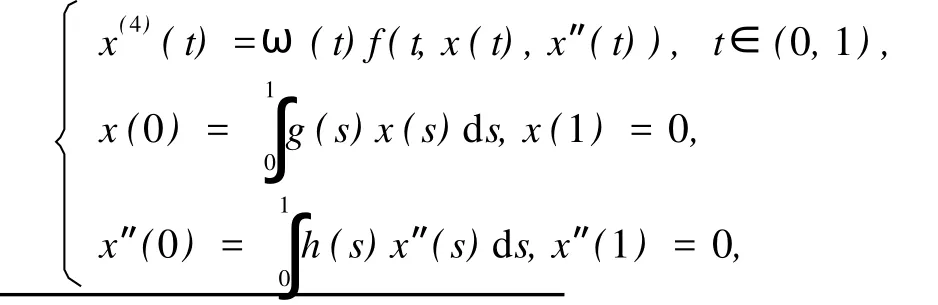
正解与多个正解存在的充分条件以及正解不存在的情况。此外,也有学者讨论了高阶边值问题[5-10]。文献[5]和[8]运用上下解方法分别给出了 2n阶两点边值问题正解存在的充要条件和常微分方程正解存在的充分条件。受文献[3]和[4]的启发,笔者利用锥压缩与锥拉伸不动点定理研究 2n阶边值问题

1 预备知识

为了书写方便,引入下列符号:假设 (H1)成立,由方程 (8)及格林函数的性质知:当x∈C2n-2[0,1]时,Ax∈C2n-2[0,1],由式 (11)知Ax∈C2n-2[0,1],由式 (12)知 Ax∈C2n[0,1]。由式(11)及格林函数的性质得:A:C2n-2[0,1]→C2n[0,1]为连续映射,根据嵌入 C2n[0,1]→C2n-2[0,1]的紧性知:C2n-2[0,1]→C2n-2[0,1]为全连续映射。由式 (12)知 x∈C2n-2[0,1]为边值问题 (1)解的充要条件为:x是 A的不动点。

引理4 假设 (H1)成立,则 A(P)⊂ P且 A:P→P是全连续的。

2 主要结果

定理1 假设 (H1)成立,若 η1f0<1<η2f∞,则问题 (1)至少有一个正解。

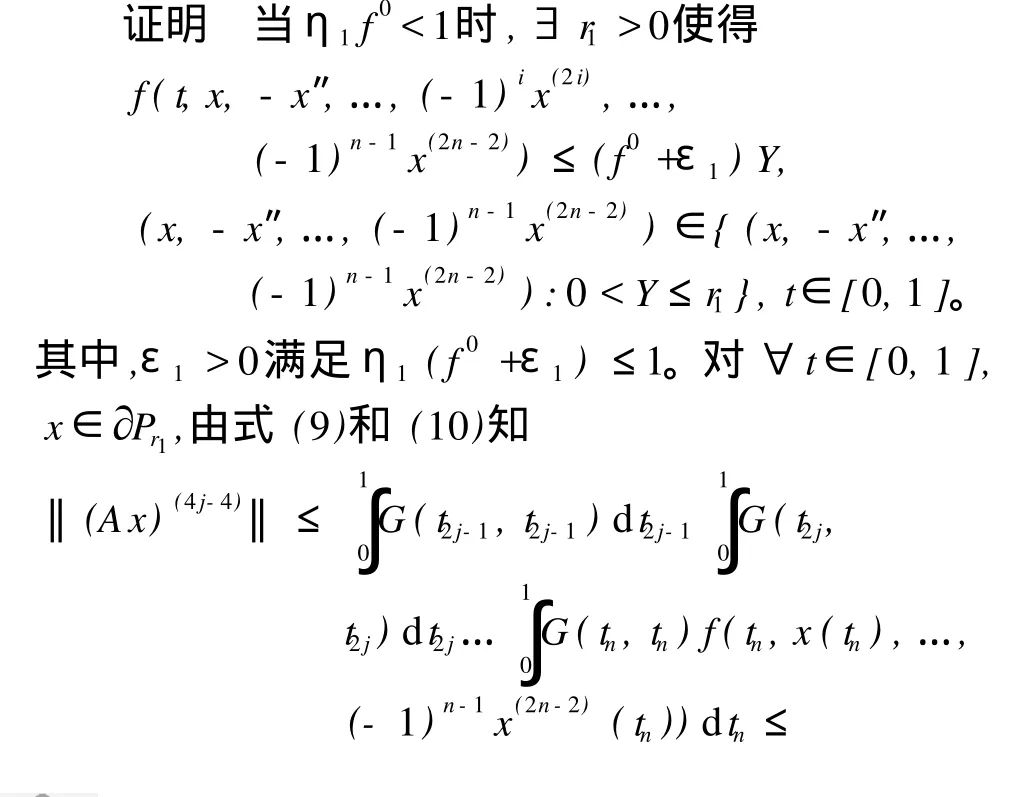
[1] CHEN SHI HUA,N IWEI,WANG CHANGP ING.Positive solution of fourth-order ordinary differential equation with four-point boundary conditions[J].Appl.Math.Lett,2006,19(2):161-168.

[2] ZHANGQ IN,CHEN SHIHUA,LV J INHU.Upper and lower solution method for fourth-order four-point boundary value problems[J].J.Comput.Appl.Math,2006,196(2):387-393.

[3] 李永祥.四阶边值问题正解的存在性与多解性[J].应用数学学报,2003,26(1):109-116.

[4] ZHANG XUEMEI,GEWEIGAO.Positive solutions for a class of boundary-value problems with integral boundary conditions[J].Appl.Math.Comput,2009,58(2):203-215.

[5] WEI ZHONGL I.Existence of positive solutions for 2nth-order singular sublinear boundary value problems[J].J.Math.Anal.Appl,2005,306(2):619-636.

[6] BAI ZHANB ING,GEWEIGAO.Solutionsof 2nth lidstone boundary value problems and dependence on higher order derivatives[J].J.Math.Anal.Appl,2003,279(2):442-450.

[7] CHYAN C J,HENDERSON J.Positive solutions of 2mth-order boundary value problems[J].Appl.Math.Lett,2002,15(6):767-774.

[8] YANG X IAOJ ING.Existence ofpositive solutions for2m-order nonlinear differential systems[J].Nonlinear Anal,2005,61(1/2):77-95.

[9] YAO Q INGL IU.Existence and iteration ofnsymmetric positive solutions for a singular two-point boundary value problem[J].Comput.Math.Appl,2004,47(8/9):1 195-1 200.

[10] L IANG SI HUA,ZHANG JI HU I.Positive solutions of 2nth-order ordinary differential equations with multi-point boundary conditions[J].Appl.Math.Comput,2008,197(1):262-270.

[11] 暴宁伟.奇异一阶微分方程周期边值问题的正解[J].河北工程大学学报:自然科学版,2008,25(2):98-100.

(编辑 王 冬)

Existence and multiplicity of positive solutions for 2nth-order boundary value problem s

CHEN Chunxiang(College of Sciences,China University ofMining&Technology,Xuzhou 221116,China)

O175.8

A

1671-0118(2010)05-0399-04

2010-09-07

陈春香 (1984-),女,江苏省铜山人,硕士,研究方向:常微分方程边值问题,E-mail:chunxiang-chen@sina.com。