改进粒子群算法在PID参数整定中的应用

邵会锋

（通化钢铁股份有限公司氧气厂，吉林通化134003）

1 引言

PID控制器结构简单，对模型误差具有鲁棒性和易于操作等优点，推出半个多世纪以来在各个控制领域中得到了广泛的应用。PID控制器是按偏差的比例（P）、积分（I）和微分（D）通过线性组合构成控制量，对被控对象进行控制。这3个参数整定的好坏不但会影响到控制的质量，而且还会影响到控制器的鲁棒性。因此对PID控制器参数整定的研究成了人们关注的重要问题之一。

随着PID参数整定技术的不断发展，人们提出了各种各样的整定方法。常规的方法一般是基于模型或者基于规则的自整定，随着智能算法的发展，人们提出了一系列的PID自整定方法，如基于模糊规则［1]、基于神经网络［2]以及遗传算法［3]的自整定方法等等。

微粒群优化（Particle Swarm Optimization，PSO）算法具有算法简单易实现的优点，已经被应用于众多工程领域。本文将在原有算法的基础上提出一种改进的微粒群算法，将其应用于PID控制器的参数整定中。该算法克服了传统PID控制器参数寻优的不足，仿真结果表明该算法优于遗传算法的基本微粒群算法。

2 PID控制器描述

PID控制器基本系统原理如图1所示。

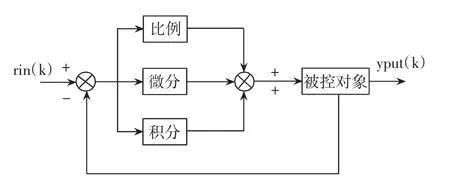
图1 模拟PID控制系统原理框图

PID是一种线性控制器，它根据给定值rin（t）与实际输出值yout（t）构成控制偏差。PID控制器用离散型式的增量控制算式表示为：

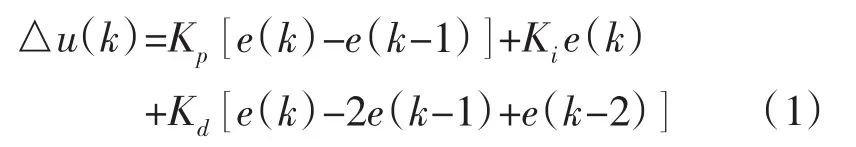
其中：△u（k）是控制器输出地增量，e（k）是控制量偏差，Kp、Ki和Kd分别是比例常数、积分时间常数和微分时间常数。PID控制器的参数优化整定就是要寻找一个合适的Kp、Ki和Kd的组合，平衡控制系统的快速性和稳定性，减少超调，提高系统的响应速度。

3 算法描述

3.1 基本微粒群优化算法

微粒群算法（particle swarm optimization，简称PSO）是Eberhart和Kennedy等人模拟鸟类的捕食行为，于1995年提出的一种新的全局进化优化算法［4]。基本原理是：将优化问题的每个解作用一个粒子，每个粒子在n维空间中以一定的速度飞行，并通过一定的适应度函数来判断粒子位置的优劣，每个粒子根据自身的飞行经验以及群体的飞行经验来调整自己的飞行状态，向空间中的更优位置飞行。粒子自身经过的最优位置称为个体最优值（pBest），整个群体经过的最优位置称为全局极值（gBest）。粒子状态用 D 维速度 vi＝（vi1，vi2，…viD）和位置 pi＝（pi1，pi2，…piD）表示，每个粒子根据下面的公式更新自己的状态，从而产生新一代的群体。

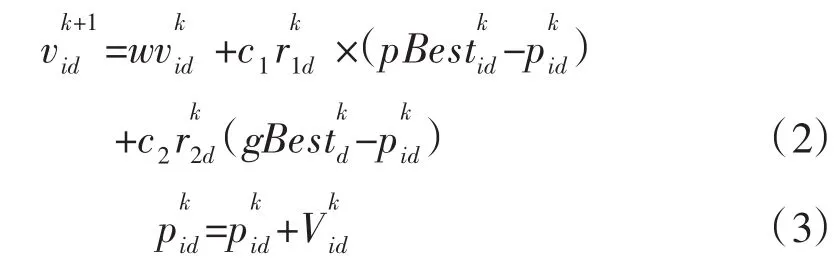
其中：w是惯性权重，c1和c2为加速因子，r1d和r2d是在［0，1] 范围内的两个随机数，k为迭代次数。为了防止粒子远离搜索空间，粒子的每一维速度vd都被限制在［-vdmax，vdmax] 之间。

3.2 改进微粒群优化算法

PSO算法具有概念简单、易于实现、以及较强的全局收敛能力和鲁棒性等优点，但是它同时也具有智能群体算法的固有缺陷，容易陷入局部最优。为了克服粒子群算法的缺点，引入克隆免疫机制构造一种克隆免疫粒子群算法。免疫算法（Immune Algorithm，IA）是受到免疫系统启发而发展起来的一类仿生算法，该算法主要是模拟自然界生物免疫系统的机理和功能而实现的［5]。克隆选择算法是免疫算法中基于克隆选择学说而提出。由于克隆选择算法中存在着选择，克隆以及变异操作可以保证解的多样性。

本文的做法是在粒子群算法外部建立一个规模为初始粒子个数1/10的最优解集m。每当粒子群算法出现一个新的全局最优解gBest，就将其加入到最优解集中,替换最优解集中适应度最小的解，使最优解集中解的数目保持不变。设置一个变异阀值k，当gBest连续k代没有更新时就认为粒子陷入了局部最优，此时进行克隆选择操作。本文中的克隆、变异和选择按照以下定义进行：

定义1：克隆算子，将最优解集m中的每个粒子克隆复制10倍。

定义2：变异算子，对克隆复制后的每个粒子进行柯西变异，柯西密度函数为

其中：t是尺度参数，并且t＞0。经过柯西变异后，粒子 pi变成 p′i，p′i＝pi+ηδk，式中：δk是由柯西方程产生的随机数，η是修正步长。

定义3：选择算子，用经过柯西变异后产生的粒子直接代替当前的所有粒子。

克隆免疫粒子群算法与基本微粒群算法不同的时，它在原有微粒群算法基础上加入了克隆免疫操作。当粒子群算法陷入局部最优时，对外部最优解集中的粒子进行克隆复制、克隆变异和克隆选择操作，提高了粒子的多样性，帮助算法跳出局部最优解，避免早熟收敛，提高了解的精度。

3.3 评价函数的选取

利用PSO算法来优化PID控制器的3个参数Kp、Ki和 Kd，采用实数编码方式，粒子编码串为［Kp、Ki，Kd] 。参数优化的目的是使阶跃响应的控制偏差趋于零，响应速度尽可能快，响应偏差尽可能小。采用误差绝对值时间积分性能指标作为参数选择的最小目标函数，选用下式作为参数选取的最优指标［6]：

其中：e（t）表示系统误差，u（t）为控制器输出，tu为上升时间，w1，w2，w3为权值。

为了避免产生超调，采用惩罚功能，一旦产生超调，将超调作为最优指标的一项，此时最优指标为：

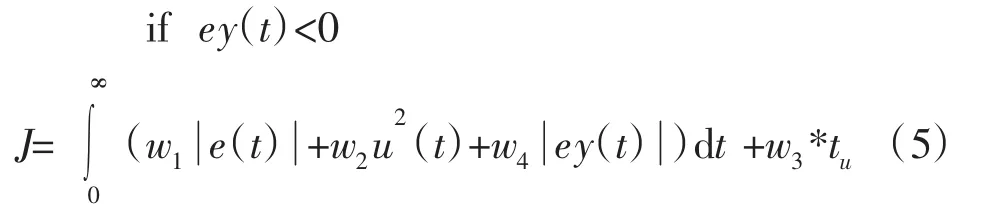
其中：w3为权重，且w4＞＞w1，ey（t）＝yout（t）-yout（t-1），yout（t）为被控对象输出。

3.4 克隆免疫粒子群算法的PID参数优化步骤

应用克隆免疫粒子群算法实现PID控制器参数优化的算法流程如下：

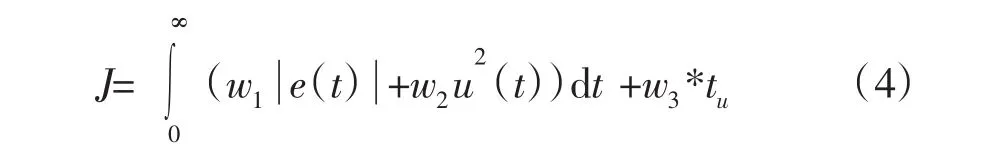
Step1：在规定的搜索空间中随机初始化粒子群位置、速度、历史最优值pBest和全局最优值gBest，并确定 PID 控制器 Kp、Ki和Kd的取值范围；

Step2：按照式（5）计算每个粒子的适应值，并根据适应值更新pBest和gBest以及外部最优解集m；

Step3：判断算法是否陷入局部最优，如果没有，则根据式（1）和式（2）更新粒子速度和位置；否则转式（5）；

Step4：判断是否满足结束条件，满足则输出最优解，结束；否则转Step2；

Step5：对最优解集中的粒子进行克隆免疫操作。

Step5.1：根据克隆算子对最优解集中的每个粒子进行克隆操作；

Step5.2：根据变异算子对克隆后的每个粒子进行变异操作；

Step5.3：根据选择算子对变异后的每个粒子进行选取，更新当前所有粒子；

转Step4。

4 仿真实验

模型的输入信号rin＝1为阶跃信号，采样周期为0.001s。

基于MATLAB6.5进行仿真实验，比较了改进粒子群算法IPSO和基本粒子群算法BPSO以及遗传算法GA在PID控制器线性调节中的表现。算法参数设置：在PID参数优化过程中Kp取值范围为［0，60] ，Ki和 Kd取值范围均为［0，1] 。在 GA 算法中交叉概率pc＝0.9，变异概率pm＝0.033。在BPSO和IPSO中初始粒子种群均为N＝30，进化代数为100代。惯性权重：

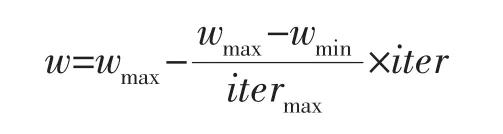
其中：wmax为 0.94，wmin为 0.32，itermax为算法执行的最大迭代次数，iter为当前迭代次数，随着算法的迭代次数增加w动态的减小，有利于加快算法收敛速度。在IPSO算法中变异阀值k＝5，外部最优解集规模为 3。评价函数的参数 w1＝0.999，w2＝0.001，w3＝2.0，w4＝100。经过 100 此迭代，图 2 所示为三种不同算法优化PID参数的评价函数值收敛趋势图，图3所示为参数整定后系统单位阶跃响应的比较图，表1所示为三种方法参数整定和评价函数的最终结果。

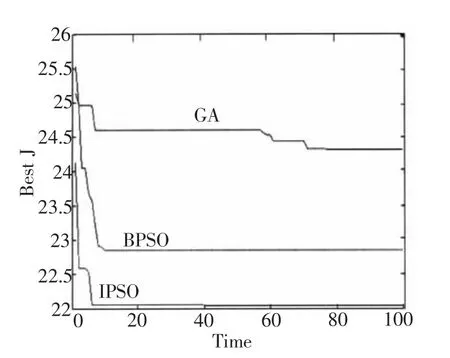
图2 三种算法优化PID参数的收敛曲线图

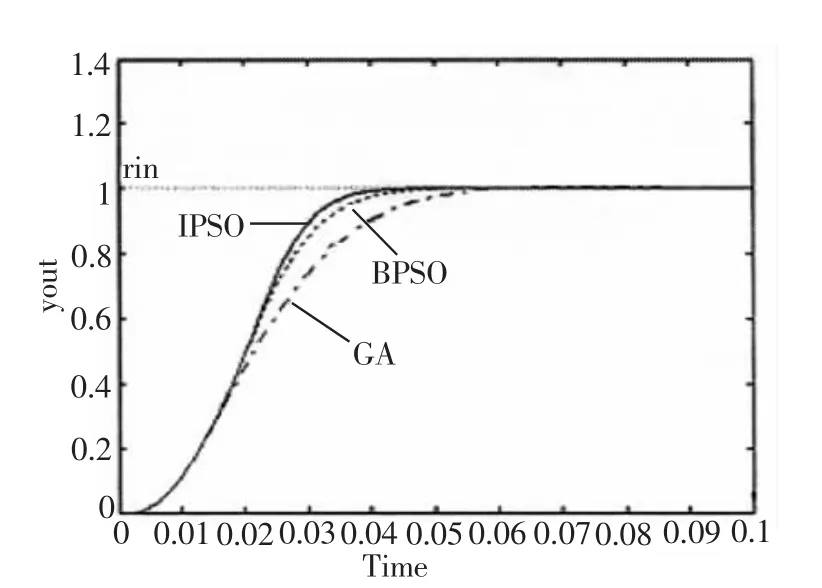
图3 三种算法阶跃响应曲线图

表1 三种算法PID参数整定结果比较

从图2、图3以及表1可以看出：收敛速度、搜索能力以及在系统响应时间上改进的微粒群算法都要优于基本微粒群算法和遗传算法。

5 结论

本文基于克隆选择算子提出了一种改进的粒子群算法，其收敛速度和精度都优于遗传算法和基本微粒群算法，并有效避免了算法容易陷入局部最优的缺点。将其应用于PID参数整定，通过仿真实验证明了算法的可行性和有效性。

［1] Linc,Xu J X，Hang C C.Comparison Between a Fuzzy PID Controller and a Kind of Nonlinear PID Controller［C] .Proc 36th IEEE Int Conf On Decision and Control S Diego（CA）,1997.

［2] 张世峰，李鹏.基于神经网络的自整定PID参数控制器设计［J] .自动化仪表，2009，30（7）：64-66.

［3] 周志，干树川.基于遗传算法的控制参数优化研究［J] .计算机应用，2007，27：191-192.

［4] Kennedy J,Eberhart RC.Particie Swarm Optimization［C] .In:Proc.of the IEEE Int’1 Conf on Neural Networks.Perth:IEEE Inc，1995:1942-1948.

［5] Dasgupta D.Artificial Immune System and Their Applications［M] .Springer-Verlag，1999.

［6] 刘金琨.先进PID控制MATLAB仿真［M] .第2版.北京：电子工业出版社，2004:223-228.