基于神经网络辨识的模糊预测函数控制

周祥龙，赵景波

（1.青岛海军潜艇学院，山东青岛266071；2.青岛理工大学，山东青岛266071）

1 前言

工业锅炉是工业生产中普遍使用的动力设备，是能源转换的重要设备之一。工业锅炉的燃烧控制直接与节能有关，因而是锅炉控制系统的关键，对安全经济运行具有十分重要的意义。

预测函数控制（Predictive Functional Control简称PFC）方法是基于预测控制原理控制研究中发展起来的一种新型的预测控制算法［1]。该控制方法具有算法简单、计算量小、跟踪快速等特点。单纯采用预测模型进行过程输出值的预测只是一种理想的方式，因为实际过程中存在非线性、时变以及干扰等因素，基于预测模型得到的输出预测值不可能与实际完全相符,当模型失配严重时，甚至可能从根本上破坏控制的稳定性。为了更好地提高预测函数控制的鲁棒性，本文尝试用模糊推理的方式对误差进行补偿，即控制量为预测函数控制量与模糊补偿量之和，其控制结构如图1所示。并把该算法应用于锅炉燃烧控制系统设计中，通过仿真，说明该算法是有效的。

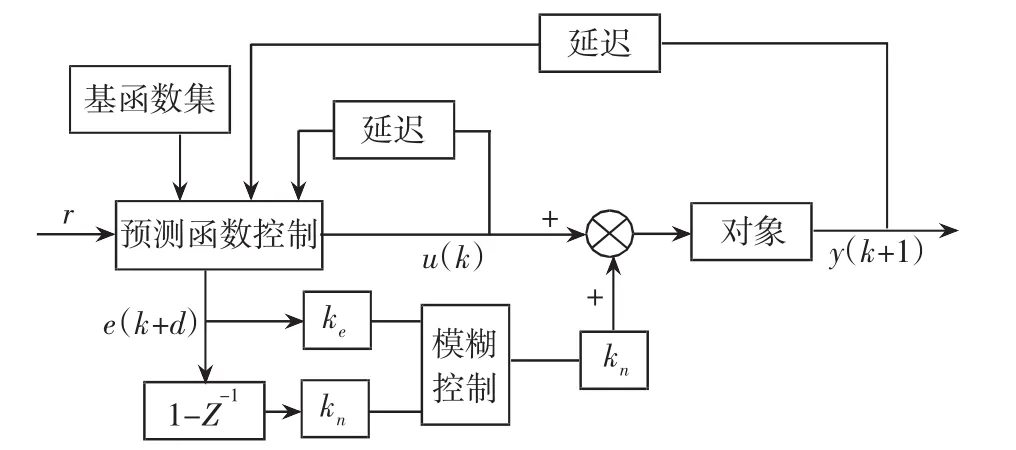
图1 模糊补偿的预测函数控制

2 工业锅炉燃烧系统及其控制

工业锅炉的燃烧过程是一个具有强干扰的非线性、时变多变量过程，可以分为蒸汽压力、烟气含氧量及炉膛负压3个回路。

蒸汽压力通常要求稳定在一个设定值附近，所以选择汽压为被控量，控制量是控制链条速度的滑差电机转速，为克服负荷变化对蒸汽压力的影响，引入平均蒸汽流量作为前馈信号。由于在燃烧过程中，受煤质的影响，因此时延较大且有时变，为此，适当选取了控制间隔等项。

送风与引风对于锅炉的燃烧是至关重要的。送风、引风与给煤配合很好，才能达到最佳燃烧和提高锅炉热效率的目的。送风回路以烟气含氧量作被控量，送风挡板开度作控制量。引风回路以炉膛负压作被控量，引风挡板开度为控制量。为克服给煤量的变化对烟气含氧量的影响，引入蒸汽压力控制量作为送风通道的前馈信号。为使煤能够安全燃烧，要求烟气含氧量与负压保持在一个适当值附近，通常要求含氧量较低，负压为微负压。

链条炉燃烧系统是一个复杂的3输入、3输出对象，输出量有：锅炉出口蒸汽压力PM、烟气含氧量O2%、炉膛负压ST；输入量有：给煤量M、送风量V、引风量S，而且各量之间存在着关联。对实际对象进行深入研究后不难发现：炉膛负压主要受送风和引风的影响，而其它各量对它的影响都很小，因而可以把炉膛负压作为带送风前馈的单回路控制系统处理。这样，链条炉燃烧系统就简化为2×2对象，如图2所示。

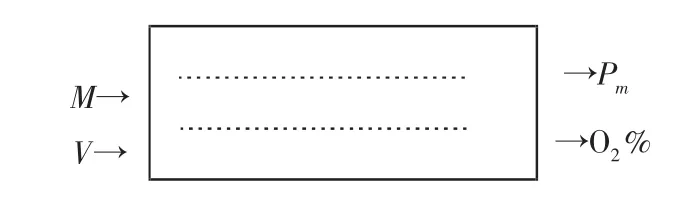
图2 简化后燃烧对象的输入输出关系

3 预测函数控制

预测函数控制（PFC）是基于预测控制原理发展起来的一种新的预测控制技术，具有一般预测控制的三大特点：预测模型、滚动优化、反馈校正，而它与其他预测控制算法的最大区别是注重控制量的结构形式，认为控制量与一组相应于过程特性和跟踪设定值的函数有关。因此每一时刻计算的控制量等于一组事先选定的函数线性组合而成，这些函数称为基函数。用这些基函数的已知过程响应，通过对目标函数进行优化计算得到各基函数的权系数而求出相应的控制量。

为了算法实现的方便，PFC的预测过程模型采用离散状态方程形式的参数模型。其离散状态方程描述为：

控制量被当作是基函数的线性组合，基函数的选择与过程的特性和跟踪设定值有关。通常可取为阶跃、斜坡、抛物线等函数。

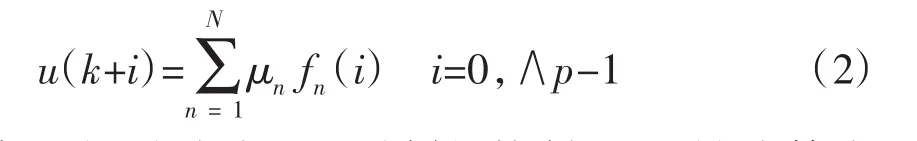
式中：u（k+i）为在 k+i时刻的控制量；fn（i）为第个采样周期时基函数的取值；N为基函数的个数；P为预测优化时域长度；μn为线性组合系数，需优化计算。

为防止出现控制量剧烈变化和超调等现象，需引入一条在预测时域内的指数曲线作为参考轨迹：

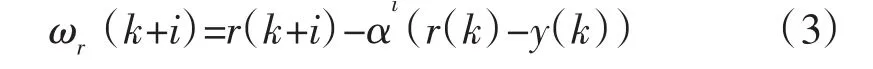
式中：ωr（k+i）为k+i时刻的参考轨迹值；（rk+i）为k+i时刻的设定跟踪值；y（k）为k时刻的被控对象输出测量值 ，0＜α＜1；TS为采样周期；T 为闭环响应时间。

预测k+i时刻的过程输出为：

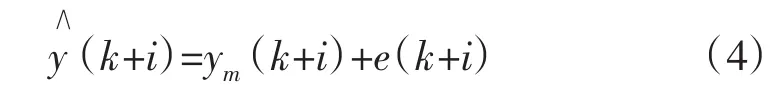
式中：ym（k+i）为预测模型输出；e（k+i）表示过程与模型的预测误差。

预测函数控制的优化目标函数是使得在选定的预测时域H的拟合点上（个数为S）预测过程输出与参考轨迹值差值的平方和最小。

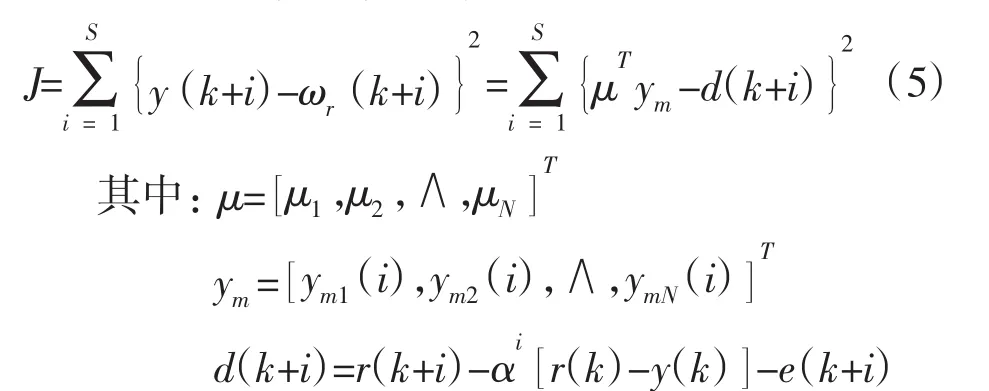
拟合点是介于0-T之间的一些离散点，需预先确定，其个数应大于等于基函数的个数。

极小化性能指标J得系数μ，即

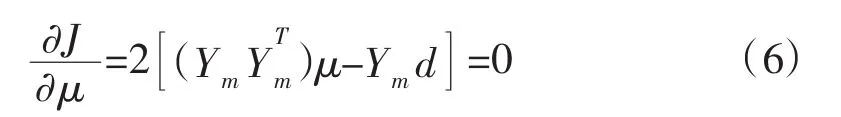
其中Ym是一个矩阵，其列为ym，即

4 模糊补偿

设 e（k）和 ec（k）为 k 采样时刻过程输出的偏差和偏差变化率，过程存在d步纯时延，则模糊补偿控制量由 e（k+d）和 ec（k+d）确定。e（k+d）和 ec（k+d）可由预测模型式（4）和参考轨迹ωr算出。定义 e（k+d）和 ec（k+d）如下：

两个输入模糊变量和输出控制补偿量△u的隶属函数形状均为三角形，如图3所示。采用不均匀分布有助于提高系统的控制精度，共有7个模糊子集：PB，PM，PS，ZE，NS，NM，NB。模糊规则制定的根据是：如果k+d时刻e为正大，且ec也为正大，说明误差有进一步增大的趋势，那么可以推断k时刻过程的输入太小，应增大k时刻控制器的输出，故△u为正大；e同样为正大，若ec为零，说明误差变化趋势不变，控制量可以减小一些，故△u为正中；若ec为负大，说明误差有减小的趋势，控制量可以降到最小，故△u为正小。相反，如果k+d时刻e为负大，且ec也为负大，那么可以推断k时刻过程的输入太大，应减小k时刻控制器的输出，故△u为负大。用同样的分析方法可以得到其它条件下控制量的模糊校正规则，共制定了50条规则。通过重心法解模糊可求出△u，将本部分求出的模糊补偿控制量与预测函数控制量相加即为过程输入控制量。

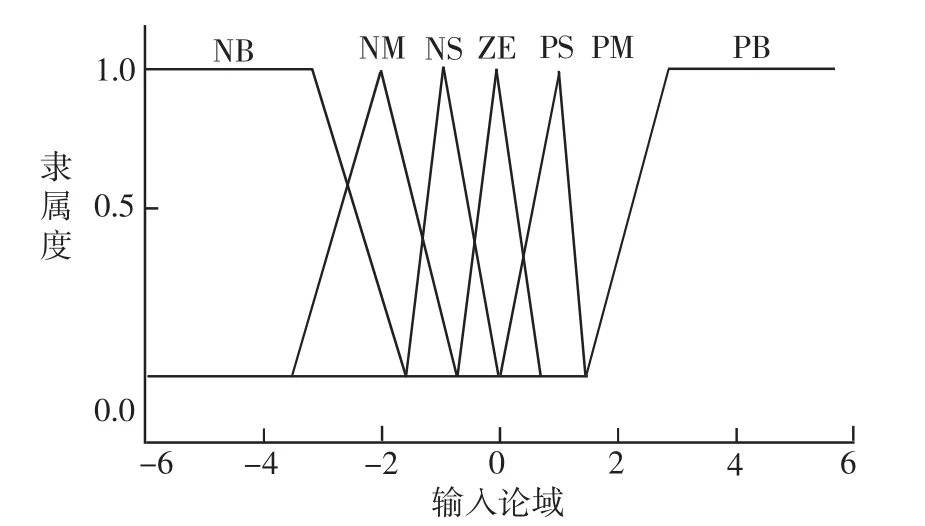
图3 模糊变量隶属函数

5 基于神经网络辨识的模糊补偿的预测函数控制器实现

5.1 参数辨识——基于神经网络递推时变遗忘因子的最小二乘法

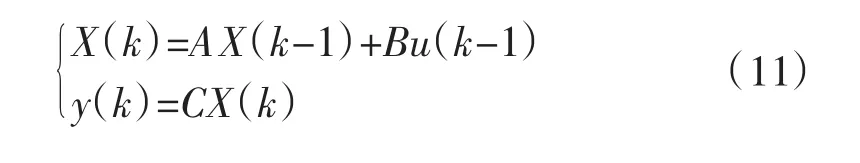
给出预测模型：模型中的多项式A、B与C的阶次根据实际情况而定，它们的系数是通过参数辨识得到的，辨识方法采用基于神经网络递推时变遗忘因子的最小二乘法。神经网络采用扩展Elman神经网络，结构图如图4所示。

图4 扩展Elman神经网络结构图

采用带遗忘因子的阻尼最小二乘算法修改网络权值。

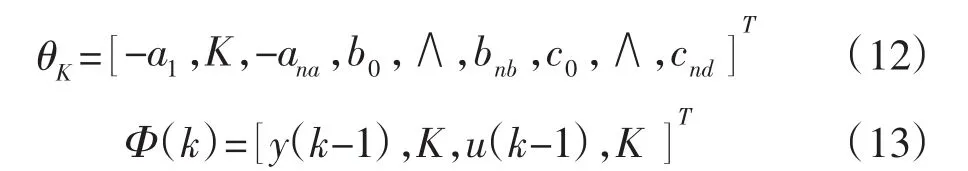
递推算法：

参数σ（k）与C的选择如下：

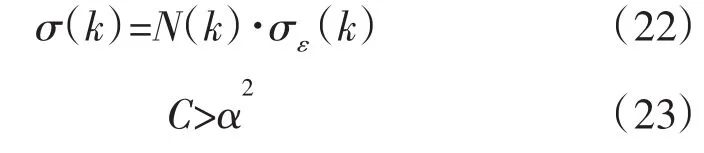
5.2 基于神经网络辨识的模糊补偿预测函数控制的实现

采用基于神经网络递推时变遗忘因子λ（k）的最小二乘法，在线递推辨识参数，能够保证辨识参数既能适应系统的缓慢变化，又不会发生爆发现象。每个采样间隔完成一次递推参数辨识，得到估计模型（11），根据该估计模型，可以得到基于模糊补偿的预测函数控制器的控制信号u（k），并将此次算出的控制量作为被控过程的输入，必然产生与之相对应的输出，然后再进行采样输入输出数据辨识参数。

6 锅炉燃烧系统连续系统仿真

仿真利用 CSS（Continuous System Simulation）的方法，它是一种基于信号流图的系统仿真方法，它把模拟计算机模块化编程结构的思想纳入到数字控制系统仿真的编程中来，具有实时性能好、精度高等特点。

本文基于20t/h链条炉燃烧对象的数学模型（如图5所示）进行仿真，所有控制和仿真软件在IBM—PC机上用C语言编制完成的。辨识采用基于神经网络的时变遗忘因子的最小二乘法。

图5 20t/h链条炉燃烧对象的数学模型

仿真结果：

当蒸汽流量D不变时，Pm、O2%跟踪其给定值阶跃变化的控制过程曲线如图6所示。

图6中曲线①表示Pm跟踪给定值阶跃变化曲线；曲线②表示O2%跟踪给定值阶跃变化曲线。

当Pm、O2%给定值不变，蒸汽流量D作10%阶跃变化时，Pm、O2%跟踪控制过程曲线如图7所示。

图7中曲线①表示蒸汽流量D阶跃变化时的Pm；曲线②表示蒸汽流量D阶跃变化时的O2%。

图6 Pm、O2%跟踪给定值阶跃变化曲线

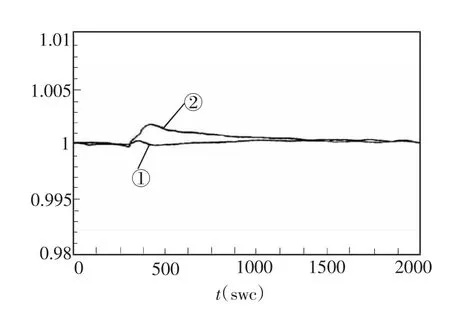
图7 蒸汽流量D阶跃变化时的Pm和O2%

7 结论

本文所提出的工业锅炉燃烧过程的基于神经网络辨识的模糊补偿的预测函数控制，通过仿真实验表明，它是有效的，可行的，具有较强的的适应性和鲁棒性，具有较高的控制精度，并且适应调整参数能使控制动作在保证输出精度之下更加平滑，有利于对现场执行机构的保护，易于整定，因而这种控制器非常适用于工业现场。

［1] Richalet，J.Industrial Application of Model Based Predictive Control［J] .Autotalica，1993，29：1251-1274.

［2] 席裕庚.预测控制［M] .北京：国防工业出版社，1993.

［3] 刘志东，景 旭.控制系统CAD概论［M] .黑龙江科学技术出版社，1995.

［4] 李 翔，陈增强，袁著祉.非最小相非线性系统的简单递归神经网络控制［J] .控制理论与应用，2001，18（3）：456－460.

［5] 林茂琼，陈增强，袁著祉.基于阻尼最小二乘法的神经网络预测偏差补偿自校正控制器［J] .信息与控制，2000，29（1）：27－33.