空气动力作用对高速受电弓受流特性影响研究
2010-09-21宋洪磊吴俊勇郑积浩郑琼林
宋洪磊,吴俊勇,吴 燕,郑积浩,郑琼林
0 引言
随着高速铁路的迅速发展,舒适安全快速的优点已经被越来越多的人所重视,当列车速度达到250 km/h及以上时,高速气流产生的空气动力对列车部件的影响也越来越大,并且空气阻力占到了总阻力的 75%~80%,它影响到高速铁路中受电弓-接触网的受流质量,受流质量的好坏直接影响到列车的行进速度。电能通过接触网悬挂系统经由安装在机车顶部的受电弓传到机车上,而良好的受电弓空气动力性能是保证弓网系统具有良好稳定性和跟随性的重要因素,且空气动力也影响到列车的运行性能,安全运行以及噪声污染等问题。良好的受流应该具有良好的空气动力性能,但这受试验条件限制,因此用计算机仿真成为研究该类问题的一种快捷有效的措施,并且通过数值仿真也有助于新系统的开发和性能要求的提高。
文献[1,4]介绍了弓网系统在高速运行时的受流稳定性分析及影响因素,随着铁道运输高速化,空气动力学现象变得越来越突出[2,3,10],目前开展高速列车空气动力学性能研究有2种典型的方法:一种是实验研究方法,包括实车试验和模型模拟试验[8,11,12],模型模拟试验又包括风洞、水洞、动模型试验;另一种是数值计算[5-7,9]。
本文利用 STAR-CCM+建立了流体力学的仿真模型,通过施加边界来模拟真实环境下受电弓的空气动力性能,采用紊流模型对受电弓在开放空间的空气动力学性能进行分析,研究了风阻对弓网接触压力变化的影响,受电弓受风压的影响情况,为进一步提高弓网动态受流性能及改善气动噪声提供了仿真手段和理论研究基础。
1 受电弓的空气动力学研究
高速列车是在充满着以空气为介质的空间里运行的,其研究对象可以归纳为研究空气流体及在空气流体中的刚体间相互作用的问题,于是引入了流体力学理论。
1.1 研究的流体力学理论
在空气动力学研究中,忽略流体的分子结构,将流体看作是连续介质,其中没有真空的地方,没有分子间隙和分子运动,物质连续地分布于其所占的整个空间,物质宏观运动的物理参数是空间及时间的可微连续函数。该假设对空气动力是成立的,称之为连续性假设或流体介质密度稠度性假设。采用流体连续介质假设后,表征流体属性的物理量为空间和时间的连续函数。由于流体的连续性使得能够把流体的运动学上的各个基本量(如速度、压力等)看作是某些物理量(如时间、空间坐标)的连续函数,这样就可以建立在连续函数基础上的数学模型求解空气动力学问题。
高速列车周围的流场是紊流场即湍流场,湍流是空间中不规则和时间上无秩序的一种高度复杂的非线性流体运动。在湍流中流体的各个物理参数,如压力、温度、速度等都随时间与空间发生随机变化,本文中使用到非线性剪切压力传输(SST)k-ω湍流模型。
SST (k-ω)模型和标准(k-ω)模型相似,但有些改进,该改进使得SST(k-ω)模型比标准(k-ω)模型在广泛的流动领域中有更高的精度和可信度。
SST (k-ω)流动方程如下式:

式中,Gk为由层流速度梯度而产生的湍流动能;Gω为由ω方程产生的;Γk,Γω分别代表k与ω的有效扩散项;Yk,Yω分别代表k与ω的发散项;Dω为正交发散项;Sk,Sω为用户自定义。
下式说明空气的阻力系数和抬升力系数:

式中,cx为空气阻力系数;cy为抬升力系数,Px为受到的空气阻力;Py为受电弓的抬升力。
1.2 受电弓的气动特性
受电弓运行时阻力和气动抬升力与空气流动速度有关。通过研究空气的气动力特性,分析列车在高速运行时,受电弓受到的阻力和框架受到的抬升力,以便于在后期的设计过程中进行优化。
1.2.1 受电弓的阻力
对于受电弓弓头,上臂和下臂进行x,z方向上的气动力分析,再对整个受电弓进行受力分析。根据列车空气动力学的定义,在通常研究中,定义空气动力系数为

式中,Px为受电弓受到的阻力。
1.2.2 受电弓的抬升力
对受电弓的抬升力的研究目的是为了维持弓头平衡,特别是在高速运行情况下,受电弓弓头的平衡稳定运行是良好受流质量的保证。如果弓网接触压力降低到0会造成离线和火花,如果接触压力太高,接触线的抬升量会超过范围,甚至会引起断线等事故。接触网和滑板的磨损也是与接触压力有关系的,为了避免抬升量过高以及过度磨损,要求接触压力不能太大,但是为了避免离线和火花,要求接触压力又不能太小。保证接触线和滑板磨耗最小又不致使导线产生危险的偏离是可靠经济的受流条件。
2 CFD(计算流体力学)数值模拟
2.1 模型的建立和网格的划分
利用三维建模软件UG建立受电弓几何模型,建模过程中需要确定的参数有受电弓上框架、下框架、滑板和弓头的几何参数,通过简化得到的该模型可以在 STAR-CCM+中进行几何体的包面和网格划分。整个计算域为一个长方体,从入口到出口约为受电弓8倍的长度,侧面到受电弓的外侧约为1.5倍的弓宽,顶部到弓顶约为2.5倍的弓高。
确定好模型的计算域,如图1所示,由于受电弓是沿几何X轴对称,故可以只取当前计算域的一半来模拟,以节省计算资源。进行网格参数的设置,由于受电弓各部件的空气动力特性随运行速度变化而不同,所以在弓头和下臂杆部位设定体网格的加密,最后设置网格参数,生成多面体的体网格,该算例中体网格数目为588 605个,这样既可保证网格的质量和求解的高效率,又能提高仿真结果的准确度。

图1 受电弓的计算域及部分表面网格图
2.2 边界条件的设置
计算边界条件的设定如表1所示。

表1 计算边界条件的设定表
2.3 求解器相关参数的设置
该模型选择的是稳态不可压缩流动,k-Omega SST(k-ω)模型和All Y+壁面处理方式。采用Segregated求解器,利用模型的二阶精度计算,设置迭代步数为800步。
3 仿真计算结果及分析
通过对受电弓的数值仿真计算,可以得到受电弓表面风压、速度分布图及阻力和抬升力的变化。
图2是整个受电弓表面受到的风压分布云图。从图中可以看出,在受电弓的弓头和上臂杆与下臂杆连接处受到的压力较大,约为4 000 Pa,因此这是设计中需要重点分析的重要区域。

图2 受电弓表面风压分布云图
图 3是受电弓弓头和平衡杆的侧面方向表面压力云图。图中弓头和平衡杆右方的区域为迎风压力流动滞止面,所以弓头方向受到的压力较大,在弓头下方的平衡杆处的压力也很大,上臂杆和下臂杆连接处也是重点受力区域。正面的风压决定了滑板的正面阻力。

图3 弓头的风压分布云图
图 3中还显示了在迎风方向受到的力明显大于背风侧,因此弓头是分析受电弓在高速空气动力作用的一个重要因素,特别是弓头的稳定作用决定了空气动力的中心,在弓角及平衡杆上安装导流板可以调节压力中心,改善空气动力学性能。由于高速空气的作用,涡流效应会影响背风侧的压力分布,仿真可以显示受电弓各部件在高速空气动力作用下所受的压力情况。
图4是从受电弓的侧面得到的表面速度云图。在弓头的2个滑板处的速度是不一样的,这是由于边界层的分离现象,在分离区中倒流往往形成气流涡旋,使得前滑板的速度要比后滑板速度大些。在上、下臂杆连接处的速度也是明显差别的。杆件前方来流的速度是由于涡旋作用导致的增大,但在后方会使速度减小些。

图4 受电弓的表面速度云图
接下来对受电弓在高速运行中受到的阻力以及抬升力的情况进行分析,首先对受电弓的外流场进行模拟,根据仿真计算结果可以得到受电弓在高速运行时受到的阻力系数。如图5显示的是阻力系数在程序迭代运行过程中的变化情况,在迭代次数达到800步左右时趋于稳定,阻力系数维持在0.75。

图5 阻力系数曲线仿真图
图6显示的是受电弓阻力的变化,对于整个受电弓(没有绝缘子和底座)而言,在速度为350 km/h时,受到的阻力为1 200 N。据文献[13]可知,受电弓气动阻力占列车运行总气动阻力的 8%~14%,可见,应用STAR-CCM+对受电弓的空气动力学性能进行仿真是可行的。

图6 受电弓阻力曲线图
经过 800步迭代受电弓在运行过程中受到的抬升力将趋于125 N,如图7所示。
由经验公式知,平均接触压力Fm= 0.000 97v2+70,动态接触压力标准差σ≤0.3Fm;最大接触压力Fmax=Fm+ 3σ,最小接触力Fmin=Fm- 3σ。当速度为v= 350 km/h时,Fm= 188.825 N,可知空气对于受电弓的抬升力维持在118.825 N左右,由仿真结果推知,受电弓在闭口方向运行时,受到的抬升力125 N左右,在经验公式的范围之内,由此得知,仿真结果基本正确,所以可以通过对受电弓空气动力学性能进行仿真,研究高速下风阻对弓网之间接触力、受电弓弓头和杆件的影响情况,得到受电弓的整体阻力和抬升力,分析出其主要的影响因素,提出合理的解决方案使其控制在合理的范围内,保证受电弓与接触网间良好受流性能。
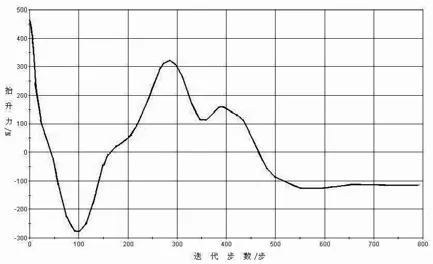
图7 受电弓抬升力曲线图
4 结论
通过分析与研究,得出以下结论:
(1)利用流体力学计算软件 STAR-CCM+进行数值仿真,用UG建立受电弓的三维模型,在合理的边界条件下对受电弓的空气动力特性进行了分析,能够正确地反映弓网的动态受流性能,为进一步研究弓网配合、参数优化提供了有效的手段。
(2)良好的受流性能需要对受电弓的空气动力性能进行设计,因此有必要对受电弓的结构进行优化。
(3)当列车在高速运行时,受电弓上臂和弓头部分处于较高气流的作用下,所以设计出合理形状和安装角度的导流板,安装在受电弓上框架横梁和弓头托架上,通过导流板自身产生的升力来改变受电弓的升力大小,从而改善受电弓高速运行时的空气动力学性能,满足最佳弓网受流要求。
[1]于万聚.高速接触网的受流稳定性分析[J].西铁科技,1996,(2):38-44.
[2]A Collina, A.Facchinetti, and F.Resta, “A feasibility study of an aerodynamic control for a high speed pantograph,” IEEE international conference on advanced intelligent mechatronics,pp.1-6, September 2007.
[3]M.Bocciolone, F.Resta, D.Rocchi, A.Tosi and A.Collina,“Pantograph aerodynamic effects on the pantograph-centenary interaction,” IEEE Vehicle System Dynamic, Vol.44, pp.560-570, 2006.
[4]戴南山.高速受流性能探讨[J].电力机车技术,2001,24(1):17-18.
[5]王一伟,王洋,安亦然,等.基于 LBM 方法的高速列车空气动力学计算[J].中国科学,2008,38(1):1795-1804.
[6]Keen, P.M.; Phillpotts, R.E.; Conway, S, “An instrumented pantograph for high speed current collection measurements,”IEEE international conference on railway condition monitoring, pp.68-73, June 2008.
[7]Joseph A Schetz.Aerodynamics of High-speed trains, Vol.33, No.3, China: Advance in Mechanics, 2003, pp.404-423.
[8]田红旗.风环境下的列车空气阻力特性研究[J].中国铁道科学,2008,29(5):108-112.
[9]李人宪,刘应清.高速列车紊态外流场的数值模拟研究[J].应用力学学报,2001,18(1):6-13.
[10]姚林强,陈燕荣.高速列车空气动力学综合性能研究[J].四机科技,2004,4:4-6.
[11]李启良,杨志刚.计算流体力学在气动一声学风洞设计中的应用[J].空气动力学学报,2009,27(3):373-377.
[12]张弘,于正平.受电弓空气动力学模型及风洞试验研究[J].中国铁道科学,1995,16(1):37-49.
[13]张曙光.高速列车设计方法研究[M].中国铁道出版社,2009.
[14]蔡国华.高速列车受电弓气动特性测量[J].流体力学实验与测量,2004,18(1):53-56.
