浅谈中学常见数学解题策略

徐礼礼 江苏省南通高等师范学校 225006

浅谈中学常见数学解题策略

徐礼礼 江苏省南通高等师范学校 225006

美国著名数学家G.波利亚说：“中学数学教学的首要任务，就在于加强解题训练.掌握数学就意味着解题。”美国数学家哈尔莫斯说过：“数学的真正组成部分是问题和解.”数学教学的一个很重要的任务，就是教学生如何解数学题，教会学生“数学地思维”.学数学，就要解数学题，数学解题学习对学生巩固知识、培养素质、发展能力都有极其重要的意义.而在解题教学中，解题策略的教学则是关键.解题策略是指解答数学问题时总体上所采取的方针、原则和方案.解题策略不同于具体的解题方法，它是指导方法的原则，是对解题途径的概括性认识和宏观把握，体现了选择的机智和组合的艺术，因而是最高层次的解题方法。下面就应用知识阶段的解题策略谈一些粗浅的认识。

一、模式识别

当主体接触到数学问题之后，首先要辨别题目的类型，以便与已有的知识经验发生联系，然后再确定解决问题的思路.这种首先进行归类辨别的策略便是模式识别策略。

例1 已知等差数列｛an｝，Sn为其前n项和，且S10＝S20，则S30等于多少？

解 由题意可知，

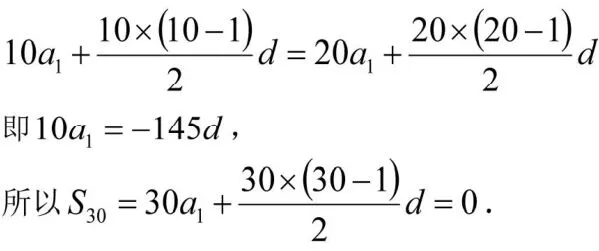
分析 阅读题目后可直接识别此题为是解数列问题，利用解决此类问题的模式，考虑采用基本量法，即求出等差数列中的基本量a1和d，问题就一定会迎刃而解.当然，本题还有其他更为简单、巧妙的解法，但在这里更需强调的是通性通法，因为它体现了中学数学教学中的“基本问题”思想，渗透了“算法”思想，即将同类问题转化为标准问题，然后用标准的程序去解决它。实际上，中学数学中还有很多类似的“基本问题”，在教育教学过程中要有意积累模式，加强识别，这样才能做到“以不变应万变”。

二、化归转化

当我们面对的数学问题不能用已知模型加以解决时，就会考虑其他意义上的解题策略，其中首要的就是化归转化策略，化繁为简、化生为熟、化新为旧、化未知为已知，这是人类认识的基本规律.化，就是变化原问题，转化原问题，变换原问题；归，说的是变化、转化、变换原问题是有目的、有方向的，其目的是变化出一个已知数学模型，就是通过变化使新问题转化为解决过的问题。

例2 设a，b，c都是正数，且3a=4b=6c，试证：

解 对3a=4b=6c同时取对数有

分析：由于已知等式中的a，b，c都是指数，不便于运算。通过取对数这一等价转化手段，将指数幂运算转化为乘法运算，降低了运算难度。实际上，取对数运算、换元、引进坐标系、设计数学模型、构造函数等均是化归转化的常用手段。

三、差异分析

通过分析条件与结论之间的异同、并不断减少目标差来完成解题的策略，称为差异分析.使用差异分析通常要求通过分析题目的条件与结论中所出现的数量特征、关系特征、位置特征等去寻找目标差，一旦出现目标差主动作出减少目标差的反应，多次减少目标差使得目标差的减少能积累起来。

例3

∴得证。

分析：通过观察、分析求证式左、右两边的差异，发现两个目标差：一个是角的差异，另一个是函数名的差异，解题时从分析目标差入手，向着减少目标差的方向努力.差异分析法是“综合——分析法”的一种特殊形式，在三角恒等式或不等式的证明中应用广泛。

四、正难则反

解决数学问题时，大多是从条件出发进行正面顺向思考。然而，事物往往是互为因果的，具有双向可逆的特征。如果正向思维有困难时就逆向思维，顺向推导有困难时就逆向推导，直接证明有困难时就间接证明。

证明 假设 不是无理数，而是有理数，

由于在p2的素因数分解中，有偶数个2（或0个2），在q2的素因数分解中，有偶数个2 （或0个2），在6的素因数分解中，有1个2。

可见，在6q2的素因数分解中，有奇数个2。

分析：由于已知条件太空、太少，以至于正面直接推导“举步维艰”，故可考虑采用“正难则反”的策略。事实上，这一策略在一方面是对正向思维的背叛，同时又离不开正向思维的“协同作战”，所以，应该是“正反相辅”。这一策略反映了原因与结果的辩证统一，肯定与否定的辩证统一，有限与无限的辩证统一，证实与证伪的统一。

五、以少胜多

不少数学问题往往涉及多个变量，多个变量往往难以控制，但这些变量之间又存在一定的联系，抓住这种联系，用变换的方法，以较少的变量甚至一个变量来控制多个变量，往往使问题迎刃而解。

例5 设a，b∈R,a2+4b2=8，求 a+b的最大、最小值。

解

分析：要求a+b的最大、最小值，a，b都是变量，但a，b又满足a2+4b2=8，如果将变量变换成一个，则问题就变为熟悉的问题.为此可以令，转化为三角函数的最值问题。

六、以退求进

以退求进解证数学问题的策略是：把一个不能马上解决的问题，通过弱化或更改条件，退到能够解决的程度，找到问题的突破口或解法思路，以求原问题的完满解决，这是一种辩证思维，即运用联系转化思想，将问题按适当方向后退到能看清关系或悟出解法的地步，再通过后退后相关问题的求解推知原问题的解法.华罗庚教授曾指出：“善于退，足够地退，退到最原始而不失重要性的地方，退到我们容易看清问题的地方，是学好数学的一个诀窍”。

证明 作△ABC外接圆的直径AD，BE。设半径为R，连CE，DC，BD。

并分别设其长为x，y，z，则

分析：本题通常做法是运用两角和的余弦及三角函数的和差化积公式来解，显然比较繁琐。仔细观察题目，我们发现题中涉及的角为锐角，我们可以退回到初中阶段所学过的三角函数的定义上来解决。

发挥学生的主体性，使学生学会学习，是教学工作的重中之重.解题策略的教学是解决这一问题行之有效的方法.教师应将解题策略的教学贯穿到课程具体内容的教学过程中，与学生的整个学习过程紧密结合，使学生有大量的实践机会，从而充分发挥解题策略对学习的促进作用。

[1]罗增儒.数学解题学引论［M］.陕西：陕西师范大学出版社.2008.

[2]李维.认知心理学研究［M］.杭州：浙江人民出版社.2004.

[3]张雄，李得虎.数学方法论与解题研究［M］.北京：高等教育出版社.2003.

10.3969/j.issn.1001-8972.2010.21.132