应用于变频空调系统的无速度传感器矢量控制研究＊

兰州理工大学 电信学院（甘肃兰州730050） 李晓英 王言徐

1 引言

变频空调通过调节压缩机电机转速来改变压缩机单位时间的排气量，从而改变制冷系统中循环的制冷剂流量，达到调节环境温度的目的。能效比是衡量变频空调性能的重要指标。通常压缩机电机低速运行时能效比高，而高速运行时能效比低[1]。然而，当电机低速运行时，由于压缩机吸气、压缩、排气的物理过程会引起较大的转矩脉动，从而导致压缩机电机的转速波动。可见，需提高能效比和降低转速波动之间存在矛盾。变频压缩机普遍采用V/f恒定的开环控制方法，由于没有速度闭环，低速范围转速波动以及由此带来的压缩机震动和噪声问题更为突出。要减小压缩机转速波动，需引入速度反馈，然而压缩机的机械结构决定了很难在其内部安装速度传感器。

为解决这一问题，本文采用无速度传感器矢量控制方案，不引入速度传感器，用转速估计算法获得速度信号进行闭环控制，以改善变频空调控制系统的动态响应，减小由于转速波动带来的压缩机震动和噪声。无速度传感器矢量控制的关键在于转子磁链的观测和转速估计，针对这两个核心问题，本文构造了改进电压型磁链观测模型，并基于PI自适应控制方法实现转速估算。

2 转子磁链观测

由于按转子磁场定向时，定子电流的励磁分量和转矩分量之间可实现完全解耦，且转子磁链的表达形式最为简单（仅与定子电流的励磁分量有关），故本文采用按转子磁场定向的矢量控制策略。要实现按转子磁场定向的矢量控制，必须获得转子磁链信号，即必须对转子磁链进行观测。转子磁链观测的准确与否，直接影响到电机定子电流中的励磁分量和转矩分量能否实现真正解耦[2，3]。因此转子磁链的准确定向及观测至关重要。在实际系统中，通常借助于容易测量的电压、电流等信号构造转子磁链模型来间接计算磁链的大小与相位。

异步电动机在静止两相坐标系下的电压方程为：

式中，usα、usβ分别为 α 轴和 β 轴的定子电压；isα、isβ分别为 α 轴和β 轴的定子电流；Ψrα、Ψrβ分别为 α 轴和 β 轴的转子磁链；Rs、Rr分别为定子电阻和转子电阻；Ls、Lr、Lm分别为定子电感、转子电感和互感；Lsσ=σLs为考虑漏感时定子的等效电感，σ为漏感系数；Tr=Lr/Rr为转子时间常数；ωr为转子角速度；p为微分算子。由式（1）可得常用的两种转子磁链观测模型[1]：

比较式（2）、式（3）不难发现，相对于电流模型，电压模型具有算法简单、不含转子电阻等优点；并且电压模型仅通过测量定子电压、电流即可估计转子磁链，不需要转速信息。因此，电压型转子磁链观测模型比较适用于无速度传感器变频调速系统。

虽然电压模型在高速时性能较好，然而电压模型中磁链是由反电动势积分得到的，在电机低速运行时产生的反电动势较小，影响磁链观测的准确性；此外，模型中的纯积分环节在实际应用时会带来直流漂移和误差累积等问题，低速时会降低磁链观测的精度，进而会使得整个控制系统性能下降。当电压模型应用于变频空调控制系统时，解决纯积分环节带来的直流漂移和误差累积等问题、提高低速时磁链观测的精度显得尤为重要。

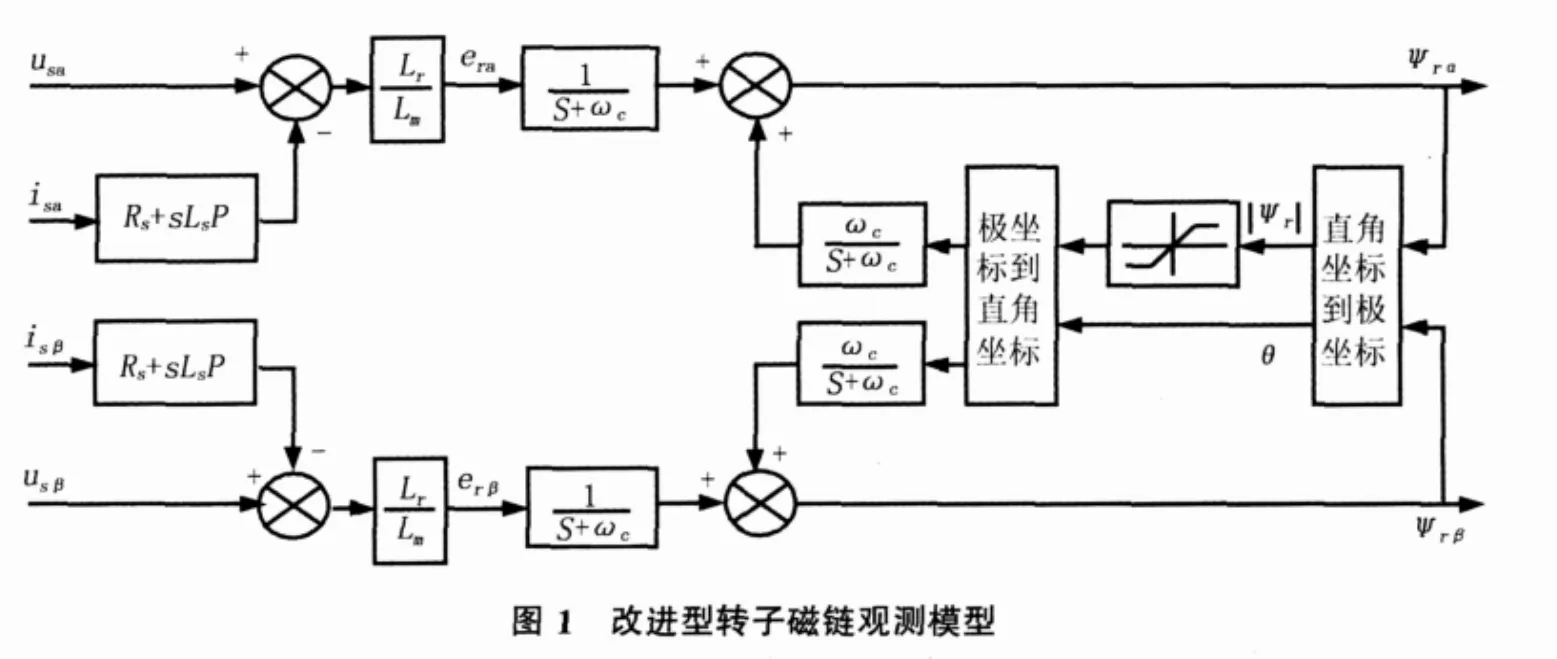
在保持电压模型中、高速的良好性能基础上，本文对纯积分环节加以改进，引入一种带限幅反馈环节的积分器代替纯积分器。改进型转子磁链观测模型如图1示。

图中 erα、erβ分别为α轴和β轴的转子反电动势，表达式如下：

｜Ψr｜、θ分别为转子磁链的幅值与位置角：

改进型磁链观测模型中，带限幅反馈环节的积分器在消除纯积分器直流漂移的同时不会引入转子磁链的幅值与相位误差。

3 转速估算

转速估计是无速度传感器矢量控制系统的又一核心问题。国内外已有多种估算转速的方法，如PI自适应法、直接计算法、模型参考自适应法（MRAS）、高频注入法及扩展卡尔曼滤波法等[1,3]。在变频调速控制系统中，宜采用速度估计的稳态特性和动态特性综合指标较高的估算方法，还应考虑到实现起来简单。高频注入法及扩展卡尔曼滤波法由于计算量庞大，在实际系统中一般不采用。本文采用基于PI调节器的自适应法估计转子转速。

根据电机的机电运动方程式：

考虑控制过程中 Ψrd保持恒定，则 Te由 isq决定，转矩的误差信号可以由给定转矩电流分量与实际响应 isq的差值反映出来，将（－ isq）送入 PI调节器，输出即为转速的估算值 ωr，即

这种基于PI调节器的自适应速度估计法可以认为是模型参考自适应（MRAS）法的变形，在模型参考自适应法的基础上采用PI自适应机制，从电流转矩分量的误差信号得到转子速度的估计，其结构较模型参考自适应法简单[4]，如图2所示。

图中，可将转子磁通观测得到的 Te看作参考模型，而看作可调模型，利用两模型输出值的误差来调整中的 ωr，直到两模型的输出值相等，即－Te=0时，认为 ωr为实际转速。PI调节自适应法转速估算关系式：

式中，KP、KI为PI调节器参数。

4 无速度传感器矢量控制系统仿真

4.1 系统结构

基于上述转子磁链观测以及转速估计原理的变频空调矢量控制系统结构如图3示。

图中，速度调节器ASR、转矩调节器ATR以及磁通调节器AΨR均采用PI控制。磁链观测模块采用带限幅反馈的改进电压型磁链观测模型，速度推算模块采用PI自适应法进行转速估算。变频空调压缩电机由三相SVPWM电压型逆变器供电。

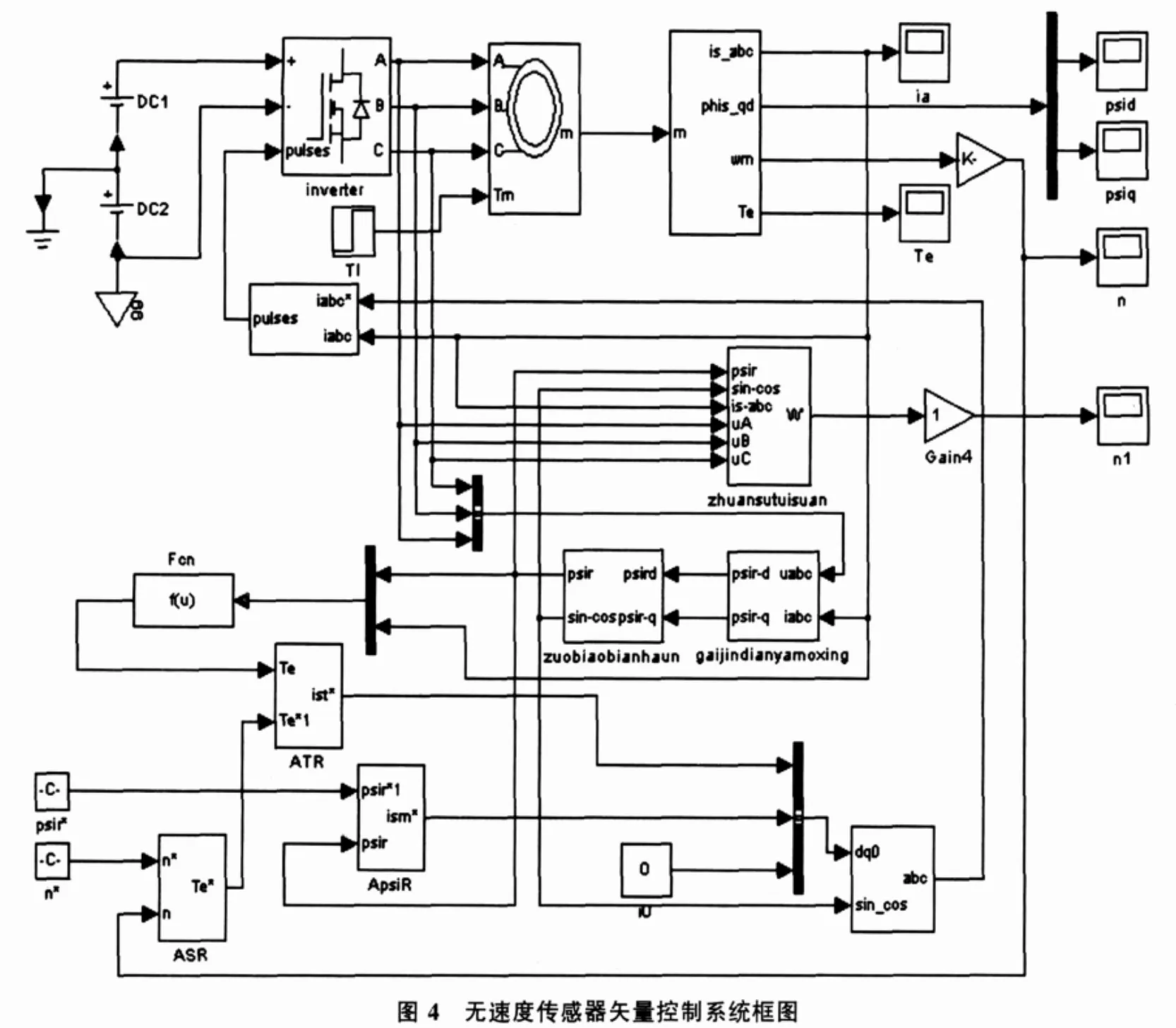
在Matlab/Simulink环境下，建立无速度传感器变频空调矢量控制仿真模型如图4所示：

4.2 仿真波形与结果分析

系统仿真所用电机为Y接三相异步电动机，参数设定如下：额定电压 380V，频率50Hz，极对数 pn=2，转动 惯 量 J=0.002kg/m2， 定 子 电 阻 Rs=0.384Ω，定子电感 Ls=0.002mH， 转 子 电 阻Rr=0.836Ω，转子电感Lr=0.002mH， 互 感Lm=0.0891mH。模型的仿真算法采用Ode23tb[5]，空载起动，在1.0s时突加额定负载，仿真时间设为2.5s。考虑到空调压缩机

有最低频率限制[1]，故设定参考转速为600r/min进行仿真。转速、转矩、电流以及磁链的仿真波形如图5所示：

图5（a）所示转速响应曲线表明，起动时转速略有超调，由于PI调节器的影响，动态时估计转速与实际转速有一定的差异；但稳态时的速度辨识精度较高，0.5s以后估计转速与实际转速几乎完全重合。图 5（b）、（c）分别为转矩、定子电流仿真波形，起动时转矩及电流波动较大，但转矩响应较快，稳态时 ，转矩、电流的波动都很小。图5（d）给出了转子磁链α分量的仿真波形，由于改进了转子磁链电压模型中的纯积分环节，磁链观测较准确，从图中可以看出，动态时转子磁链波动小，幅值、相位稳定。

5 结论

本文通过改进电压型转子磁链观测模型以及PI自适应速度辨识构建了变频空调无速度传感器矢量控制仿真模型。仿真结果表明：系统动态响应较快，稳态时的速度辨识精度高，磁链观测准确。将无速度传感器矢量控制应用于空调变频控制系统，可降低压缩机转速波动，显著减小震动及噪声。

[1]石文星，彦启森，陈华俊，王宝龙.论变频空调性能评价体系[J].暖通空调，2004，34（5）：52 ～ 58.

[2]冯垛生，曾岳南.无速度传感器矢量控制原理与实践[M]第二版.北京：机械工业出版社，2006.

[3]李永东.交流电机数字控制系统[M].北京：机械工业出版社，2003.

[4]Young Ahn Kwon,Sung Hwan Kim,A New Scheme for Speed Sensorless Control of Induction Motor[J].IEEE Trans.On Industrial Electronics,2004,51（3）:545～550.

[5]洪乃刚.电力电子和电力拖动自动控制系统的MATLAB仿真[M].北京：机械工业出版社，2006.