基于卡尔曼滤波器的零速修正技术在导弹发射车中的应用研究
2010-09-20淮阴师范学院淮安223001杨裕翠俞阿龙
淮阴师范学院(淮安 223001) 杨裕翠 俞阿龙
南京航空航天大学(南京 210016) 祝燕华
1 引言
现代战争中,为了提高导弹武器系统的生存能力和战斗能力,采用随机点快速发射(机动发射)是一项重要的措施。传统的定点发射方式,需预先在发射场坪标定出大地坐标,这既不适用于任意点发射,又不利于缩短反应时间;而机动发射带来的问题是如何能快速、精确地测定发射点的地理坐标位置。
目前,用于发射车定位的技术主要有惯性定位和卫星定位技术,本文所研究的问题是针对惯性定位而言的。惯性定位系统能实时自主地提供载体的姿态、速度和位置信息,但是它的不足之处在于惯性器件引起的定位误差随时间积累,因而长时间独立工作后的定位信息的误差大[1,2]。
本文提出了将零速修正技术应用在导弹发射车车载捷联惯导系统中,采用卡尔曼滤波对惯导误差进行实时计算并补偿,提高了惯导的定位精度,可以实现随机点的快速定位。
2 基于卡尔曼滤波的零速修正算法
零速修正(ZUPT)技术是利用载体停车时惯性系统的速度输出作为系统速度误差的观测量,进而对其它各项误差实现校正的技术。具体的实现过程为,惯导系统启动并经初始对准后,从一个已知坐标点出发,每隔一定时间停车进行零速修正,到达待测点后,在短时间内(如1分钟)即可获得该点的坐标数据。这种方法除需要一个起始坐标点外,途中不需要任何外部信息,因此将其应用在导弹发射车上,对于现代战争环境下的应用具有十分明显的优势。
采用零速修正进行误差估计的算法有很多[2],如曲线拟合、最大似然估计和卡尔曼滤波等。曲线拟合和最大似然估计方法由于模型简单且对时间间隔的依赖性大,所以估值精度较低;而卡尔曼滤波是线性最小方差的无偏估计,估值精度较高,并且从误差特性考虑。本文针对某国防项目的实际研究需要,采用基于实时卡尔曼滤波的零速修正误差估值算法,分析零速修正时不同时间间隔对系统性能和精度的影响。
2.1 惯性仪表误差模型
惯性仪表误差主要包括安装误差、刻度系数误差和随机误差,认为非随机性误差已通过多位置量测等方法进行校正,这里仅考虑随机误差。
(1)陀螺漂移误差模型

式中,!b为随机常数;!r为一阶马尔可夫过程;"g为白噪声。
假定三个轴向的陀螺漂移误差模型相同,均为
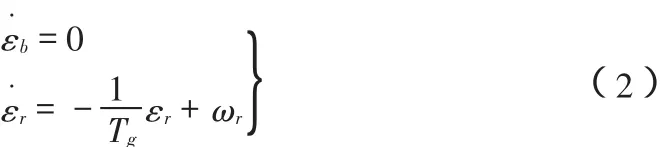
式中,Tg为马氏过程的相关时间,"r为马氏过程的白噪声。
(2)加速度计误差模型
考虑其为一阶马尔可夫过程,且假定三个轴向加速度计的误差模型相同,均为

式中,Ta为马氏过程的相关时间,ωa为马氏过程的白噪声。
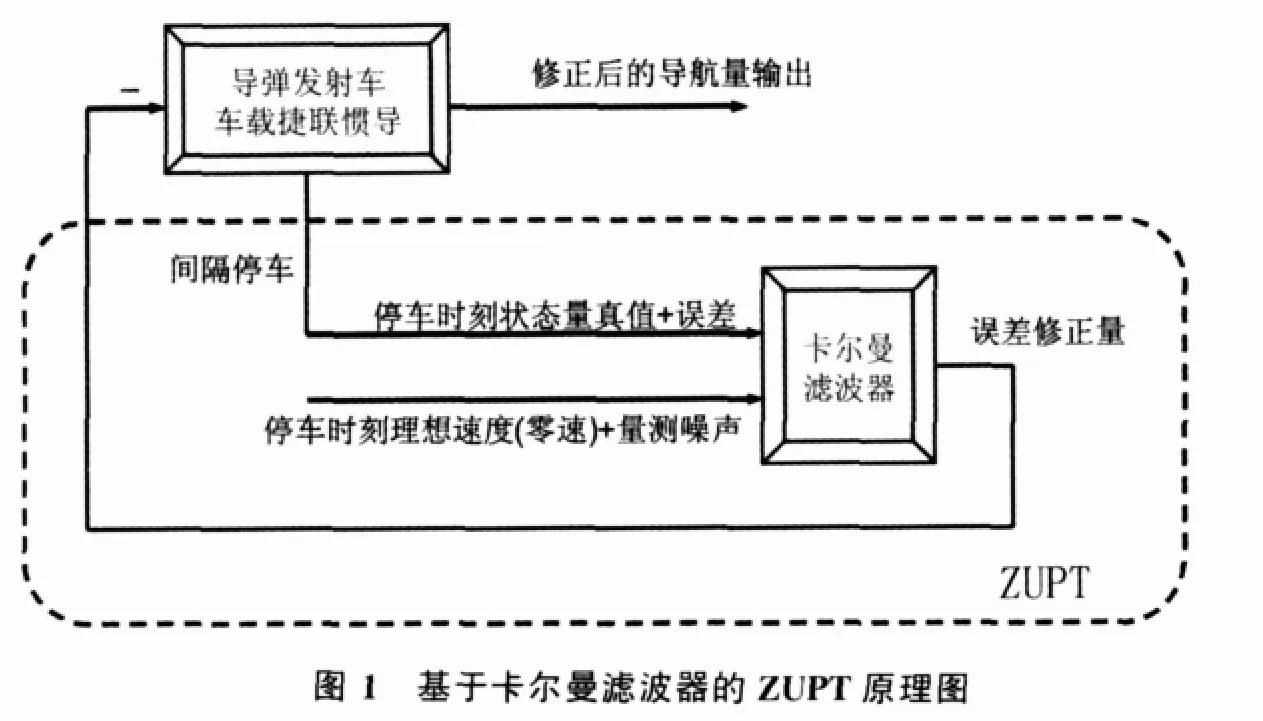
2.2 基于卡尔曼滤波器的ZUPT模型
基于卡尔曼滤波器的ZUPT模型的基本原理如图所示:
发射车车载捷联惯导系统的误差模型可用下列状态方程描述:
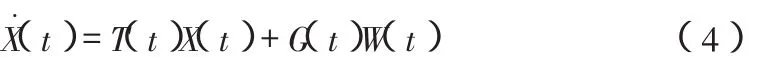
上式中,状态向量可分为两个向量来考虑

其中,X1为惯导系统的九个导航误差状态向量,X2为九个传感器误差的增广状态向量,如下所示:
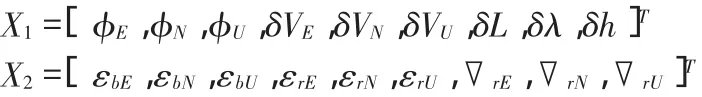
T(t)为18阶的系统矩阵,G(t)为18×9的系统噪声系数矩阵,W(t)表示系统噪声。
在导弹发射车停车时,真实的速度输出在东、北、天方向的分量都应该为零,那么惯导的速度输出必然就是速度误差。所以,以惯导系统的速度输出作为观测量,建立下面的观测方程:

其中,V(t)表示量测噪声,H值应为:

于是经离散化后,卡尔曼滤波器有下列方程组
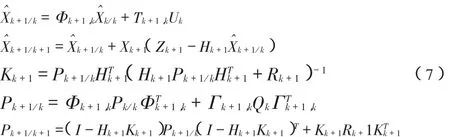
式中:Q和 R分别为系统噪声方差阵和量测噪声方差阵,只要给定初值,便可利用上式递推得到各状态的最优估计并进行实时的补偿[3,4]。
3 仿真分析
3.1 仿真流程图及其初始条件
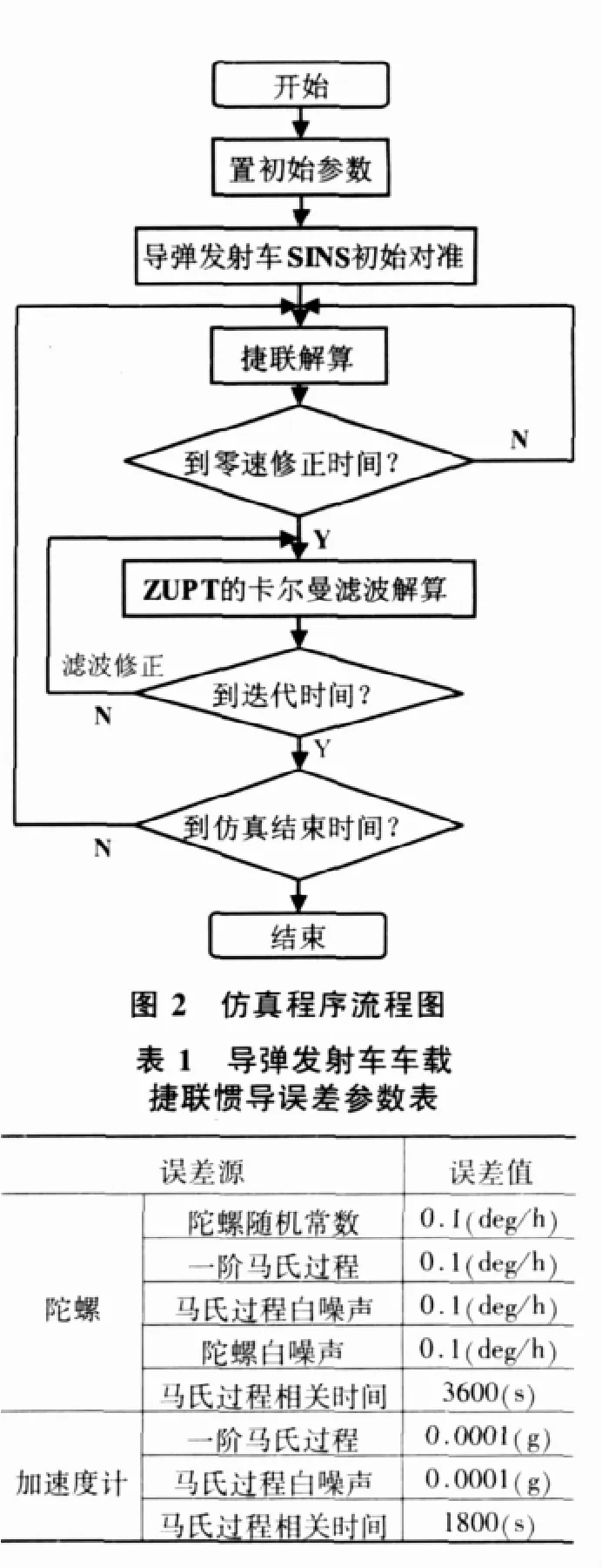
导弹发射车捷联惯导系统零速修正仿真流程图给定如下:
导弹发射车纯捷联惯导误差参数如表1所示:
3.2 系统仿真和结果
导弹发射车初始位置为东经118.0°,北纬 32.0°,海 拔 高 度1000.0米,初始姿态水平,初始航向角为0.0°。
导弹发射车的运动包括:平直加速、平直匀速行驶、平直减速、停车这五个状态。发射车每隔一定时间T重复这一运动过程。在停车位置进行卡尔曼滤波的零速修正,得到状态的最优估计并进行闭环实时补偿,停车时间即为卡尔曼滤波迭代时间τ。
要想从根本上提高民办高校实验建设和教学管理水平,既满足教学需求,又能做到为学生负责,为国家提供自主创新的人才。需要民办高校不断深化教育教学改革,对实验教学管理提出更高的要求,并在此基础上不断培养高素质、高水平的技术应用型人才。但是,现在的民办高校还不能更好的适应社会的发展,实验室的管理水平还不够科学规范,实验室的利用率没有充分挖掘,不能更好的服务于学生。要提高教学质量,需要进一步解决实验教学中存在的不足。
国外资料表明,零速修正的停车间隔一般为3~5分钟[5]。为了考察停车间隔时间T对零速修正性能的影响,本文设计了三条航迹进行仿真比较,这三条航迹中发射车所经过的路径是完全相同的,则车辆的行驶里程也必然相同,不同点在于停车间隔T,具体说明如下:
*航迹1:停车间隔T=300s,车辆行驶过程中的加速度为5.00m/s/s,最大速度为25.0m/s;
*航迹2:停车间隔T=500s,车辆行驶过程中的加速度为4.96m/s/s,最大速度为20.6m/s;
*航迹3:停车间隔T=900s,车辆行驶过程中的加速度为4.12m/s/s,最大速度为24.8m/s;
行驶里程共73.75公里,仿真时间均在1小时左右,在停车位置滤波迭代40s进行修正。
为了考察以及比较零速修正的性能,我们给出整个仿真过程导弹发射车理想经纬度位置曲线(曲线1)、导弹发射车上纯捷联惯导解算得到的经纬度位置曲线及其误差曲线(曲线5),以及三条不同停车间隔的SINS+ZUPT解算得到的经纬度位置曲线及其误差曲线(T=300s时,曲线2;T=500s时,曲线 3;T=900s时,曲线 4),如图 3、4和 5所示:上面的曲线图不仅直观地反映了零速修正技术大大降低了发射车的位置误差,提高了捷联惯导的定位精度,而且说明了零速修正的有效性会随着停车间隔时间的增长而降低。
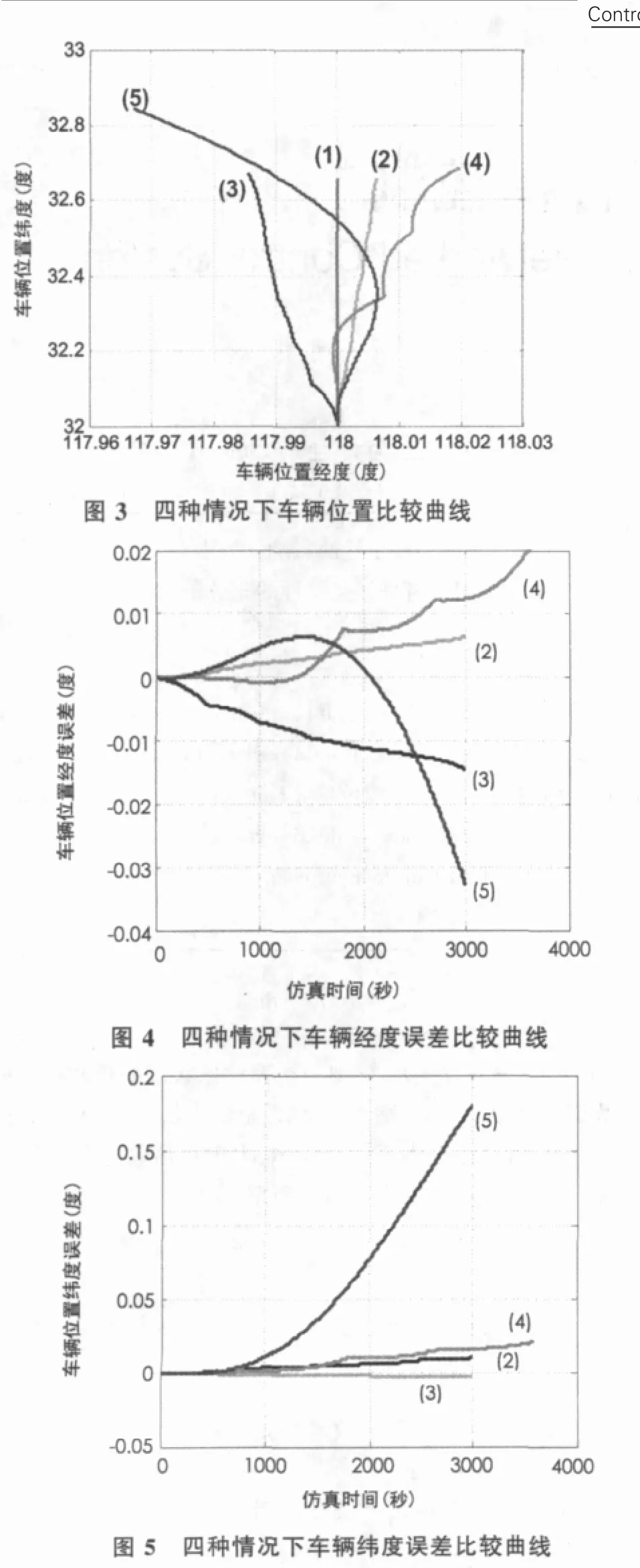
?
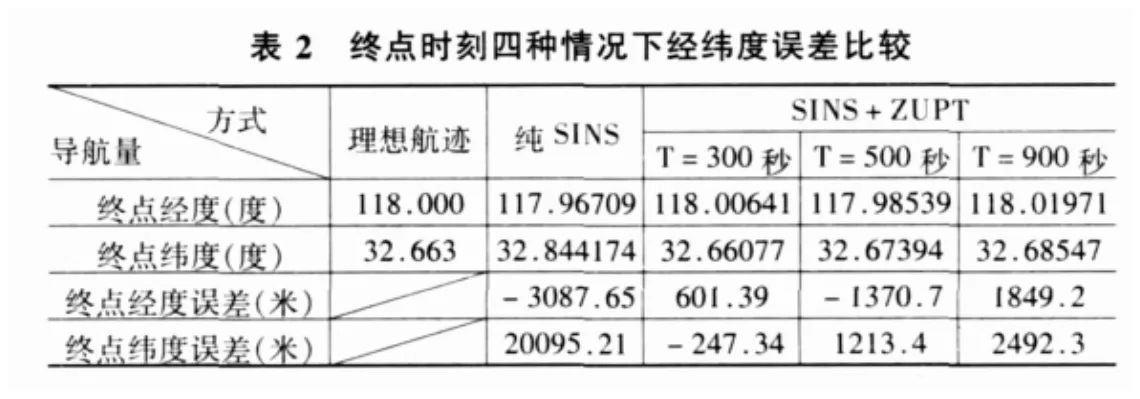
由于导弹发射车零速修正的目的在于实现导弹的随机点快速发射,即要能以较高的精度给出发射车到达发射点时刻的位置,为此给出四种情况下发射车到达终点时刻的定位数据,如表2所示:
分析表格中的数据可知,停车间隔T=300s时终点经度、纬度误差都在500米左右,相对纯捷联而言,精度提高了100倍,随着T的增加,精度降低,到T=900s时终点经度、纬度误差已达2000米以上,零速修正的效果已经不是很显著。以本文仿真所给出的IMU精度来讲,停车间隔在10分钟以内SINS+ZUPT的定位精度是比较高的。
一方面,对于导弹随机发射点的定位精度来说,显然停车间隔T越短越好;另一方面,对于发射车发动机而言,频繁加速减速停车会增重其负担,停车间隔T又不易太短。所以,在工程实践中,应同时从这两个方面考虑,并结合IMU的精度,选择合适的停车间隔时间。
! 结论
本文提出了将零速修正技术应用在导弹发射车车载捷联惯导系统中,并采用卡尔曼滤波方法对惯导误差进行实时计算并补偿,经过多次的仿真验证,均表明卡尔曼滤波的零速修正其有效性随着停车间隔时间的增长而降低,从原理上分析也可知,一方面是由于惯导系统位置误差快速增长;另一方面,惯导速度误差与位置误差变化的相关性随着停车间隔T的增大而降低。因此在工程实践中应综合考虑定位精度要求和导弹发射车行车的需求,选择合理的停车间隔。
综上,本文提出的卡尔曼滤波的零速修正能在较大程度上减小惯导的定位误差,解决了导弹武器系统发射车的随机点快速发射问题,而且通过对零速修正间隔时间不同对惯导性能的影响比较,在工程实践中具有重要的参考价值。
[1]李辉,王子滨.国外GPS/INS复合制导技术的发展[J].现代防御技术,2004,32(2):42 ~ 46.
[2]高钟毓,王进,董景新,赵长德.惯性测量系统零速修正的几种估计方法[J].中国惯性技术学报,1995,3(2):24 ~ 29.
[3]杨大烨,谢天怀,胡宝余.捷联惯导系统初始姿态和仪表误差标定迭代算法研究[J].中国惯性技术学报,2002,10(3):15 ~ 20.
[4]Xiaoying Kong.INS algorithm using quaternion model for low cost IMU.Robotics and Autonomous Systems,2004,46(4):221 ~246.
[5]Hu Shan,Luo Jian-Jun,Yuan Jian-ping.Development of simulation system of INS/DS integrated system.Journal of System Simulation,2004,16(9):57~60.
[6]马小艳,富立,王玲玲.不等间隔角速率输出的捷联航姿算法研究[J].中国惯性技术学报,2006,14(3):18~22.
[7]Bortz J E.A new mathematical formulation for strapdown inertial navigation[J].IEEE Transactions on Aerospace and Electronic Systems,1971,7(1):61~66.
[8]祝燕华,刘建业,钱伟行,赖际舟.低成本捷联惯导系统的静基座快速精对准方法[J].上海交通大学学报,2008,32(05):32 ~37.
[9]Miller R B.A new strap - down attitude algorithm[J].Journal of Guidance,Control,and Dynamics,19183,6(4):287~291.
