颗粒链在振动条件下的行为研究

骆子喻,张雷锋,鲍德松

(浙江大学物理系,浙江杭州310027)

颗粒链在振动条件下的行为研究

骆子喻,张雷锋,鲍德松

(浙江大学物理系,浙江杭州310027)

采用实验方法研究打结颗粒链在外部激振下解结过程与激振源以及颗粒链长度的关系.实验结果表明颗粒链结解开所需的时间与振动频率有关,颗粒链解结存在截止频率和最佳振动频率;颗粒链解结时间与链长之间呈非线性关系.同时采用Monte Carlo时步模拟的方法,对珠链解结的动力学模型进行仿真.

颗粒物质;颗粒链;振动频率;Monte Carlo

1 引 言

颗粒物质是我们生活中常见的物质类型.对于单个颗粒的运动规律已经可以用运动方程进行精确地描述,但对于大量颗粒组成的非线性复杂离散系统,目前还仅仅停留在定性描述阶段,所以对颗粒物质的研究在最近十几年来已经引起物理学界的广泛兴趣[1-2],对宏观颗粒链的研究,可以为聚合物分子链、DNA分子等的动力学性质研究提供支持.颗粒链结的解结时间与外加振动的振幅、振动频率、颗粒链长度、颗粒半径、颗粒密度等诸多因素相关,本研究是在振幅、颗粒半径以及颗粒密度不变的条件下,研究解结时间与颗粒链长度及振动频率之间的关系,同时采用MonteCarlo时步模拟的方法,对珠链解结的动力学模型进行仿真.

2 实验条件及实验装置

实验采用直径为(5.00±0.04)mm的中空塑料颗粒,用尼龙线致密串成颗粒链,颗粒链两端棉线打结固定,共留出约半个珠子的空隙.振动驱动源采用E1641B1型函数信号发生器、音频功率放大器、12寸低音扬声器以及XJ4328示波器搭建.颗粒链长度从31颗颗粒至40颗颗粒不等,驱动频率在12～70 Hz范围调节.实验装置示意图如图1.实验过程中保持输入至扬声器的信号幅度不变,信号强度用示波器实时监测.

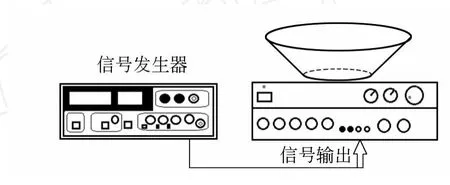
图1 实验装置示意图

3 实验结果

3.1 颗粒链结解开时间与振动频率之间的关系

在测量振动频率与解结时间关系时,实验选取链长为31颗颗粒的颗粒链,振动信号频率通过信号发生器可连续调节,信号振幅由功放控制并由示波器实时监测.由于每次测量结果存在离散,实验时在每个频率下重复测量20次,所以实验所测得的时间为20次测量的平均值.从而得到颗粒链结解开时间与外加振动频率之间的关系,如图2所示.由图可知,在颗粒链长度固定的条件下,颗粒链解结效率(解开链结所需时间的倒数)与外加振动频率呈非线性关系,最高解结效率出现在外加频率为40 Hz的条件下,而且颗粒链结只能在某一频率范围内才能解开,在实验条件下,解结频率范围在16～55 Hz之间.另外,我们发现在振动频率为20 Hz附近也有较高的解结效率,这可能是在此频率下系统产生共振现象.

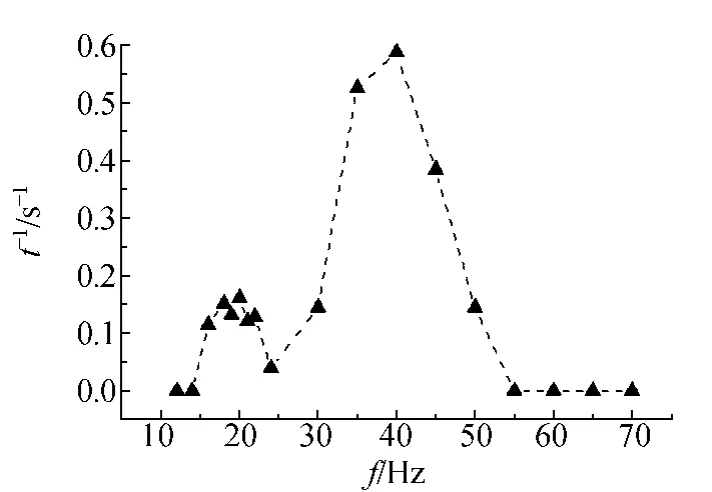
图2 振动频率与解结效率之间的关系

3.2 颗粒链解结时间与颗粒链长度的关系

选取长度为31～40颗的珠链,对解结时间随珠链长度变化的关系进行测量,实验结果如图3所示.发现解结时间与颗粒链长度存在非线性关系,对解结时间取对数后得到结果如图4所示,发现lnt与颗粒链长度基本呈线性关系.由图4中线性拟合结果不难发现,lnt=0时,直线在横轴的交点为24.其物理意义为:长度为24颗珠子的珠链解结时间为1 s.对于平均1 s内解结的珠链,可以近似认为珠链在开始振动时就已经解开,而实际上24颗颗粒正好对应构成一个单结的最小颗粒数,这与拟合结果完全吻合.

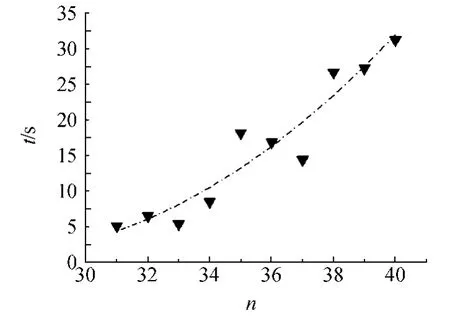
图3 颗粒链解结时间与链长度之间的关系

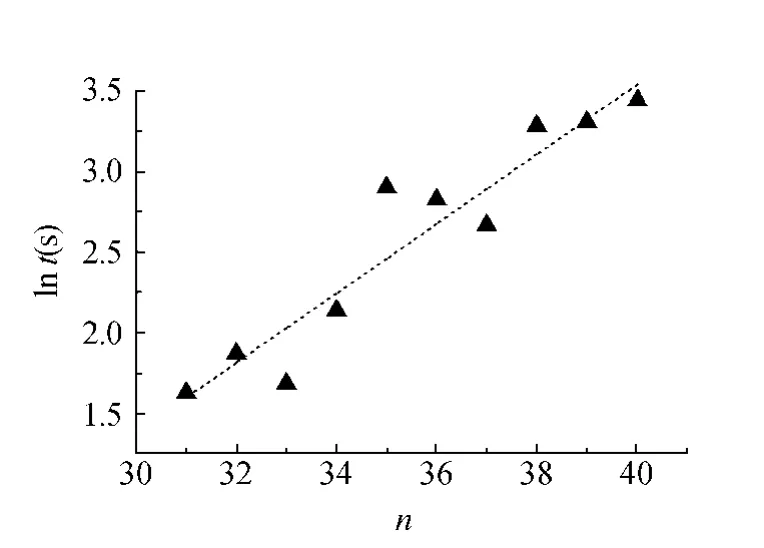
图4 颗粒链解结时间的自然对数lnt与颗粒链颗粒数之间的关系

3.3 颗粒链解结过程的动力学模型及其模拟结果

由于一维颗粒链解结过程非常复杂,所以尝试构建简单的物理模型进行解释.考察颗粒链的拓扑结构,如图5所示.不难发现,拥有1个单结的颗粒链存在A和B两个节点.将这2个节点视为链上激发出的准粒子,节点可以在链条上行走.开始时节点A和B相邻.此后,随机选择A或B中的1个,并随机选择左或右方向,使A或B以一定的概率(概率与振动强度,势垒高度等因素相关,振动强度越大,则翻越概率越大,势垒高度越大,则翻越概率越小,计算时,由于振动强度与势垒高度不变,我们将翻越概率定为0.5进行计算)向该方向移动1格,并将此过程视为1个时间步长(A,B位置不可互换),直至一个端点走出链一端时,颗粒链被解开.基于这样模型,尝试使用MonteCarlo时步模拟的方法,对颗粒链解结的动力学模型进行仿真.在一定振动强度下,颗粒链中的颗粒拥有平均动能E,而一个端点要移动到邻近格点,需要翻过能量为mgr的势垒.在此基础上,得到了如图6所示仿真结果.图6中纵坐标为完成1 000次自由行走的总步数,即对应解结时间,为构成单结的最少颗粒数.对于其中mgr的影响,由于实验条件上的限制,我们只尝试了几种质量、半径的差异较大的颗粒,实验结果定性符合上述假设.

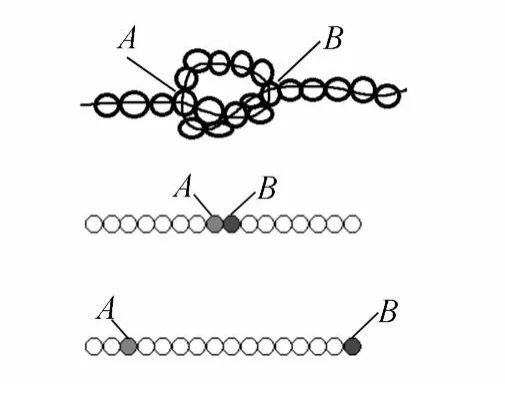
图5 自由行走模型示意图

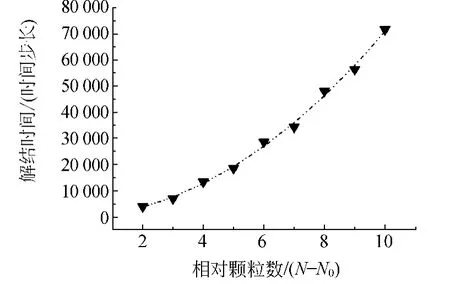
图6 MonteCarlo时步模拟结果

4 实验结论

实验测量了颗粒解结效率与振动频率之间的关系、颗粒链解结时间与颗粒链长度之间的关系以及采用Monte Carlo时步模拟方法对颗粒链解结的动力学模型进行仿真,结果发现:颗粒链结只能在某一振动频率区间内解开,在我们的实验条件下频率范围为16～55 Hz,颗粒链解结效率与振动频率存在非线性关系,而振动频率为40 Hz时出现最佳解结效率;颗粒链解结时间与链长度之间呈指数关联;通过构建精简的自由行走模型,得到了与实验结果相符合的计算机仿真结果.

[1] Ben-Naim E,Daya Z A,Vorobieff P.Knots and random walks in vibrated granular chains[J]. Phys.Rev.Lett.,2001,86:1414.

[2] Hastings M B,Daya Z A,Ben-Naim E,et al.Entropic tightening of vibrated chains[J].Phys. Rev.E,2002,66:025102.

[3] 陆坤权,刘寄星.颗粒物质[J].物理,2004,33(9/ 10):629-635.

Unknotting of vibrated granular chains

LUO Zi-yu,ZHANG Lei-feng,BAO De-song
(Department of Physics,Zhejiang University,Hangzhou 310027,China)

The unknotting process of vibrated granular chain is experimentally studded.The results show that the time of unknotting relies on the frequency of vibration.There are a cut-off frequency and a most efficient unknotting frequency.The relation between the length of the granular chain and the unknotting time is nonlinear.Monte Carlo calculation is adopted to simulate the dynamic process.

granular matter;granular chains;vibration frequency;Monte Carlo

O32

A

1005-4642(2010)12-0036-03

[责任编辑:郭 伟]

“第6届全国高等院校物理实验教学研讨会”论文

2010-03-16;修改日期:2010-05-24

浙江省教育厅项目(No.Y200804093);2009年度“国家大学生创新实验计划”项目

骆子喻(1987-),男,上海人,浙江大学物理系2006届本科生.

指导教师:鲍德松(1964-),男,浙江余杭人,浙江大学物理系高级工程师,学士,从事颗粒物质方面的研究.