用光子纠缠源验证Bell不等式

孙文博,王合英,陈宜保,何元金

(清华大学物理系,北京100084)

用光子纠缠源验证Bell不等式

孙文博,王合英,陈宜保,何元金

(清华大学物理系,北京100084)

以Bell不等式的推广形式CHSH不等式为理论指导,利用自主搭建的双光子纠缠源制备光子纠缠态,通过测量不同条件下符合对比度计算Bell不等式,验证了量子力学的完备性.

量子力学完备性;Bell不等式破缺;CHSH不等式;纠缠源

1 引 言

量子力学与相对论是近代物理学的两大基础理论.量子力学是上世纪20年代创立的描述微观世界物质运动规律的一门科学.正统量子力学物理诠释主要内容是波函数的概率解释[1]、不确定原理[2]和Bohr提出的互补原理[3].然而,在量子力学概率诠释提出之初,就遭到了Einstein的批评与责难,引发了一场论战.Einstein认为以概率诠释为基础的量子力学理论是不完备的.从1927年到1955年Einstein逝世,Bohr和Einstein多次对量子力学完备性问题进行激烈的辩论,最终他们谁也没有说服对方.此后,关于量子力学物理诠释的争论仍在继续,并一直延续至今. Einstein之后,在这一场争论中发生的最重要的事件是“隐变量理论”[4]和“Bell不等式”[5]的提出.1965年,Bell在局域隐变量理论的基础上导出一个不等式,称为“Bell不等式”.此不等式与量子力学的预言不相符,于是可以通过对此不等式的实验检验来判断正统量子力学的概率诠释是否正确.

我们的实验正是以Bell不等式的推广形式CHSH不等式[6]为理论指导,应用双光子纠缠源技术实现对量子力学完备性的验证.本文所涉及的实验内容已作为清华大学近代物理实验室量子纠缠实验[7]的子题目,用于为高年级本科生和部分研究生开设研究型教学实验课程.希望通过这样的实验内容,让学生在基础实验课程阶段就有机会感受量子力学的神奇和魅力,从而激发学生的学习兴趣,鼓励学生的创新精神.

2 量子纠缠态与量子力学完备性

光子纠缠源是量子纠缠的一种技术实现手段,借助光子纠缠源,通过对以特定方法制备的偏振纠缠光子对的统计计数,可以获得相关数据,加以分析后可以了解量子纠缠的性质,体现量子力学的规律.

量子纠缠是指多个量子系统之间存在的非定域、非经典的强关联,它描述了子系统间不可分离的特性[7].在实验系统中,关联性体现在成对的2个光子之间始终保持着相互垂直的偏振关系;“非定域、非经典”和不可分离性则体现在,2个光子之中的任何一个的偏振无法孤立地得到测量,而不对另一个光子产生影响.事实上,在测量过程中,对一个光子的测量,导致了另一个与之成对的光子状态发生坍缩,而偏振关系相互垂直的关联性恰恰体现于其中.

1935年Einstein,Podohsky和Rosen联名发表文章,首次对量子力学完备性予以质疑,提出了著名的“EPR佯谬”[8].通过精妙的假想实验和逻辑推理,Einstein等人得出以下二者必居其一的结论:

1)存在着瞬时的超距作用,在测量粒子1的同时,立即干扰了粒子2的对应物理量;

2)一些物理量本来可以同时有精确值,只是量子力学的描述不完备.

在其后的30年当中,量子力学完备与否的争论在学术界广泛展开起来,直到1965年,Bell在局域隐变量理论的基础上推导出“Bell不等式”[5].此不等式与量子力学的预言不相符,于是就有可能通过对此不等式的实验检验来判断正统量子力学的诠释是否正确,进而判断量子力学完备与否.

实验上容易检验的“Bell不等式”形式是1969年Clauser,Horne,Shimony和Holt提出的CHSH不等式[6]:

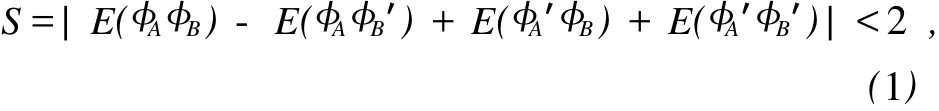
其中

NφAφA为AB两路偏振片分别为φA和φB时的符合计数.该不等式将成为以下实验数据处理的指导数学形式.

3 实 验

产生纠缠光子对的基本实验装置示意图如图1所示.实验过程参见文献[7].表1列出与实验最终数据密切相关的仪器设备参量.单模光纤准直器15和16与主BBO晶体5之间的接收距离为400～425 mm.

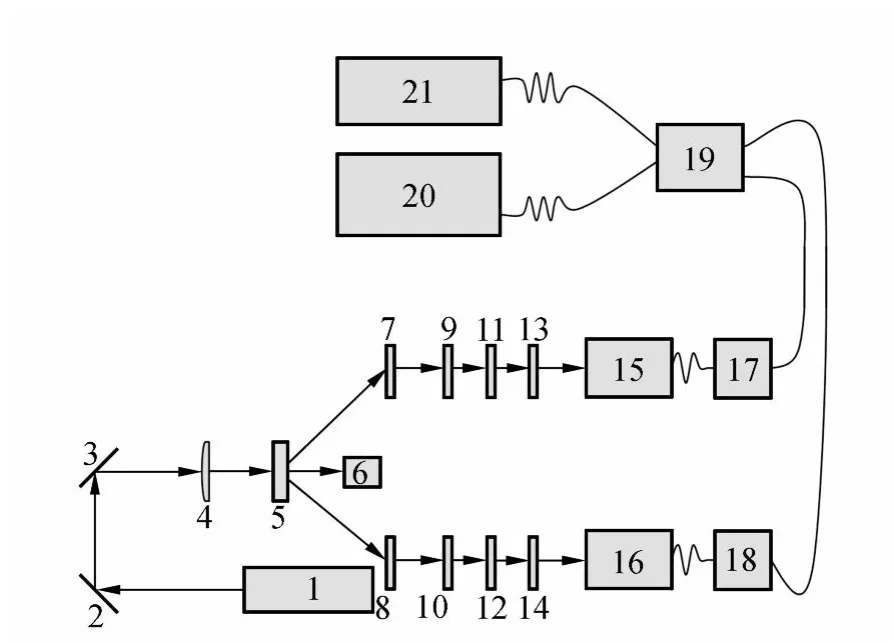
图1 应用双光子纠缠验证量子力学完备性的实验装置示意图

表1 仪器设备及参量

实验过程中标记探测器17所计数据为A路数据,探测器18所计数据为B路数据,电子学模块符合宽度设置为3 ns.标记偏振片通光方向水平为H,竖直为V,与竖直向上呈右旋45°为+,呈左旋45°为-.定义实验过程中A和B路偏振片分别取H和V时的符合计数值与分别取H和H时的符合计数值之比为H/V对比度;A和B路偏振片分别取+和-时的符合计数值与分别取+和+时的符合计数值之比为+/-对比度.

调节光路得单路计数:A路为58 820 s-1,B路为68 999 s-1,总符合数为7 051 s-1;H/V对比度约为72∶1,+/-对比度约为15∶1时,开始进行数据采集.

4 结果与讨论

4.1 光子纠缠态制备

光路调好之后,首先测量A,B两路光子的对比度曲线,以判断两路光子是否为纠缠态.符合测量时将A路偏振片分别放置于H和-位置,旋转B路偏振片进行测量.

条件Ⅰ:入射光从补偿BBO晶体中心通过(中心比较模糊,透过率较低),测量符合曲线如图2所示.

条件Ⅱ:入射光从补偿BBO晶体边缘通过(边缘相对干净,透过率较高),测量符合曲线如图3所示.

从图2～3(图中横坐标为偏振片角度,纵坐标为两路光子符合计数)可以看出所采集数据形成了明显的峰谷曲线趋势,由曲线可以观察到,峰谷位置相差为90°.这一结果体现了两路光子偏振方向之间的相互垂直关系,从而体现了反关联属性,说明两路光子具有偏振纠缠特性,也即完成双光子纠缠态的制备.

图2 条件Ⅰ下符合数据曲线

图3 条件Ⅱ下符合数据曲线

4.2 符合对比度与Bell不等式破缺验证

量子纠缠态应遵守量子力学的基本原理,用它们测量计算的Bell不等式应符合量子力学的结论.分别用上述方法制备的纠缠光子对做2种不同条件下符合对比度测量,并且计算Bell不等式,符合计数统计测试时间为10 s,结果如表2～7所示.

表2 在条件Ⅰ时,2种基矢下符合对比度测量结果

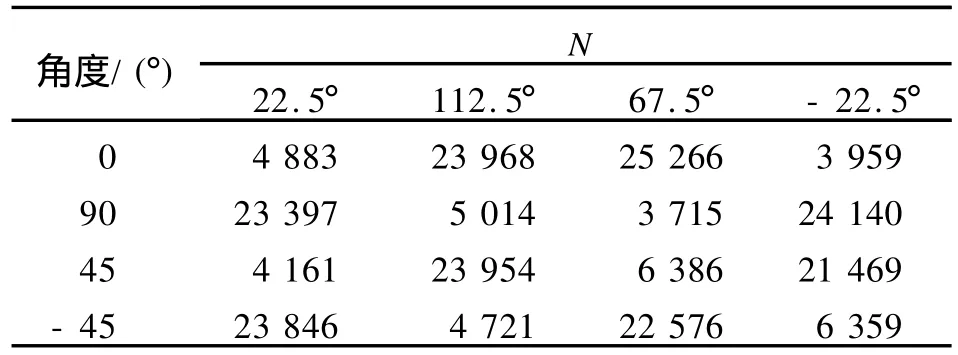
表3 在条件Ⅰ时,Bell不等式破缺测量

将表2～3符合计数统计数据代入式(2)中计算得到对应不同角度下E值及其偏差见表4.

表4 条件I时不同角度下E值及其偏差

再将表3中的E值与偏差数据代入式(1)中计算,得Bell不等式破缺测试结果:S1=2.623± 0.006,99.7个标准偏差破坏Bell不等式.

综合以上数据计算结果,由量子力学完备性原理部分的CHSH不等式,定域实在论认为S≤2,量子力学认为S≤22,实验所得S1= 2.623±0.006>2,与量子力学理论的结果相符合,从而在实验上验证Bell不等式的破缺,支持了量子力学的结论,验证了量子力学完备性.

在条件Ⅱ时,依同样方法测得2种基矢下符合对比度,Bell不等式破缺测量及对应E值与偏差结果如表5～7所示.

表5 在条件Ⅱ时,2种基矢下符合对比度测量结果

表6 在条件Ⅱ时,Bell不等式破缺测量

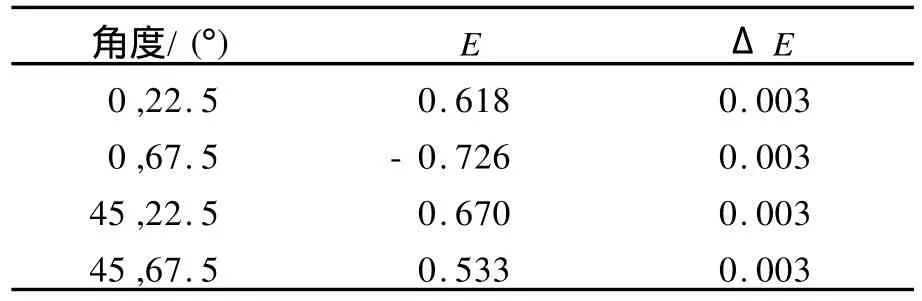
表7 条件Ⅱ时不同角度下E值及其偏差

Bell不等式破缺测试结果:S2=2.546± 0.005,99.3个标准偏差破坏Bell不等式.

此实验数据结果,S2=2.546±0.005>2,仍然支持量子力学的结论.

由2种条件下所得数据进行对比,可以了解到:第1组的计数记录值普遍小于第2组,而对比度普遍优于第2组;从破缺结果看到S1= 2.623±0.006,99.7个标准偏差破坏Bell不等式,S2=2.546±0.005,99.3个标准偏差破坏Bell不等式,说明这一实验的成败关键在于2种基矢条件下符合对比度的大小,而与计数记录值的大小无直接关系.由此得出实验中的数据核心与操作判据为符合对比度的大小.

5 结束语

本实验以纠缠源为实验对象,以验证量子力学完备性为实验目标.将量子力学基本原理体现于基础实验教学之中,在实验教学的各个环节中都发挥了积极与良好的作用[7].在更深层次, Einstein与Bohr之争在很大程度上是哲学观点之争[9],学生可以通过对物理学界关于量子力学自洽性和完备性的争论历史的了解,感受到从事物理学研究工作也应以辩证唯物主义为指导,贯彻“实践是检验真理的唯一标准”这一基本原理.

[1] Born M.Zur quantenmechanik der stossvorgange [J].Z.Physik,1926,37:863-867.

[2] Heisenberg W.Uber den anschaulichen inhalt der quantentheoretischen kinematik and mechanik[J]. Z.Physik,1927,43:172-198.

[3] Bohr N.Atomic theory and the description of nature[M].London:Cambridge University Press, 1934:52-91.

[4] Bohm D.A suggested interpretation of the quantum theory in terms of“hidden”variables,I andⅡ[J]. Phys.Rev.,1952,85(2):166-179,180-193.

[5] Bell J S.Speakable and unspeakable in quantum mechanics[M].London:CambridgeUniversity Press,1987.

[6] Clauser J F,Horne M A,Shimony A,et al.Proposed experiment to test local hidden-variable theories[J].Phys.Rev.Lett.,1969,23:880-884.

[7] 王合英,孙文博.光量子纠缠态的制备和测量实验[J].物理实验,2009,29(3):1-5.

[8] Einstein A,Podolsky B,Rosen N.Can quantummechanical description of realiy be considered complete?[J].Phys.Rev.,1935,47:777-780.

[9] 雅默M.量子力学的哲学[M].秦克诚译.北京:商务印书馆,1989:126-152,154-158,225-229,292-295.

Experimental verification of the Bell inequality using two-photon entanglement source

SUN Wen-bo,WANG He-ying,CHEN Yi-bao,HE Yuan-jin
(Department of Physics,Tsinghua University,Beijing 100084,China)

Entanglement is prepared based on the CHSH inequality,the extended form of Bell inequality and a self-made system of two-photon entanglement source.The Bell inequality is calculated by measuring the coincidence contrast in different conditions.Thus the completeness of quantum mechanics is verified.

completeness of quantum mechanics;Bell inequality;CHSH inequality;entanglement source

O413.1

A

1005-4642(2010)12-0001-04

[责任编辑:任德香]

“第6届全国高等学校物理实验教学研讨会”论文

2010-06-18;修改日期:2010-09-06

孙文博(1980-),男,辽宁锦州人,清华大学物理系工程师,学士,从事近代物理实验教学工作.