双钙钛矿氧化物Sr2FeMoO6的结构特征及磁性质

杨小兰，高钦翔，万 猛

(遵义师范学院物理系,贵州遵义563002)

双钙钛矿氧化物Sr2FeMoO6的结构特征及磁性质

杨小兰，高钦翔，万 猛

(遵义师范学院物理系,贵州遵义563002)

与钙钛矿ABO3型氧化物材料进行比较，阐述了双钙钛矿A2BB'O6型氧化物材料的某些电磁特性及掺杂效应。

双钙钛矿氧化物；结构；磁电阻效应

1998年，Kobayashi等人曾报道：在室温低场下，双钙钛矿型氧化物Sr2FeMoO6具有高达10%的隧穿型磁电阻效应[1]，此后，这类氧化物备受关注。本文从双钙钛矿氧化物的结构特点出发，阐述了其某些电磁特性及掺杂效应。

1 双钙钛矿氧化物的结构特点

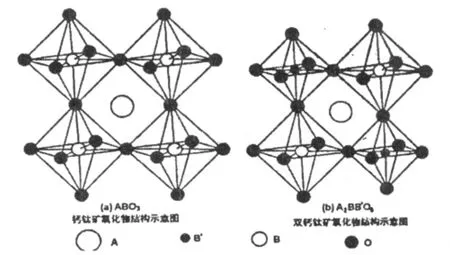
图1 (a)ABO3型钙钛矿氧化物的结构示意图(b)A2BB'O6型双钙钛矿氧化物的结构示意图

双钙钛矿A2BB'O6型氧化物是相应于钙钛矿ABO3型氧化物而命名的。图1(a)为ABO3型钙钛矿氧化物的结构示意图,A为离子半径大的稀土类元素或碱土金属等，B为离子半径小的过渡金属元素等，B离子位于由氧离子围成的八面体的体心。图1(b)为A2BB'O6型双钙钛矿氧化物的结构示意图，B位原子的八面体结构由BO6和B'O6交替排列而成，各个B、B'离子被氧离子隔开形成B-O-B'结合。此时，B-O-B'的180°超交换作用占主导地位，可以忽略直接交换作用和90°超交换作用的影响。但实际上离子大小、离子间的相互作用会对结构产生影响，多数情况会发生畸变，比如，在A2FeMoO6中，若A依次为Ca、Sr、Ba时，其晶体结构也依次由单斜到四方再到立方。

理想的双钙钛矿氧化物Sr2FeMoO6属四方晶系,I4/m空间群。图2为我们根据实验数据，选择晶格参数a=b=0.5571 nm,c=0.7902 nm,α=β=γ=90°[2]来建立的晶体结构图。

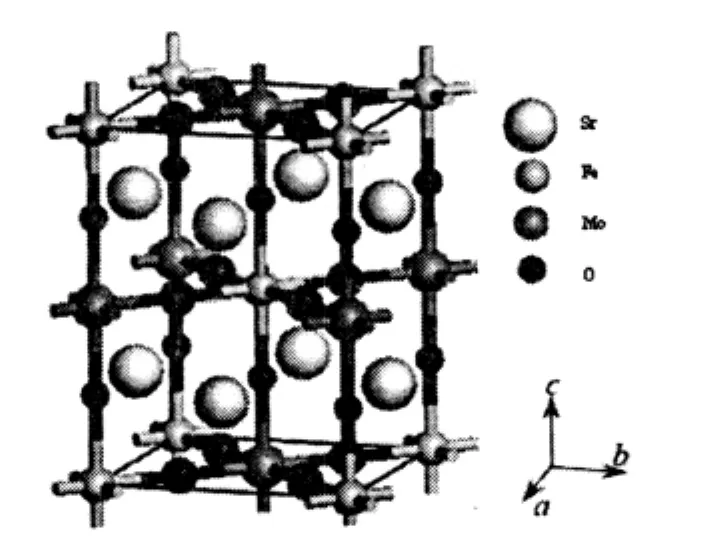
图2 Sr2FeMoO6的结构模型

2 双钙钛矿氧化物的电磁特性

能带计算发现具有室温磁电阻效应的双钙钛矿氧化物一般都具有半金属性。这里半金属性的概念是Groot等人在1983年提出来的，他们在对锰基semi-Heusler合金NiMnSb和PtMnSb作能带结构计算时，得到了一种特殊的能带结构，这些磁性金属化合物与一切普通的铁磁体一样，具有两个不同的自旋子能带，但有趣的是，其中一个自旋子能带在费米面上有传导电子，而对于另一个子能带，费米能级恰好落在价带与导带之间的能隙中。这种半金属在宏观上通常表现为具有金属性的磁性化合物，但是在晶体结构、键的性质以及较大的交换劈裂等因素的共同影响下，其能隙恰好只在一个自旋方向的子能带中打开，从而实现了金属性与绝缘性在微观尺度下的共存。因而，半金属性的一个特征就是整数磁矩，即所谓的“磁矩量子化”现象。在半金属化合物中，如果自旋向下的子能带被占满，平均每个原胞容纳的自旋向下的电子数密度n-必为整数值，于是在另一个子能带中容纳的自旋向上的电子数密度n+＝n-n-(n为原胞中的价电子总数)也是一个整数，最终导致平均磁矩m＝(n+-n-)μB为玻尔磁矩μB的整数倍。

半金属性具有的这样一种特殊的能带结构自然会带来一系列特殊的性质，其中最显著的表现是传导电子的完全自旋极化。如前所述，半金属只有一个自旋子能带在费米面上有传导电子分布，因而所有的传导电子都具有相同的自旋方向，根据自旋极化率P的一般定义，P＝[N↑(E)-N↓(E)]/[N↑(E)+N↓(E)]，其中Nα(E)是能级E上自旋为α的电子态密度(α＝↑,↓)。因此，半金属在费米能级上的电子自旋极化率为百分之百(P＝±100%)，远远超过了一般铁磁金属及其合金的极化率范围(P＝10%～40%)。对于双层钙钛矿型氧化物Sr2FeMoO6而言,自旋向下子能带在费米面上有传导电子，而对于自旋向上子能带，费米能级恰好落在其价带与导带之间的能隙中，所以，在费米能级上的电子自旋极化率为负的百分之百(P＝-100%)。根据Julliere理论，磁电阻的大小和传导电子的自旋极化率成正比，那么传导电子的完全自旋极化是双层钙钛矿型氧化物具有室温磁电阻的内禀原因。通过上述分析可知，具有半金属性的材料就具有强烈的自旋劈裂特性，从而磁场就对它们的导电性能有很大的影响，这样就具备了产生磁电阻效应的条件。

钙钛矿型氧化物的巨磁电阻效应（CMR）的发现，极大的推动自旋极化输运现象和磁电子学的研究，这方面的研究有助于凝聚态物理学的发展。因而，双钙钛矿氧化物的应用价值非常广，尤其是在磁记录、磁传感器以及开关元器件等方面具有潜在的应用前景。

3 A位或B位离子掺杂对双钙钛矿型氧化物Sr2 FeMoO6 电磁性质的影响

对双钙钛矿型氧化物Sr2FeMoO6,BO6八面体及其周围环境的改变都将影响材料的电、磁特性,因此,我们可以通过Sr位掺杂改变A位离子半径 ＜rA＞,进而改变BO6八面体周围的环境,来研究其对电磁特性的影响;也可以通过B位 (即Fe位或Mo位)掺杂,掺杂元素直接作用于八面体本身,改变Fe-O-Mo之间的交换作用,进而对其掺杂系统的电磁特性展开研究。

3.1 实验研究

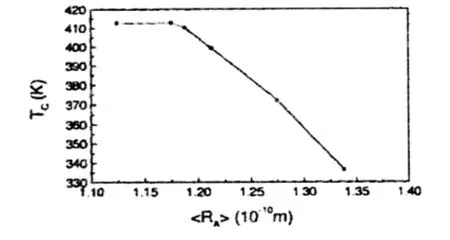
图3 A2FeMoO6系统居里温度随A位平均离子半径的变化关系

图3为A2FeMoO6系统居里温度随A位平均离子半径的变化关系。Patterson和Galasso研究表明，居里温度TC随着A位离子半径的减小而增加，即A位离子半径的减小将导致B-O-B'键长的缩短,从而有利于B-O-B'超交换作用。当A位由大的Sr2+离子变为小的Ca2+离子时，居里温度反而下降，这是因为在这些化合物中比较小的Ca2+离子会造成较大的晶体结构畸变，使得O-B-O或O-B'-O的键角偏离180°，不利于超交换作用，从而影响磁交换作用，致使居里温度下降。也就是说，在这些化合物中，与键长变化相比较,键角的变化对磁相互作用的影响更大。Galasso等人认为A2FeMoO6系列氧化物则正好反映了键长、键角对磁相互作用的共同影响。从Ba2FeMoO6到Sr2FeMoO6，键长起主要作用，而从Sr2FeMoO6到Ca2FeMoO6，键角起主要作用。

B位掺杂对双钙钛矿型氧化物Sr2FeMoO6电、磁特性的影响:

近期多个实验都报道了在Fe位掺杂Cr离子对Sr2FeMoO6磁学和输运性质的影响,发现Cr掺杂降低了Sr2FeMoO6的阳离子有序、饱和磁化强度和磁电阻效应[3,4]。Fe位非磁性Al3+离子的掺杂会产生许多无磁相互作用的Mo-O-Al-O-Mo,可以将亚铁磁区域分割成许多更小的区域，从而显著地提高了低场磁电阻效应[5]。同时，Al的掺杂会抑制反铁磁Fe-O-Fe的形成，提高了阳离子的有序度，因此提高了平均单位Fe离子的磁矩并降低了高场磁电阻。

实验结果显示，在Sr2Fe1-xCoxMoO6体系中，随着Co替代浓度x值的增加，系统由半金属变为半导体，样品也由亚铁磁体转变为反铁磁体，其磁相变温度也随之下降，Co对Fe的部分替代抑制了该体系的磁电阻效应。在Sr2(Fe1-xMnx)MoO6(0≤x≤0.45)体系中，饱和磁化强度、居里温度以及磁电阻效应由于Mn掺杂而显著降低[6]。根据所提出的相分离模型得出：（Mn3+，Mo5+）和（Mn2+，Mo6+）价态对同时存在，Mn3+替代Fe3+有一饱和值，当掺杂含量大于一定值时，Mn离子多以+2价形式出现。运用逾渗机理对实验的电阻及磁电阻结果进行了很好的解释。当掺杂量大于一定的临界浓度时，孤立的绝缘反铁磁团簇Sr2Mn－MoO6开始彼此连接形成反铁磁区域，使得电阻率陡升，同时这可能也是出现正磁电阻现象的原因所在。

Fe位Cu的掺杂降低了低场磁电阻效应，掺杂越多降低得就越明显。磁电阻随掺杂的增加而缓慢降低，磁电阻对温度的依赖关系随掺杂的增加没有明显的改变。磁电阻随掺杂变化的极小值出现在20%处，这可能是与在掺杂为15%以后发生了金属一半导体的转变有关。因为Cu没有磁矩，分子饱和磁矩随掺杂的增加而降低，同时平均单位Fe离子的磁矩也随着下降。Fe位Zn掺杂使得Zn离子进入Sr2FeMoO6晶格替代Fe离子后，一方面，Zn的掺杂打破了Fe、Mo有序使O-Fe-O-Mo-O反铁磁耦合作用变弱;另一方面，将样品内部结构有序的较大的亚铁磁区分割为更多的小亚铁磁区,小亚铁磁区的磁化方向更容易在低场下平行排列。这两方面的共同作用显著增强了材料的低场磁电阻效应，也导致了高场磁电阻的减小[2]。但是掺杂导致的磁相互作用变弱使样品的磁化方向在高温时更容易受到热扰动的影响，从而使得样品的低场磁电阻效应和饱和磁矩表现出更强的温度依赖性。非磁性的Zn掺杂降低了材料的有序度，从而降低了材料的饱和磁矩和居里温度[7]。

为进一步找到具有更高室温磁电阻效应的材料,可以用3d位电子对其性质起主导作用的过渡族金属元素的不同组合作为B位的候选对象来构成双钙钛矿材料,并辅以适当的理论手段:比如能带计算来加以选择,将是一种较为迅捷的方法。这是由于,3d电子、p-d电子间(P电子由氧原子提供)的相互作用会使这类氧化物更易具有自旋分裂的特性。

3.2 理论计算

计算工作是由基于密度泛函理论 (DFT)的CASTEP量子力学模块完成的。密度泛函理论的基本想法是原子、分子和固体的基态物理性质可以用粒子密度函数来描述，这一思想起源H.Thomas和E.Femi的工作。20世纪60年代，Hohenberg,Kohn和Sham（沈吕九）提出了密度泛函理论，简称DFT。这个理论不但建立了将多电子问题化为单电子方程的理论基础，同时也给出了单电子有效势如何计算的理论依据。Hohenberg-Kohn第一定理说明多粒子体系的基态单粒子密度与其所处的外势场之间有一一对应关系，同时确定了体系的粒子数，从而决定了体系的哈密顿算符，进而决定体系的所有性质。这条定理为密度泛函理论打下坚实的理论基础。第二定理是密度泛函框架下的变分原理，即体系基态总能量（表示成粒子密度的泛函形式）在体系基态单粒子密度处取极小值，即为体系的基态真实总能量。Kohn和Sham提出了用无相互作用参考体系的动能来估计实际体系动能的主要部分，把动能的误差部分和相互作用能与库仑作用能之差归并为一项,再寻求其近似形式,这就是所谓的Kohn-Sham方法。

在密度泛函理论中，局域密度近似（LDA）是一个普遍使用的相对简单且简化的近似方法，然而它在预测晶体材料的机械结构（如晶格常数a,b,c,d,g）及能带结构上却有出乎意料之外的成功。后来学者专家探讨其原因，归纳出一些理由，最重要的是，虽然它是很大的近似，但它仍然满足某些交换相干能在原理上就原本应该具有的重要的总数规则（Sum Rule）。但严格地说局域密度近似只适用于密度足够缓慢变化或者高密度情况，对于一般的密度变化并不缓慢体系的描述，理论上并不清楚。在计算上，人们对局域密度近似进行了改进和修正，比如自相互作用修正（SIC）、自能修正（SEC或GWA）、以及广义的梯度近似（GGA）。在CASTEP里预设的是GGA，在很多状况下它被认为是比较好的方法。有许多证据显示GGA会在离子晶体过度修正LDA结果；当LDA与实验符合得非常好的时候，GGA会高估晶格长度。

在Hohenberg-Kohn-Sham方程的框架下，对固体的电子结构计算，可以将其多电子系统的基态特性问题在形式上转化成有效单电子问题。然而这只有在找出了交换关联势能泛函准确且便于表达的形式时才有实际意义，没有其具体形式无法展开实际计算。因此，交换关联泛函在密度泛函理论中占有重要地位。

CASTEP是特别为固体材料学而设计的一个现代的量子力学基本程序，该软件提供了友好的用户界面，广泛地应用于材料的计算机模拟计算。它有机地结合了密度泛函理论（DFT）和分子动力学（MD）技术，是目前材料设计和计算机模拟实验中最先进、最重要的赝势能带方法之一。基于密度泛函平面波赝势方法的CASTEP软件可以对许多体系包括像半导体、陶瓷、金属、矿石、沸石等材料进行第一原理量子力学计算。半导体和其他固体材料的许多性能由电子性质决定，而电子性质又由原子结构决定，特别是缺陷在改变电子结构上的作用对半导体性质尤为重要。分子模拟，特别是量子物理技术，可用来预测原子和电子结构及分析缺陷对材料性能的影响。CASTEP能有效的研究存在点缺陷、空位、替代杂质、位错等的半导体和其它材料中的的性能。CASTEP的量子力学方法，为深入了解固体材料的这些性质并进而设计新的材料，提供了强有力的工具。

CASTEP软件典型的功能包括研究表面化学、能带结构、态密度、和光学性质。它也能够研究体系电荷密度的空间分布和体系波函数。CASTEP还可以用来计算晶体的弹性模量和相关的机械性能，如泊松系数等。总的来说，它可以实现：计算体系的总能；进行结构优化；执行动力学任务；在设置的温度和关联参数下，研究体系中原子的运动行为；化学反应的过度态搜索等。除此之外，计算一些晶体的性质，如能带结构、态密度、聚居数分析、声子色散关系、声子态密度、光学性质、应力等。量子力学计算精确度高但计算密集，直到最近，表征固体和表面所需的扩展体系的量子力学模拟对大多数研究者来说才切实可行。然而，不断发展的计算机功能和算法的进步使这种计算越来越容易实现，与许多该领域一流专家一起工作推动固体量子力学发展，通过提供可以方便直接进入上述CASTEP计算方法中。

CASTEP软件的使用包括计算任务的设置、计算体系性质的设置和计算结果的分析。计算任务的设置，主要是通过Visualizer应用窗口中的工具条之一“Calculation”来进行。我们可以更改工具框中的相应选项，来配置诸如：“电子选项”,“结构优化选项”和“电子和结构性质选项”等。这几个选项是我们在运用CASTEP计算研究中非常重要的几个技术参数。在程序运行之前，从研究的问题出发，要将软件中关键的一些任务参数设置成符合计算需要的值，我们才能得到所期望的运算结果。计算结果的分析，能带计算完成后，进行操作，则在Visualizer界面中会显示能带和对应的总的态密度图，得到的能带和总的密度图还可以导出到如origin软件中进行处理,以利于更直观的分析。

结合实验分析,我们采用密度泛函理论 (DFT)下的平面波赝势 (PWP)法和广义梯度近似(GGA),对Sr2Fe1-xCrxMoO6、Ba2-xSrxFeMoO6等体系进行了理论计算,首先通过几何结构优化,得到体系的晶格参数,并在优化基础上计算和分析了体系的能带结构、总体态密度、分波态密度及A位、B位掺杂对Sr2FeMoO6电磁特性的影响。计算结果显示，Fe位Cr掺杂使体系Fe-O键长减小,Cr-O、Mo-O键长增加,Fe-O-Mo、Cr-O-Mo键角逐渐趋近于 180°,晶格常数和晶胞体积逐渐减小，降低了体系总磁矩及Fe离子磁矩。对于Sr2Fe1-xCrxMoO6体系，当x=0,1/3时,自旋向上子能带的能隙分别为1.25、1.21 eV,自旋向下子能带跨过费米面,具有半金属性特征；当x=0.5时,自旋向上、向下的子能带都跨过费米面,呈现出金属性；当x=1时,Sr2CrMoO6具有半金属性。对于 Ba2-xSrxFeMoO6体系，Sr掺杂使 Fe-O，Sr-O，Mo-O键长减小，晶格常数和晶胞体积略有减小；Sr掺杂减小了体系总磁矩；当x=0,1,2时,自旋向上子能带的能隙分别为1.08、0.90、1.25 eV,自旋向下子能带跨过费米面,都具有半金属性特征。

4 结束语

双钙钛矿A2BB'O6型氧化物无论是在实用方面,还是在理论方面,都具有相当大的研究价值。这类氧化物由于B、B′位离子具有不同的离子半径、不同的电子组态以及相互间不同类型的交换作用,可以通过改变它们的组合来探究多种不同类型的问题。

[1]Koba Yashi K I,Klmura T,Sawada H,et al.Room-temperature magnetoresistance in an oxide material with an ordered doubleperovskite structure[J].Nature,1998,395(15):677-680.

[2]Min Feng Lü,Jing Ping Wang,Jian Fen Liu,Wei Song,Xian Feng Hao,De Feng Zhou,Xiao Juan Liu,Zhi Jian Wu and Jian Meng.An investigation of low-field magnetoresistance in the double perovskites Sr2Fe11-xZnxMoO6,x=0,0.05,0.15 and 0.25[J].Journal of Physics:Condensed Matter,2006,18(1):1601-1612.

[3]Je Hoon Kim,Geun Young Ahn,Seung-Iel Park,Chul Sung Kim.Effects of Cr doping on magnetic properties of ordered Sr2FeMoO6[J].Journal of Magnetism and Magnetic Materials,2004,282(1):295-298.

[4]J.Bashira,R.Shaheena,M.Siddiquea,A.K.Azadb,J.Eriksenb,H.Rundlöf.The influence of Cr doping on the structural and magnetic properties of Sr2Fe1-xCrxMoO6double perovskite[J].Physica B:Condensed Matter,2006,385(1):126-129.

[5]Y.Sui,X.J.Wang,Z.N.Qian,Z.G.Liu,J.P.Miao,J.G.Cheng,X.Q.Huang,Z.Lu,W.H.Su,C.K.Ong.Influence of doping Alon the magnetoresistance ofpolycrystalline Sr2FeMoO6[J].Journal of Magnetism and Magnetic Materials,2005,290(1):1089-1092.

[6]Asok Poddar,Chandan Mazumdar.Spin glass-like behaviour in Fe-rich phases of Sr2Fe1-xMnxMoO6(0.1≤x≤0.4)[J].Journal of Alloys and Compounds,2010,502(1):13-15.

[7]Xianjie Wang,Yu Sui,Qiuli Yang,Jinguang Cheng,Zhengnan Qian,Zhiguo Liu,Wenhui Su.Effect of doping Zn on the magnetoresistance of polycrystalline Sr2FeMoO6[J].Journal of Alloys and Compounds,2007,431(1):6-9.

（责任编辑：朱 彬）

Structural and Magnetic Properties of Double Perovskite Sr2FeMoO6

YANG Xiao-lan，GAO Qin-xiang,WAN Meng
(Department of Physics,Zunyi Normal College,Zunyi 563002,China)

On the basis of comparison with perovskite(ABO3)materials,and in terms of theory and experiment,this paper endeavors to look at some electro-magnetism properties and doping effect of oxides materials of double-perovskite(A2BB'O6).

double perovskite;structure;Magnetoresistance effect

O441

A

1009-3583（2010）-04－0079-04

2010-05-14

遵义师范学院重点学科建设项目（理论物理）（院科字185（11）号）

杨小兰，女，重庆人，遵义师范学院物理系教师，硕士，主要研究方向：凝聚态理论与计算凝聚态物理。