一种基于信息增益的蚁群聚类算法
2010-09-20罗聪曹三省杜怀昌
罗聪,曹三省,2,杜怀昌
(1.中国传媒大学信息工程学院,北京 100024;2.南京大学计算机软件新技术国家重点实验室,南京 210093)
1 引言
受生物进化机理的启发,科学家提出了许多用以解决复杂优化问题的新方法,如遗传算法、进化策略等。1991年意大利学者 Dorigo M等提出了蚁群算法。它是一种新型的优化方法。该算法不依赖于具体问题的数学描述,具有全局优化能力。后来其它科学家根据自然界真实蚂蚁堆积尸体及分工行为,提出了基于蚂蚁的聚类算法。利用简单的智能体模仿蚂蚁在给定的环境中随意移动。这些算法的基本原理简单,已经应用到电路设计、文本挖掘等领域。蚁群算法作为一种模拟进化算法,具有如下的特征:(1)蚁群算法是一种自组织的算法;(2)蚁群算法是一种本质上并行的算法;(3)蚁群算法是一种正反馈的算法;(4)蚁群算法具有较强的鲁棒性;(5)蚁群算法是一种通用型随机优化方法;(6)蚁群算法是一种启发式算法。
但是,蚁群聚类算法有两个明显的缺点:(1)由于输入数据的所有属性均等地参与计算,没有突出属性的重要程度,聚类结果可能发生较大的偏差;(2)对于大量的数据,如果数据的维数过高,算法将运行很长的时间,使算法的时间效率非常低。
针对上述缺点,本文利用信息增益来衡量属性的重要程度,选择信息增益较大的属性实现数据的降维,既解决了属性均等重要的问题,又降低了计算量,大大缩短了算法的运行时间。
2 基本蚁群算法的原理
蚁群系统是最早建立的蚁群算法模型,其模型的建立来源于对蚂蚁寻找食物行为的研究。在自然界中,只要仔细观察就可以发现,蚂蚁总能找到一条从蚁巢到食物源的最短路径。尽管单只蚂蚁的能力和智力非常简单,但蚁群却表现出极其复杂的行为特征,在许多情况下能完成远远超过蚂蚁个体能力的复杂任务。蚁群的这种能力来源于蚂蚁群体中的个体协作行为,通过研究发现,蚂蚁个体之间是通过一种称之为信息素(pheromone)的挥发性的化学物质进行信息传递,从而能相互协作,完成复杂的任务。蚁群表现出复杂有序的行为,个体之间的信息交流与相互协作起着重要的作用。觅食的蚂蚁寻找食物时,当碰到一个还没有走过的路口时,就随机地挑选一条路径前行,在其走过的路径上留下与路径长度相关的信息素,而且能够感知这种物质的存在及其强度,并以此指导自己的运动方向,蚂蚁倾向于信息素浓度高的方向移动。因此,由大量蚂蚁组成的蚁群的集体行为便表现出一种信息正反馈现象,即某一路径上走过的蚂蚁越多,则后来者选择该路径的概率就越大。蚂蚁个体之间就是通过这种信息交流机制来寻找食物,并最终沿着最短路径行进。
3 蚁群聚类算法的设计与实现
本文设计的蚁群聚类算法是基于蚁堆原理的,基于蚁堆原理的聚类方法的灵感来源于自然界中蚂蚁分类其尸体和幼体的方法。蚁群聚类算法设计的基本思想是将待处理的多维数据随机的分布在一个二维平面上,然后在二维平面上引入一些人工蚂蚁,人工蚂蚁在二维平面上随机移动,根据其在某地点发现的数据对象在局部区域的相似性而得到的概率决定该蚂蚁是否拾起、放下该数据对象。经过有限次的迭代,平面上的数据按其相似性而聚集。
在数据分析中,比较典型的情况是待处理数据对象是由有限取值的 n维属性定义的,也就是 Rn空间中的点,此时,d(i,j)表示了这些对象间的距离,这里 d(i,j)的定义采用了欧几里德距离,即:

假设d(Oi,Oj)为属性空间中数据对象 Oi和 Oj间的距离,t时刻蚂蚁在位置 p处,且物体 Oi就在当前位置。与物体 Oi相关的局部密度 f(Oi)定义如下:
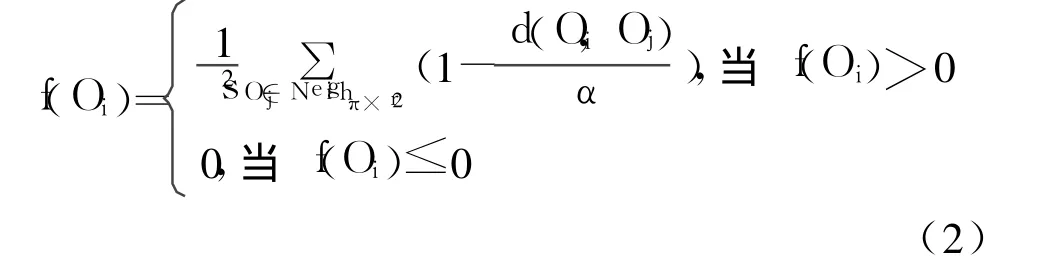
f(Oi)是 Oi与相邻的其它数据对象的相似性度量,称作平均相似度函数。r是蚂蚁的搜索半径,即蚂蚁在平面移动过程中可直接观察到以当前位置 p为圆心,以 r为半径的区域范围内的物体分布情况。α是差异性比例因子,利用它可以决定两个物体是否可放置在一起。如果 α较大,则不同物体之间的区分度不明显,导致形成的簇覆盖过宽,同簇中物体不一定具备相近属性。反之,如果 α过小,则会导致物体间差异度量被放大,从而使得原本相似属性的数据不能够聚合到一簇中。当 f(Oi)接近于 0时,Oi被拾起的概率比较大,反之 f(Oi)接近于 1时,被拾起的概率比较小。这样就可以对蚂蚁拾起或放下物体的概率选择方式定义如下:

其中 k1,k2都是阈值常量。
算法模型基本流程设计如下:
第 1步 初始化差异性比例因子、拾起和放下概率参数、最大迭代次数等算法模型参数;
第 2步 随机投射数据对象到一个二维平面,即随机赋给每个数据对象一对坐标(x,y);
第 3步 初始化蚂蚁状态为无负载,并将蚂蚁随机投放到二维平面内一个被数据对象占据的位置;
第 4步 聚类开始,迭代次数加一;
第 5步 在蚂蚁搜索半径 r的范围内,利用公式(2)计算蚂蚁所选数据对象的平均相似度;
第 6步 在[0,1]区间生成一个随机数 R;
第 7步 如果蚂蚁无负载,利用第 5步运算结果计算拾起概率 Ppick,并跳到第 9步;
第 8步 如果蚂蚁有负载,利用第 5步运算结果计算放下概率 Pdrop,并跳到第 10步;
第 9步 比较 Ppick和 R的大小,如果 Ppick>R,蚂蚁拾起对象,并将蚂蚁标注有负载,跳到第 11步;否则跳到第 12步;
第 10步 比较 Pdrop和 R的大小,如果 Pdrop>R,蚂蚁放下对象,并将蚂蚁标注无负载,跳到第 12步;
第 11步 蚂蚁开始负载对象移动,将一个新的未被其他数据对象占据的随机坐标赋给蚂蚁,跳到第 13步;
第 12步 蚂蚁开始无负载移动,将一个新的被其他数据对象占据的随机坐标赋给蚂蚁;
第 13步 如果迭代次数小于在第 1步中设定的最大迭代次数,跳转到第 4步;否则进入第 14步;
第 14步 经过有限次迭代和收敛,平面上的数据对象按照其相似性而聚集,其中如果某个数据对象是孤立的或其邻域对象个数小于某一阈值,则标记该对象为孤立点;否则,给该数据对象分配一个聚类序列号,并将其邻域对象标记为同一序列号;
第 15步 输出聚类结果,算法结束。
4 基于信息增益的蚁群聚类算法的实验
4.1 实验数据处理过程
在本文中所采用的实验数据来自于五六四电台的 TSW2500型短波发射机秒数据。原始实验数据有 20个模拟量,维数过多,因此需要对数据进行预处理,使后面的处理过程可以有较高质量的输入数据,最终得到准确的聚类结果。数据处理过程如图1所示。
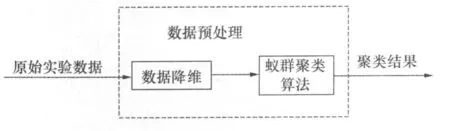
图 1 数据处理过程
高维数据对象的特征空间中含有许多冗余特征甚至噪声特征,这些特征一方面可能降低聚类的精度,另一方面会大大增加学习及训练的空间及时间复杂度,所以必须对原始实验数据进行数据降维。本文中采用计算属性的信息增益实现数据降维。
4.2 信息增益定义
令 X为随机变量,则 X的信息熵定义为:

通过观测随机变量 Y,随机变量 X的信息熵变为:

其中 P(xi)代表随机变量 X的先验概率,P(xi|yj)代表观测到随机变量 Y后随机变量 X的后验概率。引入随机变量 Y的信息后,随机变量 X的信息熵 H(X|Y)≤H(X),即引入 Y后,X的不确定程度会变小或保持不变。若 Y与 X不相关,则 H(X|Y)=H(X);若 Y与 X相关,则 H(X|Y)<H(X),而差值 H(X)-H(X|Y)越大,Y与 X的相关性越强。因此,式(7)定义信息增益 IG(X|Y)为 H(X)与 H(X|Y)的差值,反映了 Y与 X的相关程度,IG(X|Y)越大,则变量 Y与 X的相关性越强。
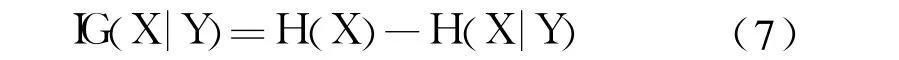
而且,可以证明,信息增益具有对称性,即 IG(X|Y)=IG(Y|X)。

表 1 发射机的示例训练样本数据表

(续表)

(续上右侧)

(续表)
4.3 基于信息增益的数据降维
表 1是发射机的示例训练样本数据表。首先,从表 1中选择“状态”属性作为标识属性,然后计算各属性的信息增益。根据“状态”属性的取值,将该训练样本数据表中的元组分为 2类,分别是状态“正常”和状态“故障”。状态“正常”类和状态“故障”类各包含 10个元组。
为了计算每一个属性的信息增益,首先计算“状态”属性的信息熵。

通过观测“反射功率”属性,“状态”属性的信息熵变为:

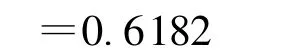
因此“反射功率”属性的信息增益是:

同理:“入射功率”的信息增益等于 0.7583;“宽放电流”的信息增益等于 0.5735;“宽放电压”的信息增益等于 0.0847;“高前阴流”的信息增益等于0.4552;“高前偏压”的信息增益等于 0.8623;“高前帘栅压”的信息增益等于 0.5049;“高前屏压”的信息增益等于 0.5573;“高前灯丝电流”的信息增益等于 0.3029;“高末屏流”的信息增益等于 0.7613;“高末偏压”的信息增益等于 0.4295;“高末帘栅压”的信息增益等于 0.9000;“高末屏压”的信息增益等于 0.8000;“高末灯丝电流”的信息增益等于0.5374;“高末栅流”的信息增益等于 0.2868;“高末帘栅流”的信息增益等于 0.6623;“冷凝器入水温度”的信息增益等于 0.5623;“冷凝器出水温度”的信息增益等于 0.2552;“实测频率”的信息增益等于0.6623;“驻波比”的信息增益等于 0.5000。
选择信息增益最大的 5个属性作为聚类的属性,即属性“入射功率”、“高前偏压”、“高末屏流”、“高末帘栅压”和“高末屏压”。
4.4 实验结果
在处理器是 Intel(R)Core(TM)Duo CPU T2350,主频是 1.86GHZ,内存是 2G的 PC机上,对2700条实验数据进行分析测试,参数设置如下:蚂蚁个数 =3;差异性比例因子 α=1;搜索半径 r=4;分类半径 R=3;最大迭代次数 =300000;拾起概率因子 k1=0.45;放下概率因子 k2=0.20。蚁群聚类算法运行效果如下所示:

算法总共耗时2433秒,将 2700个数据聚合成 7类,具体信息如下:第一类数据总数 240个;第二类数据总数 1364个;第三类数据总数 809个;第四类数据总数 258个;第五类数据总数 3个;第六类数据总数 3个;第七类数据总数 2个;孤立的数据总数21个。由于第五类、第六类和第七类数据数目过少,将其归为孤立的数据对象,所以数据集中分布在前四类中,分析结果也可以从图 4中直观地获得。前四类中的数据是发射机正常工作时的数据,而后三类数据和孤立的数据很可能就是故障数据,应给予重点关注。实验结果证明该蚁群聚类算法已经具备对大量数据进行聚类分析的能力。
5 结束语
本文首先论述了基本蚁群算法的原理,然后设计与实现了基于蚁堆原理的蚁群聚类算法,最后通过计算信息增益对发射机数据进行了数据降维,并对降维后的数据进行了聚类分析。通过计算属性的信息增益实现数据降维,选择较重要的属性进行聚类分析,提高了蚁群聚类算法的抗干扰能力,使聚类结果更加准确;另外降低了算法的执行时间,提高了时间效率。
[1] 段海滨.蚁群算法原理及其应用[M].北京:科学出版社,2006.1-117.
[2] 张建华,江贺,张宪超 .蚁群聚类算法综述[J].计算机工程与应用,2006,42(16):171-174.
[3] 任江涛,孙婧昊,黄焕宇,印鉴 .一种基于信息增益及遗传算法的特征选择算法[J].计算机科学,2006,33(10):52-56.
[4] 曹三省,孟静,杜怀昌,王阳 .蚁群聚类算法在 IPTV用户群偏好分析中的应用[J].中国传媒大学学报(自然科学版),2009,16(1):33-37.
[5] Dorigo M,Bonabeau E,Theraulaz G.Ant algorithms and stigmergy[J].Future Generation Computer System,2000,16(8):851-871.
[6] Colorni A,Dorigo M,Maniezzo V,etal.Distributed optimization by ant colonies[A].Proceeddings of the 1st European Conferences on Artificial Life[C].1991.134-142.
[7] CAO Sanxing,QIN Ying,LIU Jianbo,LU Rui.An ACO-based User Community Preference Clustering System for Customized Content Service in Broadband New Media Platforms[A].In Proc 2008 IEEE/WIC/ACM International Conference on Web Intelligence and Intelligent Agent Technology[C].Sydney:2008.591-595.
