3780点 FFT处理器的算法研究
2010-09-20徐晓青杨霏李建平
徐晓青,杨霏,李建平
(中国传媒大学信息工程学院,北京 100024)
1 引言
时域同步正交频分复用(TDS-OFDM)是地面数字电视标准(DMB-T)的核心技术,是属于创新的多载波调制方式。它采用 8MHz的带宽,使用3780个子载波来传输数字电视信号。TDS-OFDM技术中用于调制及解调的3780点 FFT处理器,关系到整个系统的效率和规模,是 DMB-T系统中不可缺少的重要模块之一。目前最常用的实现方法是采用层层分解的总体思想[1]:先把 3780分解为 63×60,再把 63和 60分别分解为 7×9和 3×(5×4)。综合利用混合基算法、素因子分解算法和 WFTA算法来求得 3780点的 FFT。
笔者提出一种新的分解方式,将 3780点先按素因子分解算法进行分解为 140×27,140点继续按素因子分解算法分解为 7×5×4,27点则按混合基算法分解成 3 ×9,而 9、7、5、4、3点 FFT均采用 WFTA来实现。此种分解方式在硬件实现上减少了运算量和存储空间。本论文同时对算法进行了改进,使用了同址顺序的素因子算法,省去了最后的顺序重排,且减少了存储量和数据传递次数,提高了运算速度。
2 3780点 FFT算法
2.1 混合基算法
混合基(Cooley-Tukey)的快速傅里叶算法如下:
作 N点 FFT时,如 N可分解为 N=N1×N2,且N1,N2有公共因子。
设 x(n)为 N点有限长序列,其 DFT为:

2.2 素因子算法(PFA)
利用素因子分解算法[2],旋转因子可通过选择n1,n2,k1,k2前的特殊系数而消去,于是得到 N=M1M2…Ml点 FFT
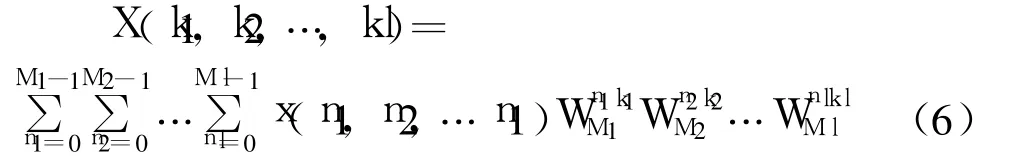
式中 M1,M2…Ml相互互质,即任意两个的最大公约数为 1,这样可把 N点的 FFT化为 l级的M1,M2…Ml点的 FFT级联来完成。算法中除了各个 Mi点的 DFT,没有引入乘旋转因子的运算,因此是一种高效的 FFT算法。
2.3 Winograd DFT algorithm(WFTA)
winograd DFT算法[3]是一种快速的短 N的 DFT算法,其核心思想是通过矩阵的降解,以实现 DFT最少的加减及乘除法运算。
N点 DFT可以用矩阵表示为 X=Wx,其中,

当 N∈{2,3,4,5,7,8,9,16}时,复数矩阵 W能够以下列方式分解:
W=ODI,
其中,D为一个 J×J的对角矩阵,并且对角线上的元素为实数或者纯虚数,O为一个 N×J的关联矩阵,I为一个 J×N的关联矩阵。与这样的W相乘可以避免复数乘法,并且加法次数与 Cooley-Tukey的算法相近,因此 winograd提出的“小 N”DFT算法是一种高效的算法。
如 N=3,WFTA如下:

可对 W进行分解,其中 O,D,I分别为:

可见总过程只需 4次实数乘法和 6次复数加法。
2.4 算法实现过程及优点
在笔者的实现方案中,素因子分解用在实现140点和 27点的 FFT上,因为 140与 27互质。140点继续按素因子分解算法分解为 7×5×4,7、5、4之间互质。由于 3与 9有公约数,所以 27则按照混合基算法分解成 3×9。而 9、7、5、4、3点 FFT均采用WFTA来实现。图 1所示为此算法结构:

图 1 3780点 FFT算法结构图
由于 140×27采用了素因子算法进行分解,因此 140点和27点 FFT之间仅存在素因子地址映射,而不存在 3780点旋转因子。但是该算法中 3×9采用的混合基算法同样存在 3780点的旋转因子,也就是说该分解方式并没有减少旋转因子的复数乘法。
经过计算发现,这种分解方式与 60×63的分解方式所需要的加法和乘法的次数是相同的。但是 3×9的混合基的旋转因子不同的只有 27个值,3780个旋转因子是 140组重复的 27个值,而 63×60的混合基的旋转因子却是 3780个不同的值。从硬件实现上面来说,明显可以看出 140×27的分解方式比 60×63的分解方式节省了复数乘法的计算量和存储空间。
2.5 算法的改进
这种分解方式也存在问题:素因子算法由于采用素因子分解,运算中省去了级间旋转因子所需的乘法,运算量小,运算速度快,但由此会导致结果数据的乱序,在输出时还要进行最后的整序工作,这一操作耗费的时间不容小视,而且增加了存储空间的开销。
于是,在研究方案中采用了同址、顺序素因子算法。它省去了最后的顺序重排,且减少了存储量和数据传递次数,提高了运算速度。
为了得到顺序的输出,而避免通过整序来对变换的结果重新排序,在一维 DFT映射成 M维 DFT时,对n和 k没有采用原先算法的下标映射关系,而是采用了相同的下标映射[4]:
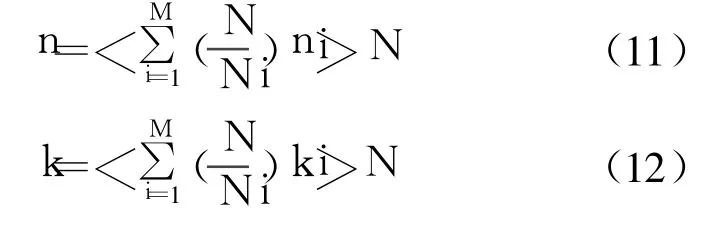
这里 <>N为模 N的意思。每个小 N点 DFT的输出都是按照 ki′进行排序的,因此要得到顺序的输出,就要按照 ki′对每个小 N点 DFT的输出重新排序。

顺序的主要思想是:WFTA小 N因子 DFT的输出按照 ki重新排序,得到的输出对 ki′是正常顺序。对每一个小 N的 DFT的重排序比较容易实现,并能节省运算量。这种算法将素因子算法最后的整序改为对每一个小 N的 DFT整序,程序仍具有通用性,而且能提高程序运行速度。
简单的说,同址运算的思想就是:对于每一个运算的输出数据,可将其存放在存储输入数据所对应的存储单元,即用输出覆盖原来的输入数据所占的RAM区域。因此值需要 N个复数的存储单元,不但可存放输入的原始数据,而且可存放中间结果,并还可以存放最后的运算结果。这种同址运算方式节省了大量的存储单元,是一大优点.
图 2为 3780点 FFT实现的流程图:

图 2 FFT实现流程图
3 结果验证
用 Matlab仿真该 FFT处理器,并与 Matlab提供的 FFT函数进行比较,可得到 FFT处理器的运算精度。输入为 3780个 16QAM的随机分布的值,图 3显示的是 matlab自带的FFT函数运行后,选取前 100个数值的显示图,而图4则是使用本文方案的算法设计后,所得结果与 matlab自带函数算出结果的差值图,从图 4中,我们可以看出,它们的差值很小,数量等级达到了 10的 -13次方,所以这种误差是可以忽略的。

4 结束语
本文介绍了一种新的 3780点 FFT处理器的算法分解方式,并采用了同址顺序的素因子算法对算法进行了改进。仿真结果表明,这种分解方式是正确的。本文介绍的分解方法,非常适用于软、硬件的实现。
[1] Zhi-Xing Yang,Yu-Peng Hu,Chang-Yong Pan,Lin Yang.Design of a 3780-point IFFT processor for TDS-OFDM[J].IEEE Tran Broadcasting,2002,48:57-61.
[2] R E布莱赫特 .数字信号处理的快速算法[M].肖先赐,等,译 .北京:科学出版社,1992.
[3] Harvey F Silverman.An Introduction to Programming the Winograd Fourier Transform Algorithm(WFTA)[J].IEEE Transactions On A-coustics,Speech,and Signal Processing,1977,25(2).
[4] Sidney Burrus C,Eschenbacher P W.An In-Place,In-Order Prime Factor FFT Algorithm[J].IEEE Transactions on Acoustics,Speech,and Signal Processing,1981,29(4).
