求极限方法研究

殷俊峰

(临沂师范学院 继续教育学院，山东 临沂 273400)

求极限方法研究

殷俊峰

(临沂师范学院 继续教育学院，山东 临沂 273400)

求极限是高等数学中最基本的运算之一，由于题型多变，所以方法灵活，技巧性强，本人根据多年的教学实践归纳概括出几种方法结合实例呈献给读者。

极限;重要极限;洛比达法则;等价无穷小

极限概念在高数的基本概念中占有重要地位。理解极限的概念，熟练掌握求极限的方法对学习高等数学有着重要的作用。

1 利用单调有界必有极限来求极限

这种方法主要用在数列极限的求解中。在求数列极限时，可以先证明其收敛，然后求出极限。例1 证明下列数列有极限并求极限

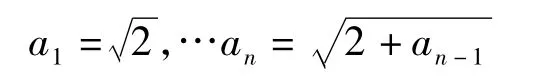
所以∀n，有an+1＞an，{an}是递增有上界数列，所以极限存在，设为a，

则有a2=2+a，解得a=2。

2 利用极限的四则运算法则求极限

四则运算法则往往用于求是有几个初等函数(极限存在)进行四则运算的情况才用它。它是由简单的函数极限计算较复杂函数的极限的理论基础。

解：当x→1时，分子、分母均趋于0，因为x≠1，约去公因子(x-1)，

此种方法是一个充分条件，运用时候需要妥善处理。

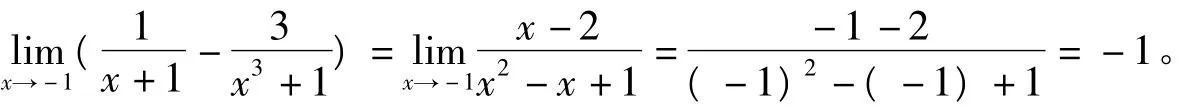
方法是固定的，运用是灵活的。

3 利用不等式即：两边夹定理求极限

4 利用变量替换求极限

解：

5 利用两个重要极限来求极限

当x→∞时u→0，

于是

两个重要极限在求极限过程中有着很重要的作用，特别要注意其变式。

6 用洛必达法则求极限

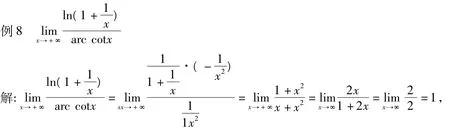
此方法运应用广泛。

7 利用定积分求极限

利用定积分求极限也是一种重要方法。定积分的本质含义是和式的极限，利用积分求解特定形式的极限问题，是微积分学的一个重要方法。

8 利用等价无穷小代换方法求极限

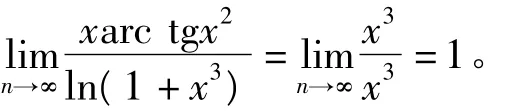
上述求极限过程使用等价的因子之间是乘积或相除的关系，等价代换可以任意使用，不会出现什么问题。但若这些因子间是相加或相减的关系，使用等价代换就会出现问题，使用时要谨慎为之。

上面对求极限的一些主要方法作了比较全面的总结，另外还有利用泰勒公式求极限，利用柯西准则求极限等方法，由于篇幅关系在此不再赘述。求极限的方法有很多，而且许多题目可以有很多种解法。极限是描述数列和函数在无限过程中的变化趋势的重要概念，是从近似认识精确，从有限认识无限，从量变认识质变的一种数学方法。同时，极限是微分的理论基础，研究函数的性质实际上就是研究各种类型的极限，如连续、导数、定积分等，由此可见极限的重要性。因此要想熟练掌握求极限的各种方法，必须通过大量的练习，在练习中体会。

解：当x→0时，ln(1+x3)～x3，arcgtx2～x2

［1］ 宋砚.求极限的常用方法［J］.内蒙古民族大学学报，2008，14(2)：4-5.

［2］ 尹国成.常见函数极限的求法［J］.保山师专学报，2009，28(2)：33-35.

［3］ 胡喜和.谈求极限的方法［J］.内蒙古电大学刊，2005(1)：108-109.

［4］ 叶志萍.洛必达法则运用中的弱点克服［J］.大连民族学院学报，2002(2)：107-110.

［5］ 程鹏.求函数极限的方法［J］.河南科技学院学报，2008，36(3)：133-135.

责任编辑：钟 声

A research on limit method

YIN Jun-feng
(Continual Education College，Linyi Normal University，Linyi 273400，China)

Calculating limit is one of the most fundamental operations.The changeable item types require us to master flexible approaches and skills.The author summaries some methods based on many years of teaching experience and presents to readers.

limit;important limit;L＇Hospital Rule;equivalent infinitesimal

O22

A

1009-3907(2010)08-0018-03

2010-06-11

殷俊峰(1978-)，男，山东费县人，讲师，硕士研究生，主要从事经济数学和运筹学方面研究。