二阶非线性耦合动力学系统守恒量的扩展Prelle-S inger求法与对称性研究

楼智美

(绍兴文理学院物理系,绍兴 312000)

二阶非线性耦合动力学系统守恒量的扩展Prelle-S inger求法与对称性研究

楼智美†

(绍兴文理学院物理系,绍兴 312000)

(2009年3月13日收到;2009年6月23日收到修改稿)

将扩展Prelle-Singer法(扩展P-S法)用于求¨x=φ1(x,y),¨y=φ2(x,y)类型的二阶非线性耦合动力学系统的守恒量,得到了积分乘子满足的微分方程与守恒量的一般形式,并讨论所得守恒量的Noether对称性与Lie对称性.最后用扩展P-S法求得了四次非谐振子系统的两个守恒量,并讨论了系统的对称性.

扩展Prelle-Singer法,二阶非线性耦合动力学系统,守恒量,对称性

PACC:0320,0230

1.引言

已知力学系统的Lagrange函数可以通过Lagrange方程求得系统的运动微分方程,且系统的运动微分方程往往是二阶非线性耦合方程,如中心力场问题、非中心力场问题和耦合谐振子等问题.寻求力学系统的守恒量一直是力学、物理学、数学研究者关注的问题,长期以来,寻找力学系统的守恒量有多种方法,如Noether对称性法[1—5]、Lie对称性法[5—7]、Mei对称性法[8—10]、Er makov方法[11—13]、Poisson括号法[14—17]、直接积分法[18—22].用Noether对称性法、Lie对称性法和Mei对称性法求守恒量都要用到群的无限小变换,理论性强且比较抽象. Ermakov方法只能求能表示成Ermakov形式系统的守恒量.Poisson括号法只能求线性耦合系统的守恒量.直接积分法用到1-形式微分式比较多,且不相互独立,导致用到的积分乘子也比较多(比扩展P-S法多2个积分乘子).近几年,数学家致力于研究用Prelle-Singer法(P-S法)求微分方程的第一积分(守恒量)[23—29].1983年,Prelle和Singer[23]提出了一种根据组成解的基本函数求得一阶微分方程解的有效方法(简称P-S法),其优点是只要一阶微分方程存在基本函数组成的解,则P-S法一定能找到其解和第一积分.P-S法求第一积分的基本思路是先假设系统存在第一积分I(守恒量),然后用几个积分乘子R,S(未知函数)去乘以恒为零的1-形式微分式,通过比较系数法求得积分乘子R,S,从而求得第一积分(守恒量).Guha等[24]将P-S法进行扩展(扩展P-S法)并应用于求解二阶及二阶以上的相互耦合的微分方程组的第一积分.而力学系统中出现的多为二阶非线性耦合的微分方程,因此,扩展P-S法可以用于求力学系统的守恒量.扩展P-S法理论简洁直观,便于掌握,便于应用.

许多力学系统的运动微分方程可以写成¨x= φ1(x,y),¨y=φ2(x,y)(不含广义速度˙x,˙y).本文将扩展P-S法应用于求二阶非线性耦合微分方程的守恒量,得到积分乘子满足的微分方程与守恒量的一般形式,并讨论所得守恒量的Noether对称性与Lie对称性.最后以四次非谐振子系统为例,用扩展P-S法求其守恒量,得到了能量积分以外的守恒量,并讨论了系统的对称性.

2.用扩展P-S法求守恒量的基本理论

在平面直角坐标系下,设力学系统的Lagrange函数为

其中m为力学系统的质量,V(x,y)为系统的势能.

则其运动微分方程可表示为

显然,φ1˙x=φ1˙y=0,φ2˙x=φ2˙y=0,这里的下标˙x,˙y表示φ1,φ2分别对˙x,˙y的偏导(本文下同).设此力学系统存在守恒量I=I(t,x,y,˙x,˙y),则

利用4个独立且恒为0的1-形式微分式:dx-˙xdt, dy-˙ydt,d˙x-φ1dt,d˙y-φ2dt.用积分乘子R1= R1(t,x,y,˙x,˙y),R2=R2(t,x,y,˙x,˙y),S1=S1(t,x,y, ˙x,˙y),S2=S2(t,x,y,˙x,˙y)分别乘以上述1-形式微分式并求和,则

令(3)与(4)式相等,并比较式中dt,dx,dy,d˙x,d˙y的系数,得

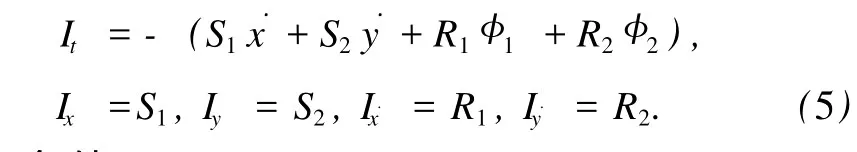
由可积条件

得

将(6c),(6d)式分别对时间求导一次,并利用(6a),(6b)式可得关于R1,R2的二阶耦合变系数微分方程组

事实上,方程(7)不封闭,无法求得其通解,只能根据研究问题的特征(是否为自治系统、Lagrange函数的形式等)先假设R1,R2的拟解,如自治系统一般可假设R1,R2不显含时间t,形如

将R1,R2及R¨1,R¨2联同(2)式代入(7)式,并比较等式两边速度项˙xm˙yn(m,n为非负整数)的系数,可得一组a1,b1,a2,b2关于x,y的偏微分方程组

先通过观察(9)式并联合(2)式,进一步假设a1,b1,a2,b2是常数或是关于x2,y2,xy等简单项的拟解,将a1,b1,a2,b2的拟解代入(9)式就可解得几组a1,b1,a2,b2的特殊解,将a1,b1,a2,b2代入(8)式就可解得几组R1,R2的特殊解.然后分别将解得的R1,R2代入(6c),(6d)式便可解得S1,S2.则守恒量的一般表达式为

将求得的每组积分乘子R1,R2,S1,S2分别代入(10)式,并设法将S1(dx-˙xdt)+S2(dy-˙ydt)+R1(d˙xφ1dt)+R2(d˙y-φ2dt)配成全微分dI(t,x,y,˙x,˙y)的形式,就可直接得到守恒量.由于R1,R2,S1,S2的解可能有多组,因此相应的守恒量也可能有多个.而求守恒量的关键是求得R1,R2.本文的第4部分中以四次非谐振子为例说明了P-S法求守恒量的过程,并得到了能量积分以外的守恒量.

3.系统的Noether对称性与Lie对称性

引进群的无限小变换

其无限小生成元向量为

(12)式的一次扩展为

二次扩展为

由Lagrange系统的Noether逆定理[1]知:如果已知Lagrange系统的α个线性独立的第一积分(守恒量)(10)式,那么可由守恒量(10)式找到相应的生成元使无限小变换(11)式为系统的Noether对称变换(或Noether准对称变换),即系统具有Noether对称性(或Noether准对称性).

对于给定的守恒量和Lagrange函数,由下面的(15),(16)式可确定生成元能使无限小变换(11)式为系统的Noether对称变换,系统具有Noether对称性.

其中~hsk(s=1,2;k=1,2)为Lagrange函数的Hess矩阵的逆矩阵.

如果由下式确定τα,有

其中Gα=Gα(t,x,y,˙x,˙y)为规范函数,且规范函数满足Noether等式

根据Lie对称性理论[1],如果由(15),(16)式或(15),(17)式确定的生成元满足下面的Lie对称性确定方程

则说明与守恒量(10)式相应的无限小变换(11)式是Lie对称变换,系统具有Lie对称性.

4.应用举例

以四次非谐振子为例说明P-S法求守恒量的过程并讨论系统的对称性.设四次非谐振子的Lagrange函数为[18]

由Lagrange方程可得系统运动微分方程为

将(21a),(21b)式代入(7a),(7b)式,得

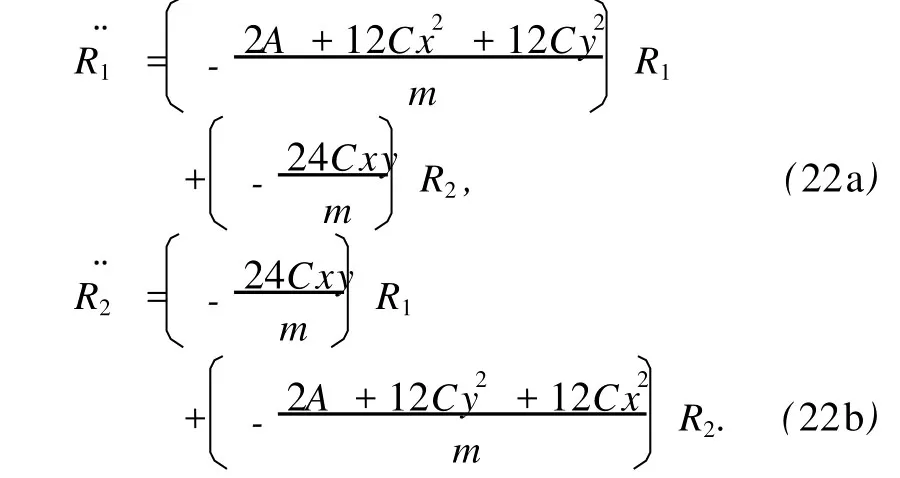
由于系统的Lagrange函数不显含时间t,且φ1(x,y), φ2(x,y)只是关于x,y的多项式,故可假设R1,R2的拟解为

将(23)式代入(22a),(22b)式可解得二组特殊解(解法如第2节所述)

将(24)式分别代入(6c),(6d)式,得

将(24),(25)式分别代入(10)式,得两守恒量

很明显,I1代表系统的能量,I2代表系统的耦合能.四次非谐振子系统具有2个守恒量,因此此系统是一可积的系统.

将(20),(26a)式分别代入(15),(16)式,可解得

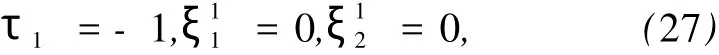
说明与守恒量I1相应的无限小变换是Noether对称变换.

将(20),(26a)式分别代入(15),(17)与(18)式,可解得

说明与守恒量I1相应的无限小变换也是Noether准对称变换.比较(27)与(28)式知,与守恒量I1相应的无限小变换是Noether对称变换,一定也是Noether准对称变换(规范函数为0).

将(26b)式代入(15)式可解得

将(20),(26b)和(29)式代入(16)式,得不到τ2的解析解,则说明不存在Noether对称变换与守恒量I2相对应.

同时考虑(17),(18),(20)及(29式,可解得

说明与守恒量I2相应的无限小变换是Noether准对称变换,而不是Noether对称变换,系统具有Noether准对称性.

下面讨论系统的Lie对称性.将(27),(30)式分别代入Lie对称性的确定方程(19),并利用(21a),(21b)式,可以证明无限小生成元(27), (30)式均满足确定方程(19),说明与守恒量I1,I2相对应的无限小变换为Lie对称变换,系统具有Lie对称性.

由(27)式知,系统的运动微分方程(21)式对于无限小变换

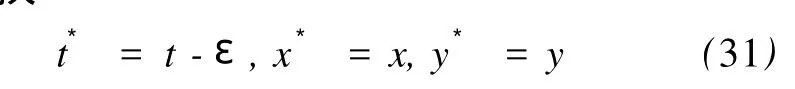
是不变的.众所周知,此变换是时间平移变换.

由(30)式知,系统的运动微分方程(21)对于无限小变换

是不变的.此变换表示时间不变,只有空间变换,且空间变换表现为x方向扩张(或收缩)与y方向的速度分量˙y有关,而y方向的扩张(或收缩)与x方向的速度分量˙x有关,即是一种与其垂直速度分量有关的空间变换,也就反映了系统的耦合性,从而导致耦合能量守恒.

5.结论

[1]Mei F X 1999Applications of Lie Groups and Lie Algebras to Constrained M echanical Systems(Beijing:Science Press)(in Chinese)[梅凤翔1999李群和李代数对约束力学系统的应用(北京:科学出版社)]

[2]ShangM,Chen XW 2006Chin.Phys.15 2788

[3]Fang J H,Liu Y K,Zhang X N 2008Chin.Phys.17 1962

[4]Fu J L,Chen L Q,Chen XW 2006Chin.Phys.15 8

[5]Luo S K 2004Acta Phys.Sin.53 5(in Chinese)[罗绍凯2004物理学报53 5]

[6]Lou ZM 2006Chin.Phys.15 891

[7]Lin P,Fang J F,Pang T 2008Chin.Phys.B 17 4361

[8]Jia L Q,Xie J F,Luo S K 2008Chin.Phys.B 17 1560

[9]Fang J H,DingN,Wang P 2007Chin.Phys.16 887

[10]GeW K 2008Acta Phys.Sin.57 6714(in Chinese)[葛伟宽2008物理学报57 6714]

[11]Haas F,Goedert J 1996J.Phys.A:M ath.Gen.29 4083

[12]Lou ZM 2005Acta Phys.Sin.54 1460(in Chinese)[楼智美2005物理学报54 1460]

[13]Lou ZM 2005Acta Phys.Sin.54 1969(in Chinese)[楼智美2005物理学报54 1969]

[14]Kaushal R S,Gupta S 2001J.Phys.A:Math.Gen.34 9879

[15]Kaushal R S,ParasharD,Gupta S 1997Ann.Phys.259 233

[16]Lou ZM 2007Chin.Phys.16 1182

[17]Lou ZM 2007Acta Phys.Sin.56 2475(in Chinese)[楼智美2007物理学报56 2475]

[18]Annamalai A,Tamizhmani K M 1994Nonlinear M ath.Phys. 1 309

[19]ShangM,Mei F X 2005Chin.Phys.14 1707

[20]Lou ZM,WangW L 2006Chin.Phys.15 895

[21]GeW K,Mei F X 2001Acta Ar mamentarii22 241(in Chinese) [葛伟宽、梅凤翔2001兵工学报22 241]

[22]Mei F X,Xie J F,Gang T Q 2007Acta Phys.Sin.56 5041(in Chinese)[梅凤翔、解加芳、冮铁强2007物理学报56 5041]

[23]PrelleM J,SingerM F 1983Trans.Amer.M ath.Soc.279 215 [24]Guha P,Choudhury A G,Khanra B 2009J.Phys.A:M ath. Theor.42 115206

[25]Duarte L G S,Duarte S E S,daMota L A C,Skea J E F 2001J. Phys.A:M ath.Gen.34 3015

[26]Duarte L G S,Duarte S E S,da Mota L A C 2002J.Phys.A: Math.Gen.35 1001

[27]Chandrasekar V K,Senthilvelan M,Lakshmanan M 2006J. Phys.A:M ath.Gen.39 L69

[28]Chandrasekar V K,Senthilvelan M,Lakshmanan M 2005J. NonlinearMath.Phys.12 184

[29]Chandrasekar V K,Senthilvelan M,Lakshmanan M 2006J. Math.Phys.47 023508

PACC:0320,0230

The extended Prelle-Singermethod for the conserved quantities of second-ordinary nonlinear coupled dynam ics system s and their symmetries

Lou Zhi-Mei†

(Department of Physics,Shaoxing University,Shaoxing312000,China) (Received 13 March 2009;revised manuscript received 23 June 2009)

The extended Prelle-Singer method is used to find the conserved quantities of second-ordinary nonlinear coupled dynamics systems such as¨x=φ1(x,y),¨y=φ2(x,y),and the differential equations of integral factors and the general expression of conserved quantities are obtained.The Noether symmetry and Lie symmetry of the systems are also discussed.Finally,two conserved quantities of quartic anharminic oscillator are obtained by the extended Prelle-Singer method,and the symmetries of this system are discussed.

extendedPrelle-Singer method,second-ordinarynonlinearcoupleddynamicssystems,conserved quantity,symmetry

†E-mail:louzhimei@zscas.edu.cn

†E-mail:louzhimei@zscas.edu.cn