Kepler方程的Noether对称性与Hoj man守恒量＊

顾书龙 张宏彬

1)(南京晓庄学院物理系,南京 211171)

2)(巢湖学院科研处,巢湖 238000)

Kepler方程的Noether对称性与Hoj man守恒量＊

顾书龙1)2)†张宏彬2)

1)(南京晓庄学院物理系,南京 211171)

2)(巢湖学院科研处,巢湖 238000)

(2009年2月5日收到;2009年5月27日收到修改稿)

研究Kepler方程的Noether对称性与Hojman守恒量.给出系统的运动微分方程并给出Noether对称性的确定方程,提出Kepler方程的Noether对称性导致的Hojman守恒量.

Kepler方程,Noether对称性,Hojman守恒量

PACC:0320

1.引言

对称性原理是近代分析力学中的一个更高层次的法则.对称性理论有许多用途,其中之一就是用来寻求守恒量.自1918年Noether[1]发表了著名的论文“Invariante Variationsprobleme”后,动力学系统的Noether对称性及其守恒量的研究取得了一系列重要成果并推广为用系统的Lie对称性、Mei对称性寻找不同的守恒量[2—4].1992年,Hojman[5]利用时间不变的无限小变换下的特殊的Lie对称性生成元直接构成动力学系统的守恒量,而无需系统的Lagrange函数和Noether等式.很快,这一方法得到迅速推广,应用到各种动力学系统[6—14].本文将研究利用时间不变的无限小变换下的Noether对称性寻找Kepler方程守恒量的间接方法.

2.平面Kepler系统的运动方程

平面Kepler系统的运动微分方程为

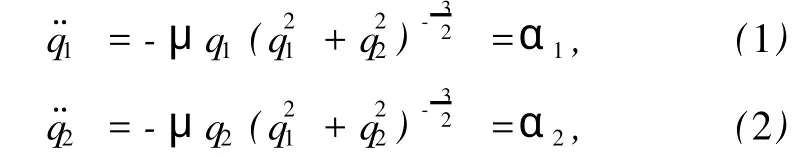
其Lagrange函数为

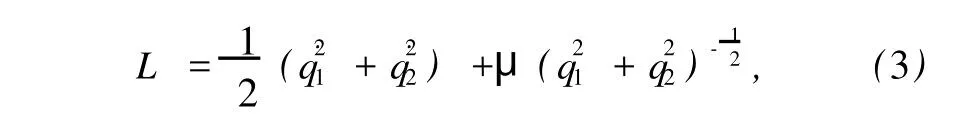
式中qs,˙qs为系统的广义坐标和广义速度,μ为常

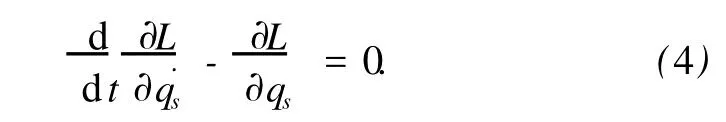
引进Euler算子

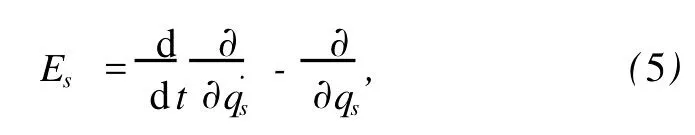
方程(4)可简写成

3.无限小变换与Noether对称性确定方程

引入时间不变的特殊的无限小变换

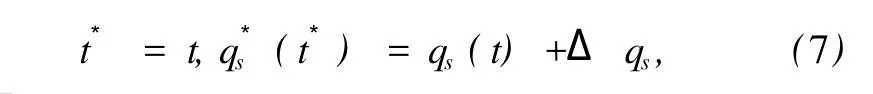
或其展开式

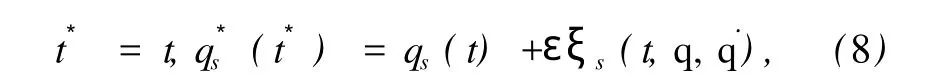
其中ε为一无限小参数,ξs为无限小生成元.

Noether对称性理论指出,对于给定的系统(3),如果存在规范函数GN=GN(t,q,˙q),使无限小变换(8)式的生成元ξs满足如下Noether对称性确定方程

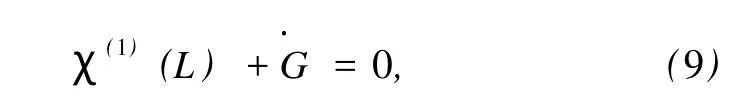
其中

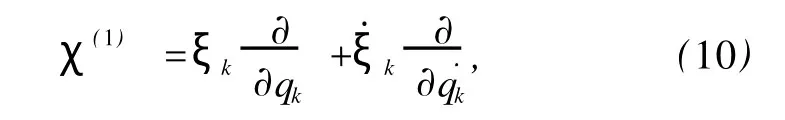
则相应的对称性为Kepler系统(1)—(3)的Noether对称性.数.系统的运动满足方程

4.Lie对称性与Hojman守恒量[1]

在变换(8)式的特殊无限小变换下,方程(1), (2)的Lie对称性确定方程为

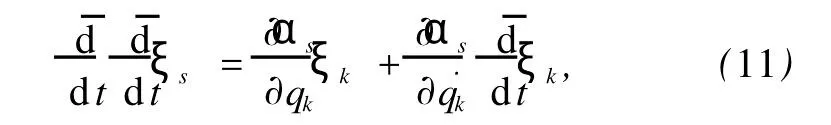
其中

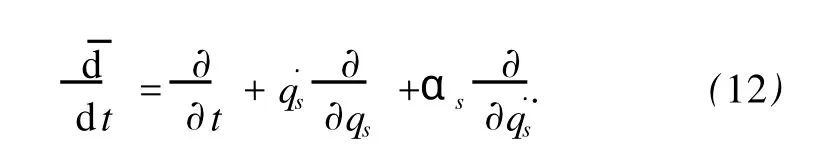
当存在函数u=u(t,q,q˙)满足

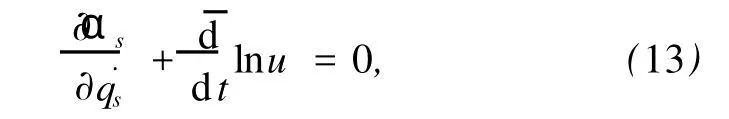
则系统的Lie对称性导致Hojman守恒量

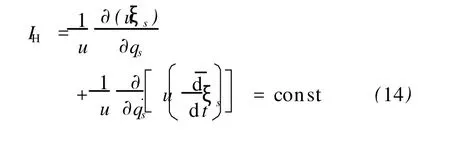
5.系统的Noether对称性导致Hojman守恒量

以下给出利用Kepler系统(1)—(3)的Noether对称性求守恒量的间接方法.

定理 对Kepler系统(1)—(3),如果Noether对称性的生成元ξs满足方程(11),且存在某函数u=u(t,q,q˙)使得(13)式成立,则Kepler系统的Noether对称性导致Hojman守恒量(14)式.

对Kepler系统,将方程(3)代入Noether等式(9)可解得

将Kepler系统的微分方程(1),(2)代入Lie对称性确定方程(11)得

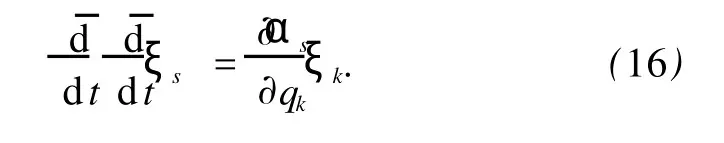
显然,Noether对称性生成元(15)满足方程(16).下面计算Kepler系统的Noether对称性导致的Hojman守恒量.

方程(13)给出

它有如下解:

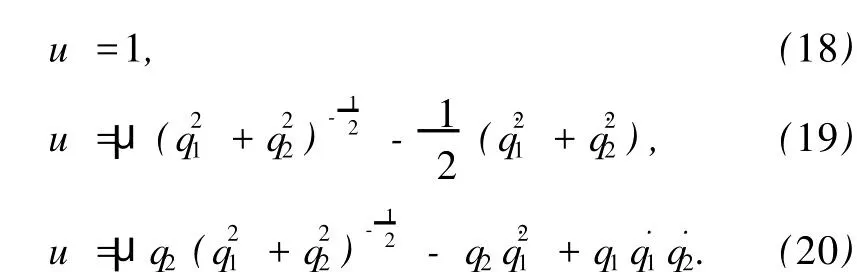
由定理,将(15)和(18)式或(19)式代入(14)式得系统的Noether对称性导致的Hojman守恒量为

它是平凡的.

若取满足(16)式的Lie对称性生成元

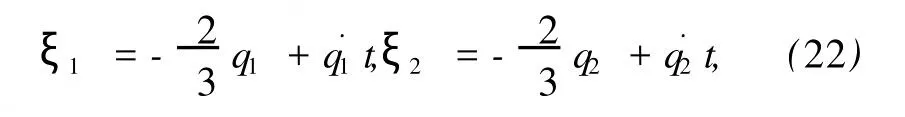
将(20)和(22)式代入(14)式得系统的Hojman守恒量为

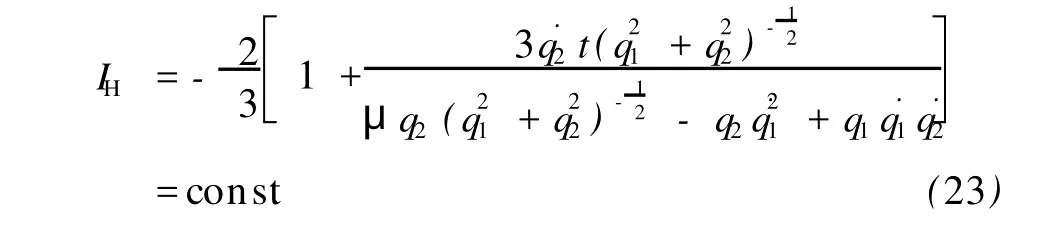
(23)式是非平凡的Ho jman守恒量.

6.结论

由动力学系统的对称性寻找守恒量的直接方法都是利用时间不变的无限小变换下的特殊的Lie对称性.本文给出了利用Noether对称性寻找Kepler方程守恒量的间接方法,即由系统的Noether对称性生成元(15)满足Lie对称性确定方程(16),可找到守恒量(23).

[1]NoetherA E 1918Nachr.Akad.W iss.M ath.Phys.2 235

[2]LutzkyM 1979J.Phys.A:Math.Gen.12 973

[3]Mei FX2004SymmetriesandConservedQuantitiesfor M echanical Systems with Constraints(Beijing:Beijing Institute Technology Press)pp12—23(in Chinese)[梅凤翔2004约束力学系统的对称性与守恒量(北京:北京理工大学出版社)第12—23页]

[4]Luo S K 2003Acta Phys.Sin.52 2941(in Chinese)[罗绍凯2003物理学报52 2941]

[5]Hojman SA 1992J.Phys.A:M ath.Gen.25 L291

[6]Zhang Y 2002Acta Phys.Sin.51 461(in Chinese)[张 毅2002物理学报51 461]

[7]DingN,Fang J H,Chen X X 2008Chin.Phys.B 17 1967

[8]Mei F X 2002Chin.Sci.Bull.47 1544(in Chinese)[梅凤翔2002科学通报47 1544]

[9]Mei F X 2003Acta Phys.Sin.52 1048(in Chinese)[梅凤翔2003物理学报52 1048]

[10]Zheng SW,Fu J L,Li X H 2005Acta Phys.Sin.54 5511(in Chinese)[郑世旺、傅景礼、李显辉2005物理学报54 5511]

[11]Gu SL,Zhang H B 2008J.AnhuiNor malUniversity31 326(in Chinese)[顾书龙、张宏彬2008安徽师范大学学报31 326]

[12]Li P,Fang J H,Pang T 2008Chin.Phys.B 17 4361

[13]Chen XW,Liu C,Mei F X 2008Chin.Phys.B 17 3180

[14]Liu C,Liu S X,Mei F X,Guo Y X 2009Chin.Phys.B 18 856

PACC:0320

Noether symmetry and the Ho jman conserved quantity of the Kepler equation＊

Gu Shu-Long1)2)†Zhang Hong-Bin2)

1)(Department of Physics,Nanjing Xiaozhuang College,Nanjing 211171,China)
2)(Department of Science and Technology,Chaohu College,Chaohu 238000,China)

5 February 2009;revised manuscript

27 May 2009)

The Noether symmetry and the Hojman conserved quantities of the Kepler equation are studied.The determining equations of Noether symmetry for the system are given.A theorem asserting that the Noether symmetry for the system leads to the Hojman conserved quantity is presented.

Kepler equation,Noether symmetry,Hojman conserved quantity

＊国家自然科学基金(批准号:10872037)资助的课题.

†E-mail:gs12142@sohu.com

＊Project supported by the NationalNatural Science Foundation of China(GrantNo.10872037).

†E-mail:gs12142@sohu.com