动力学系统Noether对称性的几何表示＊

刘 畅 赵永红 陈向炜1)(北京理工大学应用力学系,北京 100081)(商丘师范学院物理与信息工程系,商丘 476000)(商丘师范学院教务处,商丘 476000)

动力学系统Noether对称性的几何表示＊

刘 畅1)†赵永红2)陈向炜3)
1)(北京理工大学应用力学系,北京 100081)
2)(商丘师范学院物理与信息工程系,商丘 476000)
3)(商丘师范学院教务处,商丘 476000)

(2009年2月3日收到;2009年3月26日收到修改稿)

利用现代微分几何方法研究了Lagrange系统、Hamilton系统和Birkhoff系统的Noether对称性,并导出系统相应的Noether守恒量,最后给出了应用算例.

动力学系统,几何表示,Noether对称性,Noether守恒量

PACC:0320

1.引言

通过讨论动力学系统的对称性来简化系统变量的个数是研究动力学系统的一个重要主题[1—4].自Noether1918年发表不变变分问题[5]以来,Noether理论的研究引起了力学物理学和数学工作者的高度重视,并已经取得了一系列重要成果[3,6—17].文献[6]指出“Noether的结论既简单又深刻,Noether定理之完美在于它不依赖于作用量的细节,它是人类只会对自然的自信.Noether定理给数理科学带来一片光明.”近年来,国际上十分重视利用微分几何的方法来研究动力学系统的对称性与守恒量[1,18,19].利用现代微分几何理论来描述力学系统的对称性与守恒量,不仅从数学观点上提供了更为严格、简洁、优美的表达形式,而且可以直观的从全局上把握动力学系统的物理本质.

本文就是利用微分几何的方法研究了Lagrange系统、Hamilton系统和Birkhoff系统的Noether对称性,并导出相应的守恒量,最后给出了应用举例.

2.Lagrange系统的Noether对称性

2.1.Lagrange方程的几何形式

定义1 Lagrange动力学系统的状态空间为切丛流形TQ,且Lagrange函数为L:TQ|→R,在切丛流形TQ上的动力学向量场为

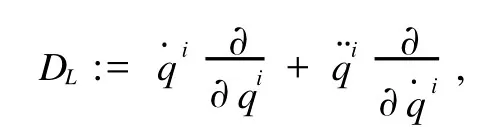
切丛流形TQ上的1-形式为

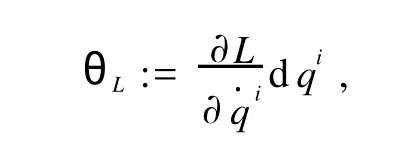
则Lagrange系统动力学方程的几何形式为

显然可证(1)式等价于通常形式的Euler-Lagrange方程[19].

2.2.Lagrange系统的Noether定理

如果Lagrange动力学系统在流ψε作用下满足

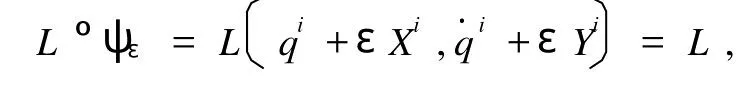
因为

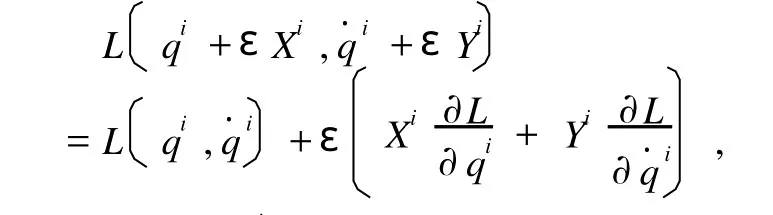
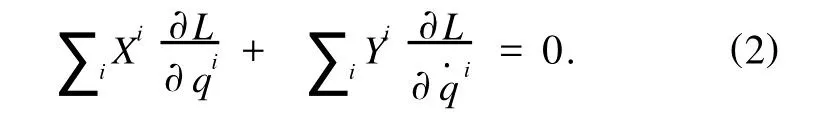
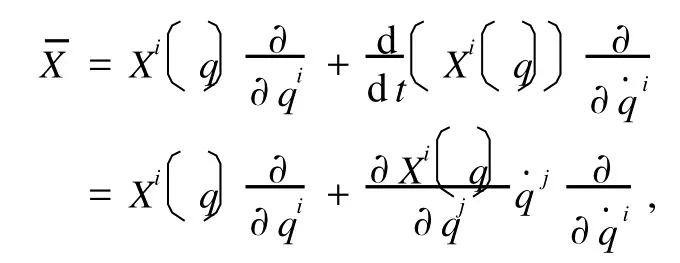
如果向量场X是Lagrange系统的Noether对称性向量场,即

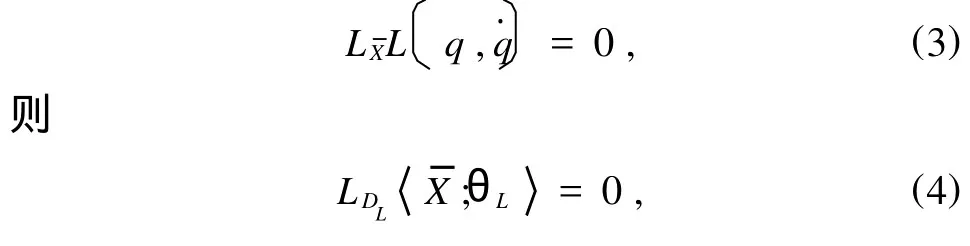
其中PX=〈¯X;θL〉为Noether守恒量.

3.Hamilton系统的Noether对称性

3.1.H amilton方程的几何形式

定义2 Hamilton动力学系统的状态空间为余切丛流形T＊Q,且Hamilton函数H:T＊Q|→R,余切丛上的动力学向量场为

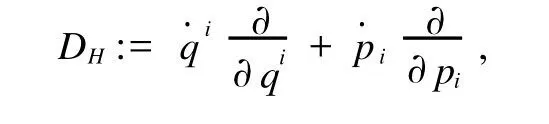
余切空间T＊Q上的1-形式为θH:=pidqi.则Hamilton系统的动力学方程可表示为

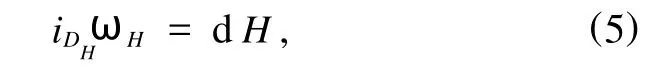
其中ωH=-dθH=dqi∧dpi.

3.2.H amilton系统的Noether定理

若向量场X是Hamilton动力学系统T＊Q,ω,H的对称性向量场,则局部存在X= Xf,并且f沿Hami-ltonian流是运动不变的.反之,如果f:T＊Q|→R是运动不变的,则Xf是Hamilton系统的对称性向量场,即

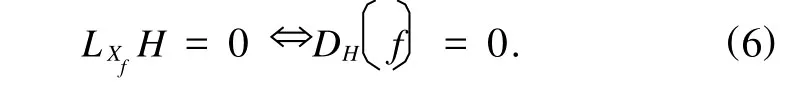
由(6)式知:

1)Hamilton系统的对称性向量场保辛结构;

2)Hamilton系统的对称性向量场保Hamilton函数不变.

4.Birkhoff系统的Noether对称性

4.1.自治Birkhoff系统的Noether对称性

自治Birkhoff系统动力学方程的几何表示为[20,21]

自治Birkhoff系统的Noether定理:若向量场Y是自治Birkhoff系统的Noether对称性向量场,则有

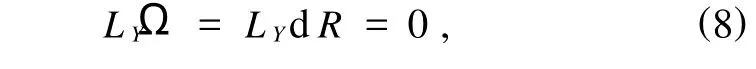
同样由(8)式可知存在函数I满足

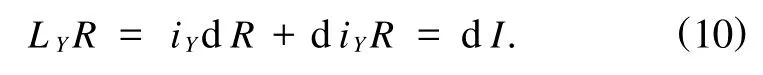
所以由(9)和(10)式可得

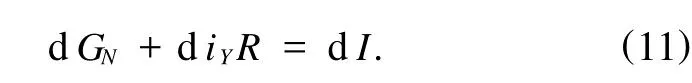
即得自治Birkhoff系统的Noether守量为

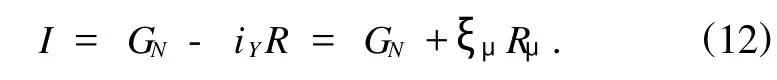
4.2.非自治Birkhoff系统的Noether对称性

非自治Birkhoff系统动力学方程的几何表示为[20,21]

非自治Birkhoff系统的Noether定理:若向量场Y是非自治Birkhoff系统的Noether对称性向量场,则有

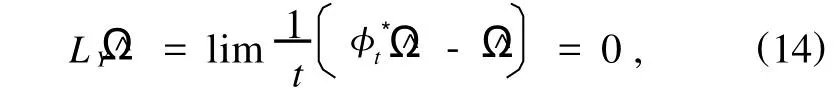
因为

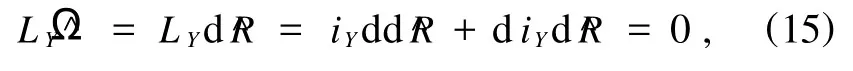
所以由Poincaré逆引理可知,存在规范函数GN满足

同样由(15)式知,一定存在函数I满足

所以由(16)和(17)式可得

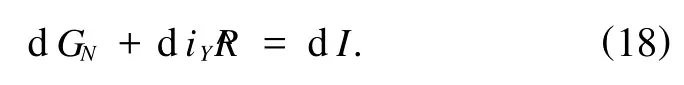
即得非自治Birkhoff系统的Noether守恒量

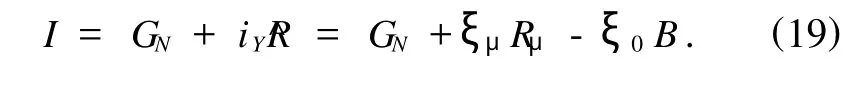
5.应用举例

例1 对于四阶自治Birkhoff系统

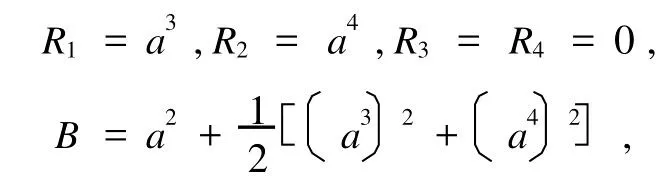
当系统的对称性群G的无限小生成元

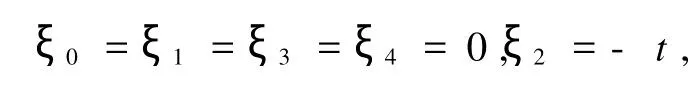
则此Birkhoff系统存在对称性向量场

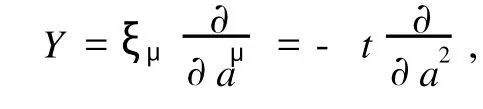
并且存在规范函数

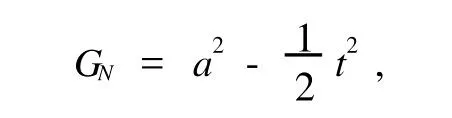
则系统存在Noether守恒量

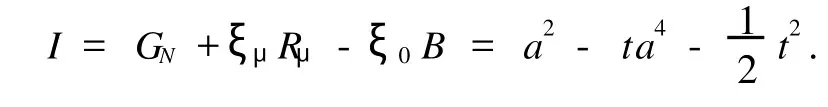
例2 对于二阶非自治Birkhoff系统

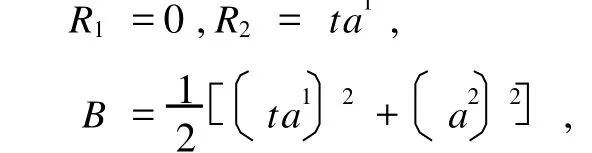
当系统的对称性群G的无限小生成元

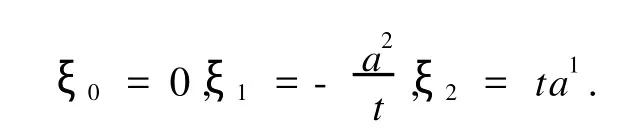
则此Birkhoff系统存在对称性向量场

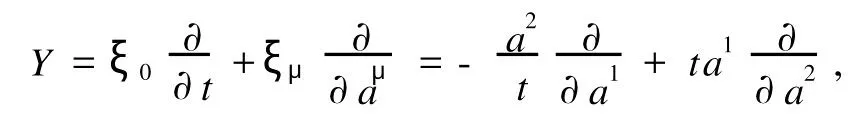
并且存在规范函数

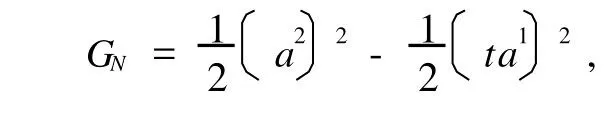
则系统存在Noether守恒量

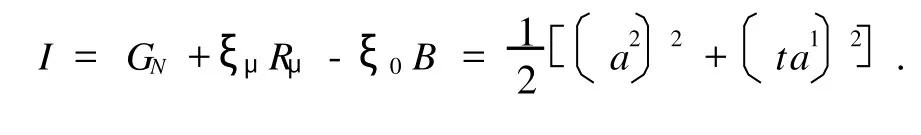
6.结论

因此利用微分几何的方法同样可以研究了Lagrange系统,Hamilton系统和Birkhoff系统的Noether对称性,并得到了相应的守恒量,形式更为简洁,而且物理意义更为明显.并且还可以

1.利用动量映射的方法研究动力学系统的Noether定理,即只要存在动力学系统的对称性群,就可以构造出Lagrange系统、Hamilton系统和Birkhoff系统的动量映射,可以证明这个动量映射函数就是系统的守恒量;

2.构造出动力学系统的动量映射以后,还可以进一步研究动力学系统的对称约化问题.

[1]Marsden JE,Ratiu T S 1999Introduction to Mechanics and Symmetry(New Y ork:Springer)2nd Edition

[2]Olver P J 2000Applications of Lie Groups to Differential Equations (New Y ork:Springer)2nd Edition

[3]Li Z P 1993Classical and Quantal Dynamics of Constrained Systems and Their Symmetrical Properties)(Beijing:Beijing Polytechnic University Press)(in Chinese)[李子平1993经典和量子约束系统及其对称性质.北京:北京工业大学出版社]

[4]Mei F X 1993 Scien.Chin.A 23 709(in Chinese)[梅凤翔1993中国科学(A辑)23 709]

[5]Noether E1918Invariance Variationsproblem.Nachr.Akad.Wiss. Göttingen.Math.Phys.1 235

[6]Zhao Y Y,Mei F X 1999Symmetries and Invariants of Mechanical Systems(Beijing:Science Press)p128-163(in Chinese)[赵跃宇、梅凤翔1999力学系统的对称性与不变量北京:科学出版社第128—163页]

[7]Mei F X 2004Symmetries and Conserved Quantities of Constrained Mechanical Systems(Beijing:Beijing Institute of Technology Press) (in Chinese)[梅凤翔2004约束力学系统的对称性与守恒量北京:北京理工大学出版社]

[8]Chen X W,Li YM 2003Chin.Phys.12 936

[9]Chen X W,Wang X M,Wang M Q 2004Chin.Phys.13 2003

[10]Chen X W,Li YM 2005Chin.Phys.14 663

[11]Mei F X,Wu H B,Zhang Y F 2006Chin.Phys.15 1932

[12]Zhang Y2006Chin.Phys.15 1935

[13]Shang M,Chen X W 2006Chin.Phys.15 2788

[14]Liu R W,Zhang H B,Chen L Q 2006Chin.Phys.15 249

[15]Xu XJ,Mei F X,Zhang Y F 2006Chin.Phys.15 19

[16]Shang M,Guo Y X,Mei F X 2007Chin.Phys.16 292

[17]Liu HJ,Fu J L,Tang Y F 2007Chin.Phys.16 599

[18]Arnold V I 1989Mathematical Methods of Classical Mechanics(New Y ork:Springer)2nd Edition

[19]JoséJ,Saletan E 1998Classical Dynamics:AContemporary Approach(Cambridge University Press)

[20]Santilli R M 1983Foundations of Theoretical MechanicsVol.Ⅱ

(Springer2Verlag,New Y ork)267

[21]Chen X W 2002Global Analysis of Birkhoffian System(Henan: Henan University Press)(in Chinese)[陈向炜2002 Birkhoff系统的全局分析(河南大学出版社)]

PACC:0320

Geometric representation of Noether symmetry for dynamical systems＊

Liu Chang1)†Zhao Y ong-Hong2)Chen Xiang-Wei3)

1)(Department of Applied Mechanics,Beijing Institute of Technology,Beijing 100081,China)
2)(Department of Physics and Information Engineering,Shangqiu Normal College,Shangqiu 476000,China)
3)(Academic Affairs Office,Shangqiu Normal College,Shangqiu 476000,China)

3 February 2009;revised manuscript

26 March 2009)

In this article Noether symmetry of Lagrange systems,Hamilton systems and Birkhoff systems are discussed by geometric methods.And the corresponding Noether conserved quantities are deduced.

dynamical systems,geometric representation,Noether symmetry,Noether conserved quantity

＊国家自然科学基金(批准号:10972127,10872084)和河南省自然科学基金(0311010900)资助的课题.

†通讯联系人.E-mail:liuchang101618@126.com

＊Project supported by the National Natural Science Foundation of China(Grant Nos.10972127,10872084),and the Natural Science Foundation of Henan Provience(Grant No.0311010900).

†Corresponding author.E-mail:liuchang101618@126.com