广义非完整力学系统的Lie对称性与Noether守恒量＊

董文山 黄宝歆

(潍坊学院物理与电子科学系,潍坊 261061)

广义非完整力学系统的Lie对称性与Noether守恒量＊

董文山†黄宝歆

(潍坊学院物理与电子科学系,潍坊 261061)

(2008年10月26日收到;2009年3月24日收到修改稿)

研究广义非完整力学系统的Lie对称性与Noether守恒量,建立Lie对称性的确定方程、限制方程和附加限制方程,给出结构方程和Noether守恒量的形式,研究Lie对称性的逆问题,并举算例说明结果的应用.

广义非完整力学,Lie对称性,守恒量

PACC:0320

1.引言

对称性原理是物理学中更高层次的法则[1],利用对称性寻求系统的守恒量是近代分析力学的重要研究方向.1979年,Lutzky[2]将Sophus Lie研究微分方程在无限小群变换下不变性的方法应用于Lanrange力学系统,得到了Noether型守恒量.其后, Lie对称性方法发展迅速,被推广到了各种力学系统,取得了一系列重要成果[1,3—15].

受有广义非完整约束的广义经典力学系统称为广义非完整力学系统.罗绍凯研究了系统的运动方程,给出了系统的Poincaré-Chetaev积分变量关系和积分不变量[16],Li等研究了广义非完整力学中奇异系统的Noether对称性[17]和Poincaré-Chetaev积分不变量[18],陈立群给出了系统的Vacco动力学方程[19],本文将对称性方法推广至广义非完整力学系统,研究系统的Lie对称性,给出系统的确定方程、结构方程和Noether守恒量的形式,最后举例说明结果的应用.

2.系统的运动微分方程

研究自由度为n的广义非完整力学系统.假设系统的位形由广义坐标qi(i=1,…,n)确定,其运动受有g个l阶线性非完整约束

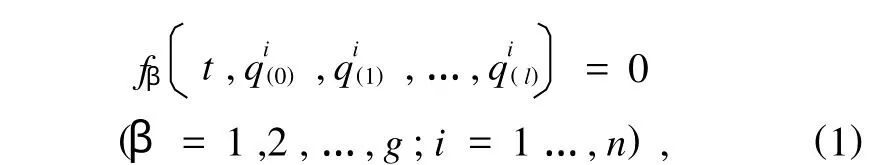
式中

在广义复合导数空间,系统的虚位移满足广义非完整力学的Ч е т а е в定义[16]

按照Lagrange乘子法,系统的Routh方程为[16]

在方程(4)积分之前,可由方程(1),(3),(4)先求出约束乘子作为的函数,于是方程(4)可表为下列相应完整系统的形式:

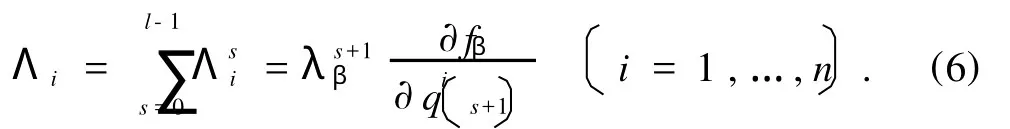
Λi为广义非完整约束反力,引入广义动量和Hamilton函数

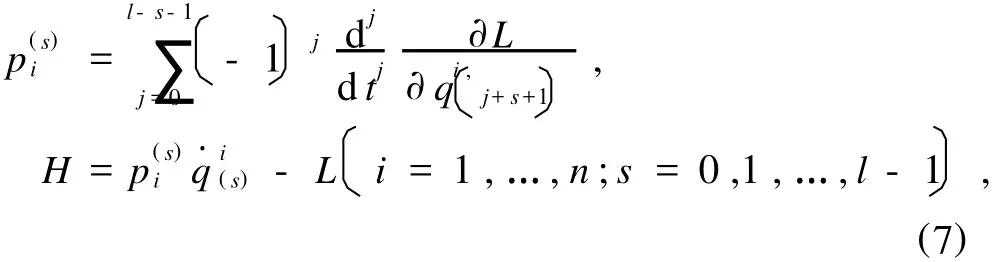
系统运动方程可表为正则形式[16]

令[20,21]

则(1),(3)式中的fβ和(8)式中~Λi可表为

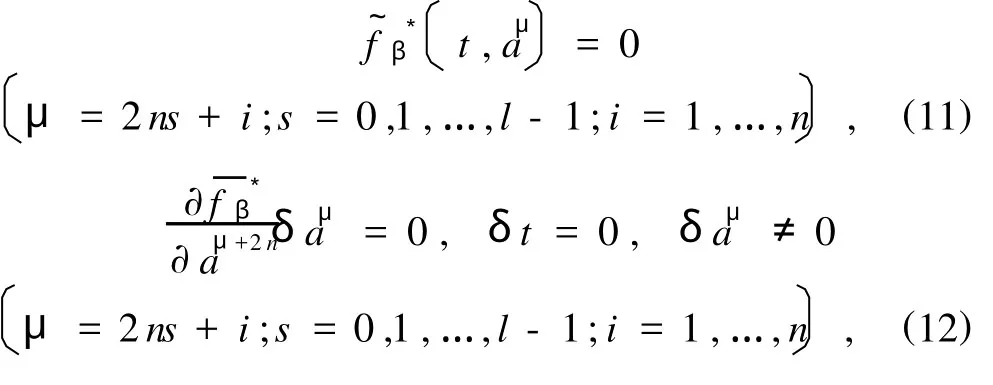
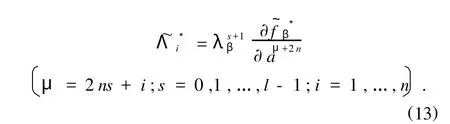
取

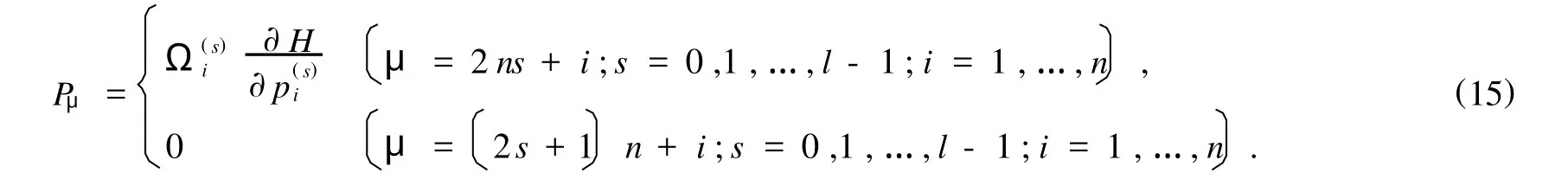
正则方程(8)可进一步表为

与(16)式相对应的逆变代数方程为

此处

其中

且

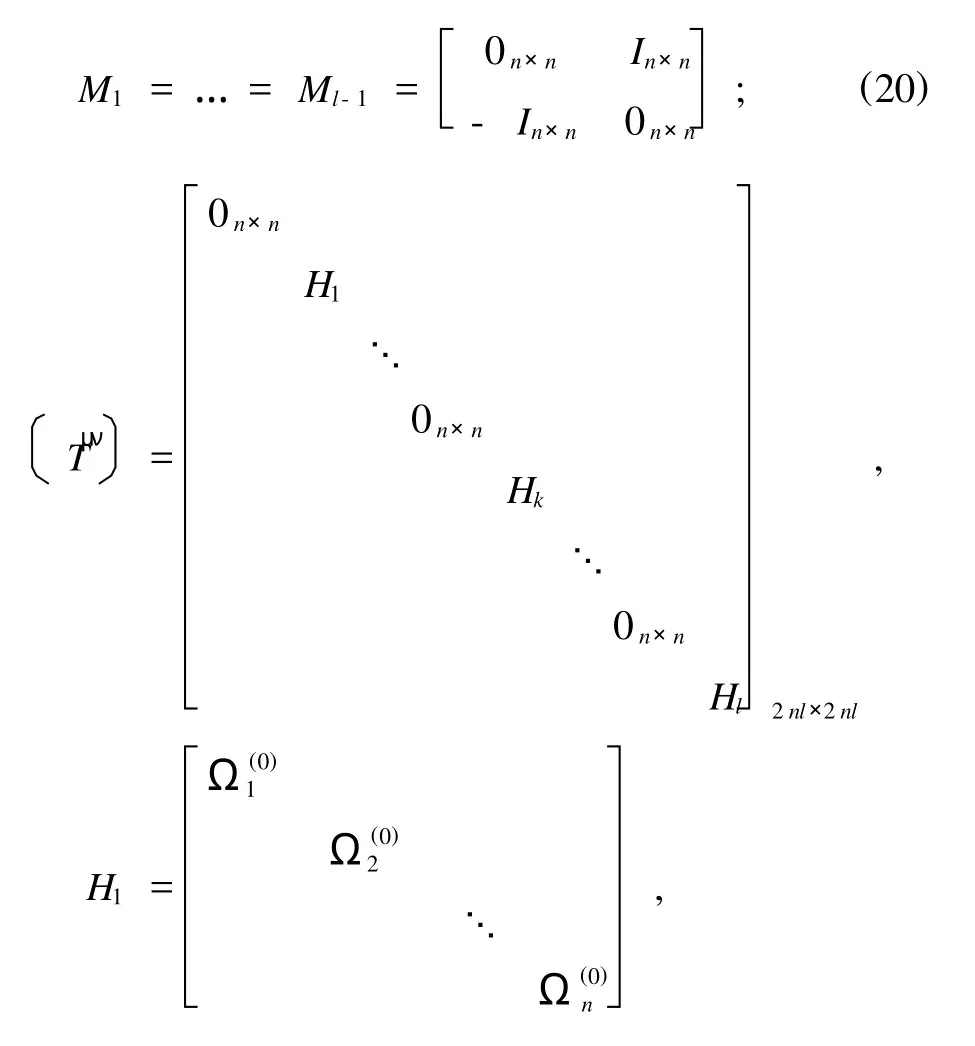
这里,0n×n是n阶零矩阵,In×n是n阶单位矩阵.因系统是非奇异的,由方程(17)可解出a·μ,记作

3.Lie对称性的判据

引进无限小单参数变换

在一级近似下,其展开式为

式中ε是无穷小参数,具有一阶小量,ξ0和ξμ为无限小单参数变换的生成元.取无限小变换的生成元向量

它的一次扩展

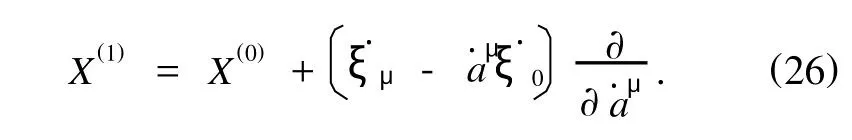
根据微分方程不变性的判据,在无穷小变换(24)式下,运动微分方程(22)的不变性归结为如下确定方程:

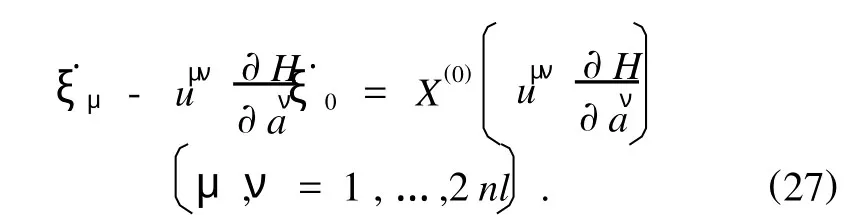
定义1 如果无限小生成元ξ0,ξμ满足确定方程(27),则称相应的对称性为与广义非完整力学系统(1),(4)相应的广义完整力学系统(6)的Lie对称性.

广义非完整约束(1)在变换(24)下的不变性归为如下限制方程:

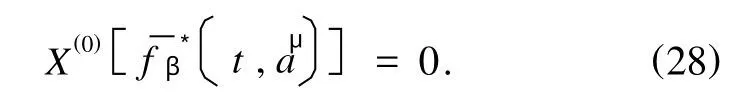
定义2 如果无限小生成元ξ0,ξμ满足确定方程(27)以及限制方程(28),则称相应的对称性为广义非完整力学系统(1),(4)的弱Lie对称性.

若考虑到广义非完整力学的Ч е т а е в定义(3)对无限小生成元ξ0,ξμ的限制,则有

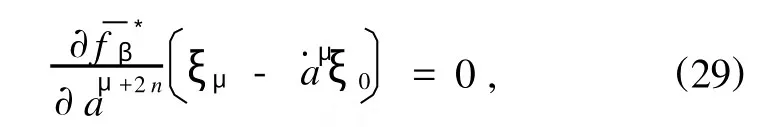
方程(29)称为附加限制方程.

定义3 如果无限小生成元ξ0,ξμ满足确定方程(27)、限制方程(28)和附加限制方程(29),则称相应的对称性为广义非完整力学系统(1),(4)的强Lie对称性.

4.系统的结构方程和Noether守恒量

对于广义非完整力学系统,Lie对称性通过Noether对称性可导致Noether守恒量.

定理1 对于广义非完整力学系统(1),(4)相应的广义完整力学系统(6),如果Lie对称性的无限小生成元ξ0,ξμ和规范函数G t,a 满足如下结构方程:

则相应的广义完整力学系统(6)的Lie对称性导致相应广义完整力学系统的Noether守恒量.

定理2 如果生成元ξ0,ξμ是广义非完整力学系统(1),(4)的弱Lie对称性生成元,且存在规范函满足结构方程(30),则广义非完整力学系统的弱Lie对称性导致相应完整系统的Noether守恒量(31).

定理3 如果生成元ξ0,ξμ是广义非完整力学系统(1),(4)的强Lie对称性生成元,且存在规范函满足结构方程(30),则广义非完整力学系统的强Lie对称性导致相应完整系统的Noether守恒量(31).

证明

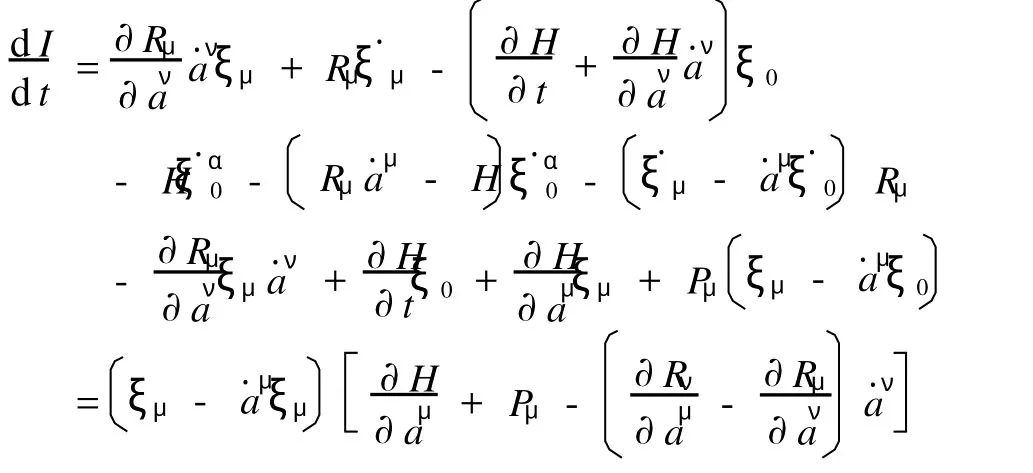
显然,系统存在守恒量(31)式.

5.系统Lie对称性的逆定理

首先由已知守恒量求出与其相应的Noether对称性.假设已知广义非完整力学系统(1),(4)有初积分

则有

将系统运动方程(16)的两端同乘以ξ—μ=ξμ-并对μ求和,得

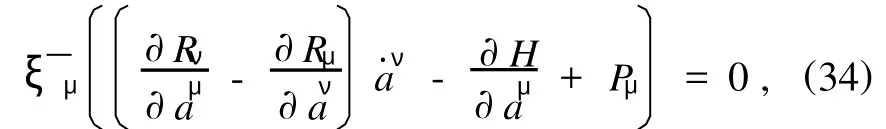
将(33)与(34)式相加后,分离出含a·ν的项,并令其系数为零,得到

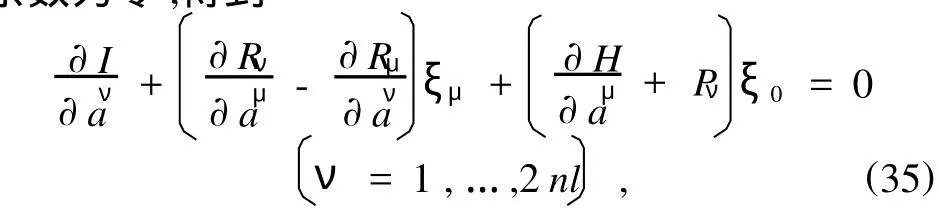
由此解得

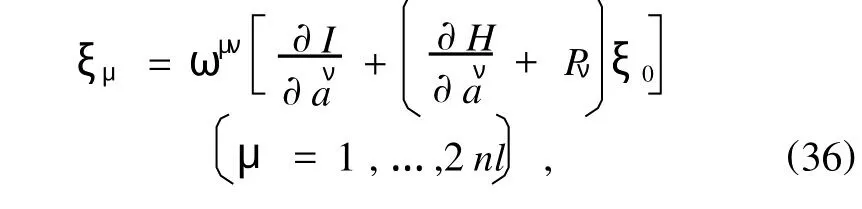
其中

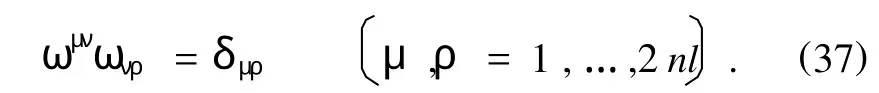
令初积分(32)式等于Lie对称性的守恒量(31)式,得

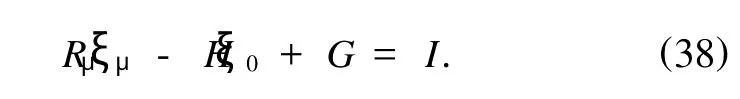
于是,在给定规范函数G的情况下,由方程(36)和(38)可求出生成元ξ0和ξμ,它们对应系统(6)的 Noether对称性.

其次,将所得对称性生成元ξ0,ξμ代入对称性确定方程(27)、限制方程(28)和附加限制方程(29),检验此对称性是否是Lie的.

定理4 如果由方程(36)和(38)确定的无限小生成元ξ0,ξμ满足确定方程(27)、限制方程(28)和附加限制方程(29),则对称性为广义非完整力学系统的强Lie对称性;如果ξ0,ξμ满足确定方程(27)、限制方程(28),则对称性为系统的弱Lie对称性;如果ξ0,ξμ仅满足确定方程(27),则对称性是相应广义完整力学系统的Lie对称性.

6.算例

设力学系统的广义Lagrange函数为

受广义非完整约束

试研究系统的Lie对称性和Noether守恒量.

首先,研究正问题.

令

系统的广义动量和Hamilton函数为

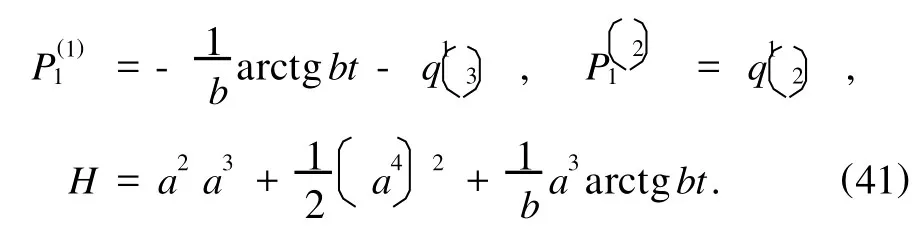
由(8),(40)和(41)式,得

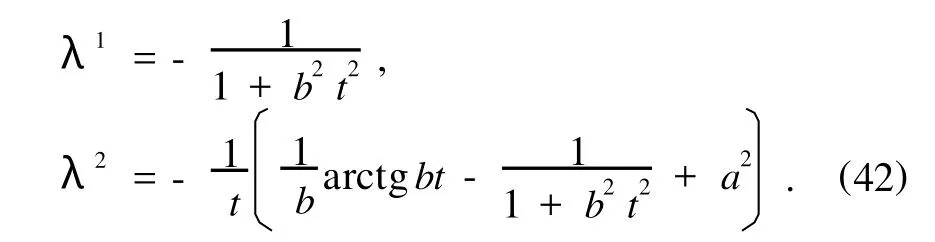
方程(17)和(18)给出Lie对称性的确定方程(27)给出

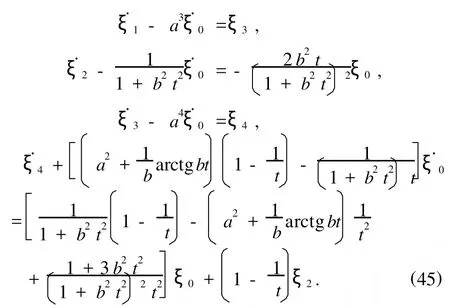
Lie对称性的限制方程(28)给出

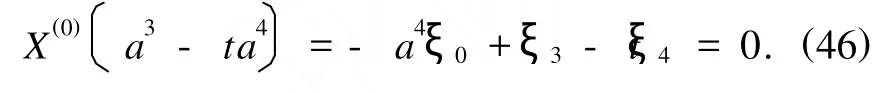
由(45),(46)式可求得如下解:

将(47)式代入结构方程(30),求得规范函数

(38)式给出系统的守恒量

其次,研究逆问题.

假设有积分(49),则由(36)和(38)两式得

当取

则有

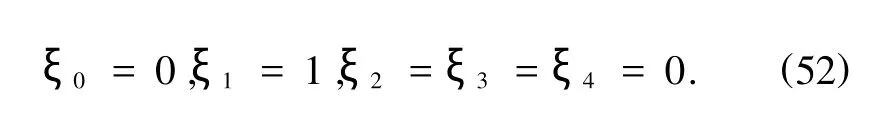
容易验证,(52)式满足确定方程(27)式和限制方程(28)式,因此,系统的对称性为弱Lie对称性.

7.结论

由于广义非完整力学系统包容了广义经典力学和一阶至高阶非完整力学,因此,本文的主要结果(27),(30)和(31)式具有普遍意义.对于不受约束的力学系统,广义非完整约束力为Λi=0,本文的结果蜕化为广义经典力学的结果[21],对于不受非完整约束的非保守力学系统,重新定义Λi为广义非势力则本文的主要结果与文献[22]的主要结果相同.

[1]Mei F X 1999Appliications of Lie Groups and Lie Algebras to Constrained Mechanical Systems(Beijing:Science Press)p1(in Chinese)[梅凤翔1999李群和李代数对约束力学系统的应用(北京:科学出版社)第1页]

[2]Lutzky M 1979J.Phys.A:Math.Gen.12 973

[3]Sen T,Tabor M 1990PhysciaD 44 313

[4]Barbara A S 1990Journal of Mathematical Physics31 1627

[5]Shivamoggi B K,Muilenburg L 1991Physics Lett.A 154 24

[6]Zhao Y Y,Mei F X 1993Advances in Mechanics23 360(in Chinese)[赵跃宇、梅凤翔1993力学进展23 360]

[7]Zhao Y Y 1994Acta Mech.Sin.26 380(in Chinese)[赵跃宇1994力学学报26 380]

[8]Mei F X 1998Chin.Sci.Bull.43 1937

[9]FangJ H,Zhao S Q 2001Acta Phys.Sin.50 390(in Chinese) [方建会、赵嵩卿2001物理学报50 390]

[10]Qao Y F,Zhao S H 20001Acta Phys.Sin.50 1(in Chinese)[乔永芬、赵淑红2001物理学报50 1]

[11]FangJ H 2002Chin.Phys.11 313

[12]Zhang H B,Gu SL 2002Chin.Phys.11 765

[13]Zhang Y2002Acta Phys.Sin.51 461(in Chinese)[张 毅2002物理学报51 461]

[14]Fu J L,Chen L Q,Bai J H,Yang X D 2003Chin.Phys.12 695

[15]Fang J H,Yan X H,Li H,Chen P S 2004Commun.Theor.Phys. 42 19

[16]Luo S K2002Acta Phys.Sin.51 1416(in Chinese)[罗绍凯2002物理学报51 1416]

[17]LiA M,JiangJ H,Li Z P 2003Chin.Phys.12 467]

[18]Li A M,Zhang Y,Li Z P 2004Acta Phys.Sin.53 2816(in Chinese)[李爱民、张 莹、李子平2004物理学报53 2816]

[19]Chen L Q1994Journal of Anshan Institute of I.&S.Technology17 29(in Chinese)[陈立群1994鞍山钢铁学院学报17 29]

[20]Zhang Y2001Acta Phys.Sin.50 2059(in Chinese)[张 毅2001物理学报50 2059]

[21]Zhang Y,Shang M,Mei F X 2000Chin.Phys.9 401

[22]Dong W S2007Journal of shandong university(Natural Science)42 30(in Chinese)[董文山2007山东大学学报42 30]

PACC:0320

Lie symmetries and Noether conserved quantities of generalized nonholonomic mechanical systems＊

Dong Wen-Shan†Huang Bao-Xin

(College of Physics and Electranic Science,Weifang University,Weifang 261061,China)

26 October 2008;revised manuscript

24 March 2009)

In this paper we study the Lie symmetries and Noether conserved quantities of generalized nonholonomic mechanical systems,and establish the determining equations,the restriction equations and the additional restriction equations.The structure equation and the formof Noether conserved quantities are obtained.The inverse problems of Lie symmetries are discussed and an example to illustrate the application of the result is given.

generalized nonholonomic mechanics,Lie symmetries,conserved quantity

＊潍坊学院自然科学基金(批准号:2008Z03)资助的课题.

†E-mail:dongwenshan@126.com.

＊Project supported by the Natural Science Foundation of Weifang University,China(Grant No.2008Z03).

†E-mail:dongwenshan@126.com.