TNT空中爆炸超压的相似律

仲 倩,王伯良,黄 菊,惠君明

(南京理工大学化工学院,江苏 南京 210094)

引 言

爆炸威力研究中,炸药爆炸产生的空气冲击波超压常常作为评价爆炸威力的一个重要参数。通常,研究人员根据实测的爆炸冲击波超压值与 TNT爆炸冲击波超压值进行比较,分别求出各对应点的等效 TNT药量,从而求出该战斗部爆炸威力 TNT当量比[1]。因此,TNT炸药爆炸冲击波超压值的准确性直接影响到战斗部爆炸威力的评估。Brode[2]及Henrych[3]等总结的超压经验公式计算结果与试验数据偏差较大,无法直接应用到战斗部威力评估中。於津[4]及杨鑫等[5]总结的经验公式精度有所提高,但由于缺乏大量的试验数据,其经验公式的适用范围较小。所以现有的TN T冲击波超压经验公式需要进一步完善。

冲击波超压测试系统的配置是影响拟合结果的一个重要因素,根据美国军用标准的要求建立了一套冲击波超压测试系,精度为 14bit,采样频率为65MHz,与以往的测压系统相比,本测试系统更加符合爆炸特性的要求[6-7]。

本研究采用该测试系统所获得数据与理论研究相结合的方法对 TNT的冲击波超压公式进行分析研究,得到 TNT爆炸冲击波超压经验公式,并将经验公式与试验数据及文献试验数据进行对比,新拟合的经验公式系统偏差较小,具有一定的适用性,为战斗部威力评估提供可靠的依据。

1 实 验

1.1 冲击波超压测试系统简介

空中爆炸超压有自由场超压和壁面超压两种。壁面超压是指初始冲击波到达壁面(主要是地面)产生反射后壁面所承受的压力,该压力比自由场压力高。由于爆炸的破坏作用等原因,要测定自由场超压很困难,尤其对于大药量试验基本上是不可能的,而且实际战斗部也是经反射后的冲击波作用毁伤目标。因此,本研究测试的是壁面压力。

根据美国军用标准和爆炸相关特性,建立了一套测试系统,如图1所示。由联动控制仪同步引爆爆源,爆源产生的冲击波经过各压力传感器的工作面时,其晶体在压力作用下发生形变,内部产生“极化现象”,在垂直于电轴的表面上产生电荷并由其内置的电荷放大器对信号进行放大,经过信号调理仪传送到多通道的VXI数据采集仪,然后由计算机系统对所获信号进行数据处理。

传感器选用美国 PCB公司 102A系列,信号调理仪选用美国 PCB公司 481A型号;数据采集仪是成都微测公司VXI-1115型,14位的精度,65M的采样率,符合美国军用标准。

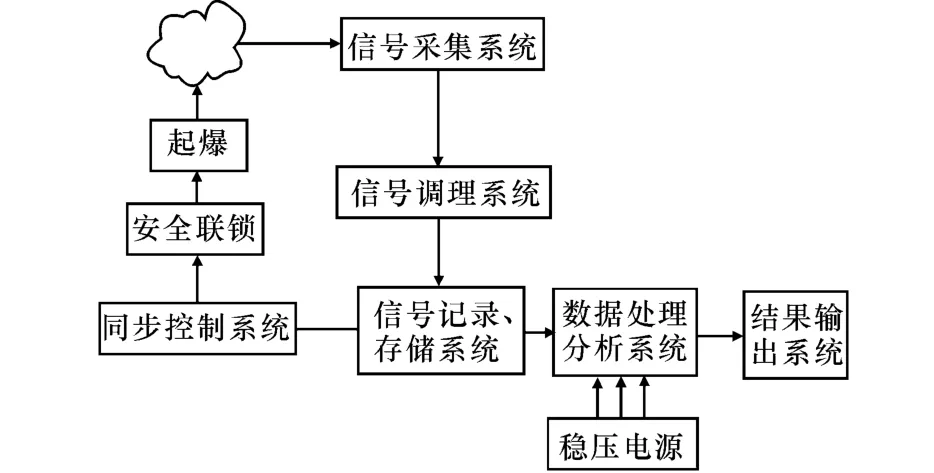
图1 测试系统示意图Fig.1 Measurement system chart

1.2 靶场布置和试验装置

将 TNT炸药放在距地面1m的支架上,以药柱在地面上的垂直投影点为爆心,在爆心相对垂直的两条射线上布置地面传感器,传感器分别布置在距爆心 3、 4、 5、 6、 8、 12、 14、 17、 20、 22和 24m 处。

1.3 样 品

试验样品为熔铸 TNT药柱,药量分别为 1、8、10、30和 35kg,装药的长径比为 1∶1,以钝化 RDX为传爆药,用 8号雷管上端起爆。

2 结果与分析

2.1 冲击波超压的经验公式

Brode[2]用模型相似理论给出 TNT爆炸冲击波峰值超压的表达式为:

式中:Δp为冲击波超压,MPa;R为比例距离(R=r/3r为测试点到爆心的距离,m;W为药量,kg)。

Henrych[3]用试验的方法得到冲击波峰值超压公式为:

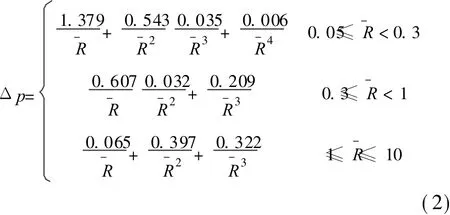
Mills用相似理论及数值模拟相结合的方法得到 TNT爆炸冲击波超压的表达式:

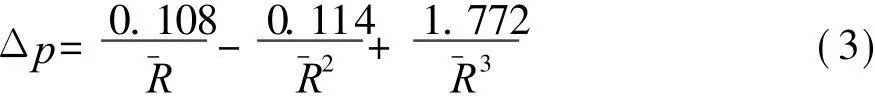
M.A.Sadovskyi[9]根据模型相似律理论建立比例距离关系比较式,由试验确定系数,得到高爆炸药冲击波峰值超压的表达式为:

对于大药量 TNT炸药爆炸,文献[10]中给出TNT在近地面爆炸时冲击波超压的计算公式:

文献[5]给出 TNT爆炸的冲击波超压计算公式:

式(6)只是对 M.A.Sadovskyi经验公式在比例距离小于 1m/kg1/3情况下的经验公式进行了修正,不具有代表性。

2.2 经验公式计算值与测试结果的对比分析

利用冲击波超压测压系统测试了两组 TNT的超压,每组试验用不同药量分别做3次平行试验。为直观地分析经验公式计算值与试验数据之间的差别,绘出不同方法计算冲击波超压比例距离的关系曲线,如图 2所示。

由图2可知,Brode和 Henrych方法的计算值偏低,Mills经验公式的计算值和文献 [5]的计算值较其他公式相对偏高,尤其是在-R 小 于 2.5m/kg1/3范围内,其计算结果与试验结果偏差较大。随着比例距离-R的 增大,经验公式的计算结果与试验数据的偏差逐渐减小,当比例距离大于3m/kg 时,两者基本比较接近。

分析认为,产生上述偏差的主要原因:一是超压峰值具有一定的离散性;二是不少研究者的实验研究进行得比较早,测试仪器相对简单,而超压峰值的获取对实验装置的灵敏度、精度及采样频率的要求都很高。

图 2 测试值与经验公式峰值超压对比Fig.2 Comparison of the measured veluesΔp with eiteratureonesΔp

因此,在本测试系统所测得数据基础上对 TNT的经验公式重新拟合,可为战斗部威力评估提供客观依据。

2.3 公式拟合

2.3.1 计算原理

根据爆炸相似规律,超压与比例距离的关系式为:

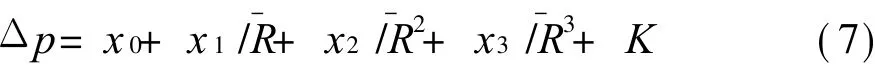
根据试验测试数据,以公式(7)为基础,运用最小二乘法原理,对 TNT进行经验公式拟合。

2.3.2 拟合公式

借助爆炸相似率和最小二乘法原理,对TNT超压测试数据进行经验公式拟合,拟合公式如下:

2.4 分析与讨论

2.4.1 相对偏差分析

经验公式的拟合过程是一个理想化的爆炸相似律的模拟,从每次测试数据来看,数据曲线并不像拟合的结果那样光滑。为验证上述拟合公式相对理论计算偏差,表 1列出了用拟合公式(8)计算的 TNT超压预测值与本次试验测试值。

从表 1可以看出,试验测试数据与公式拟合值之间的相对偏差均小于 5.30%,其绝对值的平均值为2.65%,正向偏差的平均值为6.17%,负向偏差平均值为5.62%。该公式可用于TNT冲击波超压的计算,能够满足后续的威力评价与理论分析的要求。

表 1 TNT超压值的试验数据和计算值偏差分析Table 1 Error analysis of the experimental data and caluclated ones of the TNT overpressure

2.4.2 与参考文献数据的比较

为验证上述拟合公式适用的普遍性,选取文献[11]中的 TNT实测数据带入拟合公式进行比较分析,文献[11]中的测试方法及系统配置与本研究相似,分析结果如表 2所示。

由表 2可见,文献中测试值与拟合值之间的相对偏差绝对值的平均值为5.61%,说明该拟合公式可普遍适用于 TNT冲击波超压的计算。

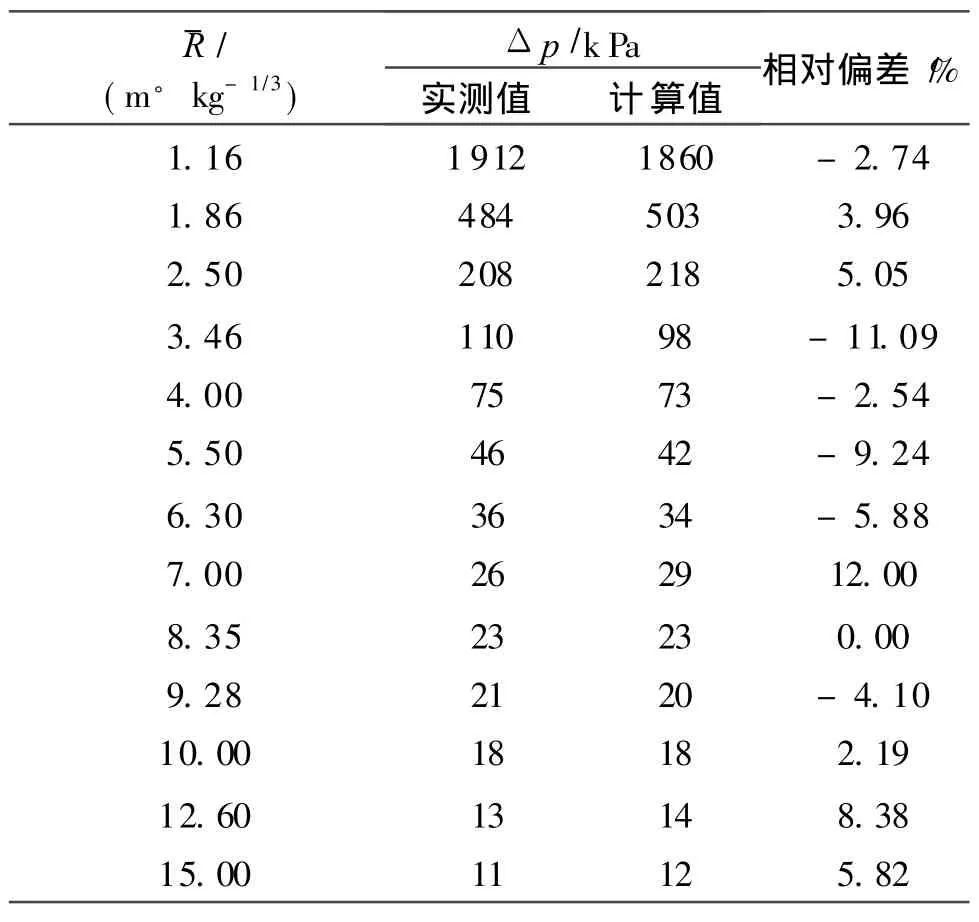
表2 与文献试验数据对比分析Table2 ComparisonoftheexperimentalvaluesΔp withtheexperimentalonesΔpinliterature

3 结 论

(1)根据美国军用标准和爆炸相关特性,建立了一套高精度和高分辨率的冲击波超压测试系统。

(2)总结出能较好描述冲击波超压峰值与对比距离相似律关系的表达式。通过与试验数据分析比较,可知该公式的预测值与试验值相对偏差均小于5.30%,其绝对值的平均值为2.65%。

(3)通过对文献试验数据与本研究表达式预测值的结果比较,其相对偏差绝对值的平均值为5.61%,表明该拟合公式可适用于TNT冲击波超压的计算。

[1] 北京工业学院八系.爆炸及其作用 (下册)[M].北京:国防工业出版社,1979.

[2] Brode H L.Blast wave from a spherical charge [J].Phys Fluids,1959(2):217.

[3] Henrych J.The Dynamics of Explosion and Its Use [M].Amsterdam:Elsevier,1979.

[4] 於津,彭金华,张陶,等.基于 MATLAB的 FAE战斗部超压计算的公式拟合 [J].弹箭与制导学报,2004,24(3):306-308.YU Jin, PENG Jin-hua,ZHANG Tao,etal.Formula fitting to overpressure calculation of FAE w arhead in MATLAB[J]. Journal of Projectiles,Rockets,Missiles and Guidance,2004,24(3):306-308.

[5] 杨鑫,石少卿.空气中 TNT爆炸冲击波超压峰值的预测及数值模拟[J].爆破,2008(2):15-19.YANG Xin,SHI Shao-qing.Forecast and simulation of peak overpressure of TNT explosion shockwave in air [J].Blasting,2008(2):15-19.

[6] 王建玲,郭炜 ,冯晓军.TNT、PBX和 Hexel空中爆炸冲击波参数的实验研究[J].火炸药学报,2008,31(6):42-44.WANG Jian-ling, GUO Wei, FENG Xiao-jun.Experimental research on the air explosion shock wave parameters of TNT,PBX and hexel[J].Chinese Journal of Explosives and Propellants,2008,31(6):42-44.

[7] Muzychuk E,May seless M,Belsky I.Influence of thepost-detonation burning process on blast wave parameters in air [C]∥22nd International Symposium on Ballistics.Canada:Destech Publications,2005:536-543.

[8] Ah med Fah my Farag Tolba.Response of FRP-Retrofitted Reinforced Concrete Panels to Blast Loading [D].Canada:Carleton University,2001.

[9] Sadovskyi M A.Mechanical action of air shock waves of explosion,based on experimental data [M].Moscow:Izd Akad Nauk SSSR,1952.

[10]惠君明,陈天云.炸药爆炸理论 [M].南京:江苏科学技术出版社,1995.

[11]张陶,惠君明.FAE爆炸场超压与威力的实验研究[J].爆炸与冲击,2004(3):176-181.ZHANG Tao,HHI Jun-ming.Experimental research on the overpressure and power in the FAEblast field [J].Explosive and Blast,2004(3):176-181.

致谢:感谢范能跃、房莹莹、王凤丹等对本实验的帮助。